НОУ ИНТУИТ | Инструктивный синтез нанометровых вычислительных структур. От элементной базы к алгоритмически ориентированным субпроцессорам.. Лекция 2: Методы оценки вычислительных характеристик задач предметной области и поддерживающих их аппаратных платформ

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 01.10.2013 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 5 студентам

| Поделиться |

Поддержать программу

Тесты AIM

Одной из независимых организаций, занимающихся оценкой производительности вычислительных систем, является компания AIM Technology [266, 301].

Компания была основана в 1981 году. Сферой ее деятельности является разработка программного обеспечения для измерения производительности вычислительных систем, а также заказное тестирование информационных систем, использующих ОС UNIX.

Используя методики оценок и тестовые смеси, разработанные AIM Technology, можно получить комплексную оценку тестируемой вычислительной системы. Вычислительная система оценивается по следующим параметрам:

Рейтинг производительности по AIM. За единицу этой величины принимается производительность эталонной вычислительной машины.
Максимальная пользовательская нагрузка. Определяет количество пользователей в системе, начиная с которого производительность системы становится меньше приемлемого уровня.
Индекс производительности утилит. Для его оценки используется тестовый пакет утилит AIM. Показывает возможности системы выполнять универсальные утилиты UNIX.
Максимальная пропускная способность. Используется для оценки производительности многопрограммных систем. Определяется как максимальное количество выполненных заданий в минуту.
Цена системы.

Тестовый набор AIM Technology - System Benchmark (Suite III) является основным тестовым набором.

С его помощью можно получить следующие оценки:

скорость обменов с оперативной памятью,
скорость вычислений с вещественными и целыми числами,
скорость выполнение обменов данными между процессорами,
скорость вызовов функций языка Си,
быстродействие операций чтения/записи на диск.

Он позволяет выполнять анализ вычислительной системы без учета работы графического интерфейса и сетевых задержек.

Компания AIM Technology предлагает специальные наборы тестовых смесей, позволяющие оценить возможности использование вычислительной системы в ряде прикладных областей:

разработка программного обеспечения;
автоматизации проектирования в машиностроении с использованием 3-мерной графики;
геоинформационные технологии;
стандартные офисные приложения (электронные таблицы, почта, текстовые редакторы);
многопользовательская среда;
среда центрального сервера для большого объема вычислений;
среда файлового сервера;
обработка транзакций в реляционной базе данных.

На основе приведенных данных можно утверждать:

современные программные инструментальные платформы, ориентированные на измерение характеристик вычислительных систем, поддерживают только процесс генерации тестов, ответственность за качество которых лежит на пользователе;
ни один программный тест не является адекватным реальному программному пакету пользователя и не отражает множество вариаций вычислительной нагрузки на компоненты исследуемой вычислительной системы;
все без исключения инженерные методики оценки производительности фактически отталкиваются от измерения времени, затраченного на решение "хорошо известной пользователю" задачи. В результате сопоставление двух ЭВМ весьма и весьма субъективно, так как и замер времени, и оценка выполненных машиной инструкций, и распределение времени между системными и прикладными задачами носят достаточно субъективный характер;
стандартные программные платформы оценки производительности и пропускной способности ЭВМ предоставляют пользователю только возможность создания тестовых программ, которые способны воспроизвести стабильную вычислительную нагрузку реальных задач только при использовании в них циклов 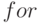, так как при использовании циклов вычислительная нагрузка зависит от содержимого преобразуемых данных;
дальнейшее развитие программных платформ оценки производительности ЭВМ, скорее всего, будет связано с созданием адаптивных средств, оперативно реагирующих и на специфику алгоритма решения задачи, и на специфику архитектуры ЭВМ, и на содержимое преобразуемых потоков данных.

1.4. Методика определения алгоритмических затрат на решение "представительных" задач, включаемых в проблемно-ориентированную инструментальную платформу оценки пропускной способности (Б)ВС

Как видно из вышеизложенного, пользователь или покупатель компьютера сам должен синтезировать тестовые программы, чтобы созданная им синтетическая смесь достоверно представляла предметную область и в полной мере проверяла структурно-функциональные возможности (Б) ВС, вычислительные алгоритмы включаемых в нее представительных задач должны обеспечить планомерные вариации нагрузки от 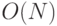O(N) до $O(N^{3})$ 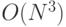на операционный, коммутационный, управляющий и диагностический ресурс, а также ресурс памяти исследуемой или испытуемой (Б)ВС.

Рассмотрим несколько алгоритмически "прозрачных" задач, позволяющих достаточно эффективно варьировать вычислительной нагрузкой в ЭВМ как последовательной, так и параллельной архитектуры.

Задача о транзитивном замыкании относится к классу типа $O(N^^{3})$ и достаточно просто приводится к параллельному виду с помощью алгоритма Уошэлла - Флойда.

Формулировка задачи. Пусть имеется ориентированный граф связности 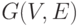G(V,E) с множеством вершин 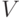и множеством ребер E. Необходимо пориен-тированный граф рис. 1.1 [70] и ему соответствует матрица смежности:

Рис. 1.1.

"Внутренний" параллелизм этой задачи в полной мере раскрывает рекурсивный алгоритм Уошэлла - Флойда [70]:

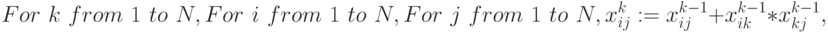$For\,\, k\,\, from\,\, 1\,\, to\,\, N, \\ For\,\, i\,\, from\,\, 1\,\, to\,\, N, \\ For\,\, j\,\, from\,\, 1\,\, to\,\, N, \\ x_{ij}^k:= x_{ij}^{k-1} + x_{ik}^{k-1} * x_{kj}^{k-1},$

( 1.1)

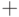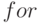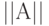где - шаг рекурсии, - логическое сложение, - логическое умножение. В этом алгоритме три вложенных цикла for , реализация которых требует $O(N^^{3})$ шагов вычисления логического выражения. Для наглядности представим матрицу ||А|| в виде таблицы, где "единичным" элементам соответствуют заштрихованные клетки, а "нулевым" - незаштри-хованные. Тогда последовательность вычислительных фаз алгоритма Уошэлла - Флойда примет вид:

Здесь пунктирными линиями показаны значения, которые пробегают индексы 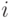и 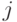на каждом шаге рекурсии .

Результирующий граф 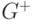$G^{+}$ имеет вид рис. 1.2, и ему соответствует матрица смежности:

Рис. 1.2.

На рис. 1.2 пунктирными стрелками показаны ребра, порождаемые на каждом шаге рекурсии, откуда видно, что шаг рекурсии соответствует номеру вершины, через которую осуществляется транзитивное замыкание с учетом предыдущих шагов рекурсии.

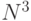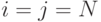Таким образом, максимальный коэффициент векторно-конвейерного распараллеливания вычислений в задаче транзитивного замыкания может достигать значения $N^{3}$ , а реально используемый зависит от структуры исходного графа и предоставляемого аппаратного ресурса. "Векторная" составляющая коэффициента распараллеливания вычислений ограничена размерами матрицы смежности ( i = j = N ) и не может превышать величины 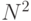$N^{2}$ , а "конвейерная" составляющая определяется индексом и не может превышать .

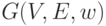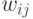Задача о кратчайшем пути аналогична задаче о транзитивном замыкании и состоит в определении кратчайшего пути между всеми парами узлов графа G(V,E,w) , где $w_{ij}$ - вес ребра, соединяющего вершину с вершиной .

В этом случае элементы матрицы 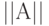||А|| определяются следующим образом:

$a_{ij}$ - расстояние из вершины в вершину , если существует ребро из в ;
$a_{ij} = \infty$ , если не существует ребра, связывающего с ;
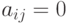$a_{ij} = 0$ , если .

Задача о кратчайшем пути заключается в вычислении матрицы 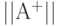$||А^{+}||$ кратчайших путей, в которых 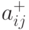$a^{+}_{ij}$ есть длина такого пути из вершины к вершине .

Например, граф связности имеет вид рис. 1.3 и ему соответствует матрица 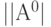$||А^{0}|$ | [70]:

Рис. 1.3.

Тогда последовательность шагов алгоритма Уошэлла - Флойда примет вид:

с той разницей, что операции 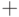соответствует выбор минимального элемента, а операции - простое сложение.

Такая представительная задача позволяет исследовать затраты на управление ходом вычислительного процесса и издержки на организацию обмена с кеш-памятью. Для этого достаточно:

в задаче о кратчайшем пути:
- с помощью датчика псевдослучайных чисел построить граф 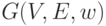и матрицу 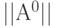$||А^{0}||$ связности целочисленных или вещественных расстояний размером ;
- принудительно присвоить диагональным элементам матрицы 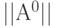$||А^{0}||$ "нулевые" значения;
- реализовать алгоритм Уошэлла - Флойда, варьируя в широких пределах, которые зависят от размеров кеш-памяти;
- построить график зависимости времени решения задачи от ;
- определить вытекающие из вычислительного алгоритма затраты на управление, пересылки данных и операционные затраты и, сравнив их с экспериментальными данными, оценить реальные системные временные издержки;
в задаче о транзитивном замыкании:
- с помощью датчика псевдослучайных чисел построить матрицу 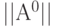связности целочисленных значений размером ;
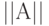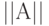- принудительно присвоить диагональным элементам матрицы "единичные" значения и с помощью варьируемого извне параметра привести матрицу к двоичному виду по правилу: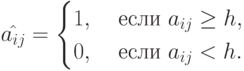
  $\hat{a_{ij}}= \begin{cases} 1, & \text{ если } a_{ij} \ge h, \\ 0, & \text{ если } a_{ij} < h. \end{cases}$
- реализовать алгоритм Уошэлла - Флойда в двух модификациях: по классической схеме и с оператором во втором цикле, благодаря которому не выполняется цикл по индексу , если $х_{ik}^{k-1}$ или $x_{ij}^{k-1}$ ; вариации осуществить в широких пределах исходя из размеров кеш-памяти;
- построить график зависимости времени решения задачи от в двух модификациях;
- определить вытекающие из вычислительных алгоритмов затраты на управление, пересылки данных и операционные затраты и, сравнив их с экспериментальными данными, оценить реальные системные временные издержки;
- вывести теоретическое условие, при котором модифицированный алгоритм должен выигрывать по времени в сравнении с классическим алгоритмом Уошэлла - Флойда и, варьируя параметром , сопоставить с реально полученными данными.

Временные затраты на управление в (1.1), то есть затраты на организацию трех вложенных цикло в 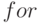for , зависят от архитектуры устройства управления процессора и в худшем случае определяются соотношением $T_{u} = (3N)^3\tau_c(p)$ , которое соответствует микропрограммному алгоритму работы простейшего целочисленного устройства управления и при условии, что команда сравнения является двухцикловой:

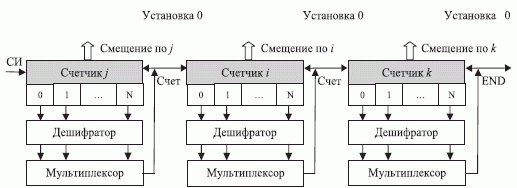
Шаг 1. Прибавить "единицу" к содержимому 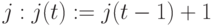j : j( t):=j(t-1)+1 .

Шаг 2. Если содержимое 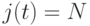j(t) = N , то прибавить "единицу" к содержимому 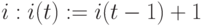i: i(t):=i(t-1)+1 и перейти к шагу 1. В противном случае выполнить шаг 1.

Шаг 3. Если содержимое 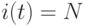i(t) = N , то прибавить "единицу" к содержимому k: k(t):=k(t-1)+1 и перейти к шагу 1. В противном случае выполнить шаг 1.

Шаг 4. Если содержимое k(t) = N , то конец программы (END). В противном случае выполнить шаг 1.

Здесь 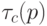$\tau_{c}(p)$ - стандартный для всех ассемблерных инструкций цикл выполнения, который задается последовательностью синхроимпульсов (СИ).

Если устройство управления процессора выполнить по схеме трехступенчатого конвейера (рис. 1.4), то временные затраты на управление станут линейными 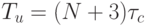$T_{u} = (N+3)\tau_{c}$ , где 3 такта задержки расходуются на "холостой ход" конвейера.

Рис. 1.4. Схема управления тремя вложенными циклами

Дальше >>

Программно-аппаратные платформы и вычислительные наноструктуры

Инструктивный синтез нанометровых вычислительных структур. От элементной базы к алгоритмически ориентированным субпроцессорам.

Методы оценки вычислительных характеристик задач предметной области и поддерживающих их аппаратных платформ

Тесты AIM

Вопросы и ответы

Студенты

Авторизоваться

Программно-аппаратные платформы и вычислительные наноструктуры

Инструктивный синтез нанометровых вычислительных структур. От элементной базы к алгоритмически ориентированным субпроцессорам.

Методы оценки вычислительных характеристик задач предметной области и поддерживающих их аппаратных платформ

Тесты AIM

Вопросы и ответы

Студенты