|
Добрый день!
Скажите, пожалуйста,планируется ли продолжение курсов по нанотехнологиям? Спасибо, Евгений
|
Методы оценки вычислительных характеристик задач предметной области и поддерживающих их аппаратных платформ
Алгоритмические временные затраты на коммутацию (пересылки данных в одноадресной ЭВМ) в (1.1) определяются организацией работы памяти. Если используется ассоциативная память (АЗУ), в которой операцию логического сложения можно выполнить непосредственным слиянием содержимого ячейки 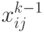 с результирующим операндом
с результирующим операндом  , то
, то  . В противном случае
. В противном случае 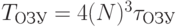 .
.
В однопроцессорных ЭВМ операционные временные затраты на (1.1) определяются соотношением  .
.
Из приведенных данных видно:
- В алгоритме Уошэлла - Флойда временные затраты на пересылки данных в 1,5-2 раза превышают затраты на обработку. Это вывод справедлив и без учета издержек на перезагрузку кеш-памяти, которая используется не только программой пользователя, но и системными программами даже в однозадачном режиме работы ЭВМ. Затраты на пересылки превосходят все остальные как за счет количества операций, так и за счет "средней" длительности каждой из них. "Средняя" длительность одной пересылки учитывает издержки на паразитное обновление кеш-памяти, и поэтому
 , и только при полном совмещении цикла обработки одной страницы кеш-памяти с циклом обновления другой ее страницы
, и только при полном совмещении цикла обработки одной страницы кеш-памяти с циклом обновления другой ее страницы  , но даже RISC -процессорах
, но даже RISC -процессорах  .
. - Из всех видов временных затрат операционные затраты алгоритма Уошэлла - Флойда, которые, собственно, только и интересуют пользователя, оказались минимальными. Полученные данные говорят о том, что при решении задач типа транзитивного замыкания в принципе невозможно получить коэффициент использования физических возможностей процессора выше 10-15 %. Попытка минимизации операционных и жестко связанных с ними коммутационных затрат приводит к включению оператора
 во второй уровень вложенности цикла
во второй уровень вложенности цикла 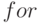 и при наличии оптимизирующего компилятора это выполняется автоматически:
и при наличии оптимизирующего компилятора это выполняется автоматически:
( 1.2) 
( 1.3)
В вычислительном алгоритме (1.2) экономия от включения цикла  зависит от количества элементов матрицы смежности
зависит от количества элементов матрицы смежности  с "нулевыми" значениями, а в (1.3) - от количества элементов с "единичными" значениями, которое возрастает с ростом индекса
с "нулевыми" значениями, а в (1.3) - от количества элементов с "единичными" значениями, которое возрастает с ростом индекса  . Поэтому по мере роста индекса
. Поэтому по мере роста индекса  в случае (1.2) экономия от включения цикла
в случае (1.2) экономия от включения цикла  будет падать, а в случае (1.3) - возрастать, но в любом случае затраты на управление увеличатся на
будет падать, а в случае (1.3) - возрастать, но в любом случае затраты на управление увеличатся на  .
.
Отсюда, в "пользовательском" варианте предпочтение следует отдавать вычислительному алгоритму по варианту (1.3), но в синтетические и испытательные программы для полноты эксперимента необходимо включать все три варианта, так как они моделируют различные условия (не) зависимости временных затрат от содержимого преобразуемых данных.
Алгоритм Уошэлла - Флойда допускает только ОКМД-режим распараллеливания вычислений как по векторной, так и по конвейерной составляющей с коэффициентами  и
и  соответственно. Приведенные данные говорят о том, что минимально возможное время
соответственно. Приведенные данные говорят о том, что минимально возможное время  решения задачи транзитивного замыкания по классическому алгоритму Уошэлла - Флойда можно получить в специализированной параллельной архитектуре с максимальным коэффициентом векторно-конвейерного распараллеливания
решения задачи транзитивного замыкания по классическому алгоритму Уошэлла - Флойда можно получить в специализированной параллельной архитектуре с максимальным коэффициентом векторно-конвейерного распараллеливания  , который поддерживается полнодоступным ассоциативным ЗУ на
, который поддерживается полнодоступным ассоциативным ЗУ на 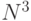 портов и
портов и 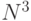 операционными устройствами, осуществляющими обмен данными с каждым портом ассоциативного ЗУ по двум входным и одной выходной однобитной шине данных. Во всех остальных архитектурах время решения за
дачи лимитируется характеристиками ОЗУ, поддерживающими соответствующий коэффициент распараллеливания вычислений по потокам данных:
операционными устройствами, осуществляющими обмен данными с каждым портом ассоциативного ЗУ по двум входным и одной выходной однобитной шине данных. Во всех остальных архитектурах время решения за
дачи лимитируется характеристиками ОЗУ, поддерживающими соответствующий коэффициент распараллеливания вычислений по потокам данных:  .
.
Задачи векторно-матричной алгебры перекрывают весь спектр размерностей задач табл. 1.1:
-
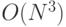 , если выполняется умножение матриц
, если выполняется умножение матриц  ;
; -
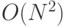 , если выполняется умножение векторов
, если выполняется умножение векторов  ;
; -
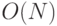 , если выполняется сложение двух векторов
, если выполняется сложение двух векторов  .
.
Поэтому эти задачи стараются включать во все испытательные и синтетические программы для оценки пропускной способности ВС по потокам команд и данных практически всех параллельных архитектур.
При всей кажущейся простоте исходного алгоритма умножения матриц, его можно реализовать тремя типами вычислительных алгоритмов, отличающимися порядком формирования результирующей матрицы.
- Вычислительный алгоритм умножения матриц с поэлементным
порядком формирования результирующей матрицы:

- Вычислительный алгоритм умножения матриц с "построчным"
порядком формирования результирующей матрицы:

где
 ,
, 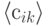 - соответственно строки матриц
- соответственно строки матриц  и
и 
- Вычислительный алгоритм умножения матриц с порядком формиро
вания результирующей матрицы "по столбцам":

где
 ,
, 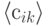 - соответственно строки матриц
- соответственно строки матриц  и
и 
Изменение порядка формирования результирующей матрицы сопровождается изменением порядка вызова данных, который может либо совпадать, либо не совпадать с порядком их хранения в ОЗУ. В современных ЭВМ данные в ОЗУ чаще хранятся по строкам и реже по столбцам. Это значит, что при "чтении" данных по столбцам и больших размерах преобразуемых матриц, превышающих размеры доступной пользователю кеш-памяти, возрастают паразитные пересылки страниц между кеш-памятью и ОЗУ и, как следствие, увеличивается продолжительность "среднего" цикла обращения к памяти.
Поэтому с помощью такой представительной задачи можно исследовать издержки на организацию обмена с кеш-памятью, для чего достаточно:
- с помощью датчика псевдослучайных чисел построить матрицы
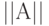 и
и  размером
размером  ;
; - реализовать алгоритмы поэлементного, "построчного" и "постолбцового" порядков формирования результирующей матрицы
 , изменяя
, изменяя  в широких пределах, зависящих от размеров кеш-памяти;
в широких пределах, зависящих от размеров кеш-памяти; - выполнить транспонирование матрицы
 после поэлементного ее формирования и определить временные затраты;
после поэлементного ее формирования и определить временные затраты; - реализовать постолбцовое формирование матрицы
 с "построчным" порядком записи ее элементов;
с "построчным" порядком записи ее элементов; - определить вытекающие из каждого вычислительного алгоритма затраты на управление, пересылки данных и операционные затраты и сравнить их с экспериментальными данными.
Временные затраты на управление в задачах векторно-матричной алгебры аналогичны затратам задачи о транзитивном замыкании и в зависимости от архитектуры устройства управления процессора могут составлять либо  , либо
, либо  .
.
Операционные временные затраты в данном случае зависят от схемы распараллеливания и не зависят от вычислительного алгоритма. Поэтому имеет смысл говорить только об удельных операционных затратах на формирование одного элемента результирующей матрицы, так как общее время вычисления всех ее элементов определяется доступным пользователю коэффициентом распараллеливания.
В изделиях микроэлектроники наибольшее распространение получили две схемы векторно-конвейерного распараллеливания ОКМД-типа на основе коллективов "скаляторных" операционных устройств, каждое из которых представляет последовательно соединенные умножитель на два входа и сумматор (рис. 1.5).
Продолжительность  цикла формирования элемента
цикла формирования элемента 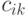 , результирующей матрицы схемы рис. 1.5-а более чем в 2 раза может превосходить продолжительность
, результирующей матрицы схемы рис. 1.5-а более чем в 2 раза может превосходить продолжительность  того же цикла схемы рис. 1.5-б. В первом случае темп работы двухступенчатого конвейера из умножителя и сумматора-накопителя регламентирует более медленный умножитель, а во втором случае фаза умножения выполняется по всем входным операндам одновременно и поэтому темп работы
того же цикла схемы рис. 1.5-б. В первом случае темп работы двухступенчатого конвейера из умножителя и сумматора-накопителя регламентирует более медленный умножитель, а во втором случае фаза умножения выполняется по всем входным операндам одновременно и поэтому темп работы  ступенчатого конвейера лимитирует только фаза суммирования. Но это справедливо для (полу)заказного исполнения "скаляторов", в рамках которого справедливо неравенство
ступенчатого конвейера лимитирует только фаза суммирования. Но это справедливо для (полу)заказного исполнения "скаляторов", в рамках которого справедливо неравенство  , где
, где  и
и  - соответственно достижимое время
цикла срабатывания аппаратно реализованного умножителя и сумматора. В RISC -архитектурах по определению
- соответственно достижимое время
цикла срабатывания аппаратно реализованного умножителя и сумматора. В RISC -архитектурах по определению  и темп вычисления элемента результирующей матрицы по схеме рис. 1.5-б определяется соотношением
и темп вычисления элемента результирующей матрицы по схеме рис. 1.5-б определяется соотношением 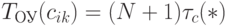 .
.
В любом случае такой выигрыш оплачивается практически TV -кратным увеличением аппаратных затрат на схему рис. 1.5-б. Поэтому на практике большее распространение получила схема рис. 1.5-а, на основе которой можно варьировать коэффициентом распараллеливания  в пределах
в пределах 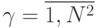 , а не
, а не  .
.
При вычислении одного элемента результирующей матрицы на одном "скаляторном" устройстве рис. 1.5-а удельные алгоритмические временные затраты на коммутацию (пересылки данных в одноадресной ЭВМ) для всех трех алгоритмов определяются соотношением  . Снизить эти затраты можно в схеме "скалятора" с
. Снизить эти затраты можно в схеме "скалятора" с  аккумуляторами, образующими FIFO -регистровую цепочку. Для такой схемы
аккумуляторами, образующими FIFO -регистровую цепочку. Для такой схемы  (рис. 1.6).
(рис. 1.6).
"Скалятор" с  аккумуляторами наиболее эффективен при построчном формировании элементов результирующей матрицы, так как в этом случае:
аккумуляторами наиболее эффективен при построчном формировании элементов результирующей матрицы, так как в этом случае:
- элемент
 вызывается один раз и хранится в регистре умножителя в течение всего времени обработки строки
вызывается один раз и хранится в регистре умножителя в течение всего времени обработки строки 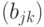 ;
; - построчный порядок "чтения" элементов обеих матриц
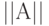 и
и  совпадает с порядком их хранения в ОЗУ, что минимизирует количество паразитных перезагрузок кеш-памяти при "больших" размерах этих матриц.
совпадает с порядком их хранения в ОЗУ, что минимизирует количество паразитных перезагрузок кеш-памяти при "больших" размерах этих матриц.
Однако такой двукратный выигрыш во времени оплачивается  -кратным ростом аппаратных затрат на FIFO -регистровую цепочку аккумуляторов.
-кратным ростом аппаратных затрат на FIFO -регистровую цепочку аккумуляторов.
Из приведенных данных видно, что эффективное совмещение обработки одной области кеш-памяти с обновлением другой ее области можно получить, если  , что осуществимо, если
, что осуществимо, если  . Последние условие как раз и предполагает отсутствие паразитных обновлений кеш-памяти за период вычисления матрицы
. Последние условие как раз и предполагает отсутствие паразитных обновлений кеш-памяти за период вычисления матрицы  .
.
Таким образом, включив в состав синтетических и испытательных программ все три варианта вычислительных алгоритмов умножения матриц, можно с различной степенью интенсивности симулировать паразитные обновления кеш-памяти по ходу вычислений. Это позволяет при одних и тех же исходных данных в процессе испытаний и исследований (Б)ВС варьировать общим временем решения задач векторно-матричной алгебры в пределах 20-40 %.
Как показали эмпирические данные, в пользовательскую библиотеку вычислительных алгоритмов векторно-матричной алгебры, содержащую подпрограммы поэлементного умножения матриц и транспонирования, имеет смысл включить подпрограмму построчного умножения, что улучшает качество работы всего пакета на 20-30 %.
Задача сортировки данных методом "пузырька" относится к классу задач типа  , и при ее распараллеливании возникают достаточно типичные издержки управления коллективом вычислителей, которые связаны с информационной зависимостью параллельных процессов и которые кардинальным образом снижают фактический коэффициент распараллеливания.
, и при ее распараллеливании возникают достаточно типичные издержки управления коллективом вычислителей, которые связаны с информационной зависимостью параллельных процессов и которые кардинальным образом снижают фактический коэффициент распараллеливания.
Алгоритм сортировки методом "пузырька":

где  представляет собой транспозицию (перестановку) сравниваемых элементов
представляет собой транспозицию (перестановку) сравниваемых элементов  и
и  .
.
Чтобы исследовать издержки управления сортировкой данных методом "пузырька", связанные с ростом коэффициента распараллеливания вычислений, достаточно:
- С помощью датчика псевдослучайных чисел построить последовательность чисел
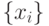 мощности
мощности  .
. - Упорядочить по возрастанию последовательность
 методом "пузырька" и подсчитать количество выполненных транспозиций
методом "пузырька" и подсчитать количество выполненных транспозиций  .
. - Разбить последовательность
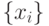 на две равные части:
на две равные части:  и повторить шаг 2 для каждой последовательности
и повторить шаг 2 для каждой последовательности  и
и  , подсчитав
, подсчитав  и
и 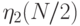 . Выбрать и запомнить
. Выбрать и запомнить ![\max[\eta_1(N/2), \eta_2(N/2)]](/sites/default/files/tex_cache/114613ad9b4c99dc84b07bd4291ccff0.png) .
. - Сравнить "старший" элемент упорядоченной последовательности
 с младшим" элементом последовательности
с младшим" элементом последовательности  и при необходимости выполнить транспозицию, переводящую элемент
и при необходимости выполнить транспозицию, переводящую элемент  и элемент
и элемент  .
. - Упорядочить модифицированные последовательности
 и
и  и определить
и определить ![\max[\eta_1(N/2), \eta_2(N/2)]](/sites/default/files/tex_cache/114613ad9b4c99dc84b07bd4291ccff0.png) . Запомнить сумму
. Запомнить сумму ![\eta(N_1,N_2)=\max[\eta_{1}(N/2), \eta_{2} (N/2)]+\max[\eta_{12} (N/2), \eta_{21} (N/2)]](/sites/default/files/tex_cache/3fb7f64d739c598464c4840e3e3de13a.png) .
. - Шаги 4 и 5 повторять до тех пор, пока
 .
. - Шаги 3-6 повторить для
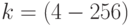 , где
, где  - коэффициент распараллеливания алгоритма сортировки данных.
- коэффициент распараллеливания алгоритма сортировки данных.
Условие останова алгоритма сформулировано в шестом пункте, из чего следует, что его размерность нарастает по  . Это условие представляет простейший алгоритм управления многопроцессорной системой, в которой согласно условию четвертого шага запуск следующей итерации многопроцессорной сортировки осуществляется синхронно и синфазно по всем процессорам и после того, как завершил работу самый нагруженный из них. Возникающие при этом "простои" процессоров накапливаются в сумме
. Это условие представляет простейший алгоритм управления многопроцессорной системой, в которой согласно условию четвертого шага запуск следующей итерации многопроцессорной сортировки осуществляется синхронно и синфазно по всем процессорам и после того, как завершил работу самый нагруженный из них. Возникающие при этом "простои" процессоров накапливаются в сумме  , которая вычисляется на пятом шаге. Поэтому отношение
, которая вычисляется на пятом шаге. Поэтому отношение  характеризует реально полученный "средний" коэффициент распараллеливания вычислений, так как "объем выполненной работы" (число транспозиций) и в однопроцессорном, и в многопроцессорном вариантах один и тот же.
характеризует реально полученный "средний" коэффициент распараллеливания вычислений, так как "объем выполненной работы" (число транспозиций) и в однопроцессорном, и в многопроцессорном вариантах один и тот же.
Эмпирические данные говорят о том, что начиная с  один и более процессоров гарантировано начинают работать "вхолостую" и их количество возрастает с ростом
один и более процессоров гарантировано начинают работать "вхолостую" и их количество возрастает с ростом  до такой степени, что делает бессмысленным наращивание аппаратной платформы уже при
до такой степени, что делает бессмысленным наращивание аппаратной платформы уже при  .
.
В таких условиях можно варьировать правилами останова, что позволяет симулировать тот или иной вариант управления многопроцессорной архитектурой: распределенной, централизованной, потоком данных и т. п., который призван минимизировать простои базового алгоритма управления.
Таким образом, "представительность" задач сортировки состоит в том, что они позволяют исследовать пропускную способность сильно связанных многопроцессорных систем, не усложняя при этом вычислительное ядро алгоритма.
Одним из главных ограничивающих коэффициент распараллеливания факторов связан с падением вычислительной устойчивости алгоритмов при их реализации на параллельных архитектурах (см. раздел 6.6 курса "Задачи и модели вычислительных наноструктур"). Поэтому одна из главных задач исследований и испытаний параллельных (Б)ВС состоит в том, чтобы определить вычислительную устойчивость всех решаемых задач.
В вычислительной технике алгоритм и реализующая его программа считаются вычислительно устойчивыми, если погрешность вычисления результата не превосходит погрешности представления исходных данных.
Методику исследования вычислительной устойчивости алгоритмов проще всего проиллюстрировать на примере программы суммирования членов псевдослучайной последовательности из  элементов.
элементов.


