|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
Машинное обучение
Презентацию к лекции Вы можете скачать здесь.
Дополнительные материалы Вы можете скачать здесь.
Введение
В настоящее время алгоритмы машинного обучения находят широкое применение в системах различного назначения: поисковых системах, алгоритмах распознавания, анализа и синтеза речи, медицинской диагностике, биоинформатике, финансовом прогнозировании и т.д. Исключением не является и компьютерное зрение. Например, подавляющее большинство современных систем детектирования объектов на изображениях и видео основано на применении алгоритмов машинного обучения. Такой подход позволяет компьютерной системе самой "научиться" отличать изображения, содержащие искомый объект, от остальных, используя для этого лишь примеры таких изображений. Также кластеризация и обучение с учителем успешно применяется в алгоритмах классификации изображений, опять же позволяя автоматически установить неявные различия между изображениями различных типов.
В настоящей работе рассматриваются некоторые алгоритмы обучения с учителем и кластеризации, реализованные в открытой библиотеке компьютерного зрения OpenCV [ 6 ].
1. Методические указания
1.1. Цели и задачи работы
Цель данной работы – изучить некоторые алгоритмы обучения с учителем и без с использованием соответствующих функций библиотеки компьютерного зрения OpenCV.
Данная цель предполагает решение следующих задач:
- Изучить основные идеи, лежащие в основе следующих алгоритмов классификации:
- машина опорных векторов;
- дерево решений;
- случайный лес;
- градиентный бустинг деревьев решений.
- Изучить идеи метода центров тяжести (k-means) для кластеризации.
- Рассмотреть прототипы функций и интерфейсы классов, реализующих перечисленные алгоритмы в библиотеке OpenCV.
- Рассмотреть простые примеры использования указанного набора функций.
- Разработать приложения для решения задач классификации и кластеризации рассмотренными методами.
- Применить разработанное приложение для решения модельных задач и проанализировать полученные результаты.
1.2. Структура работы
В работе приводится краткое описание некоторых алгоритмов классификации и кластеризации. Приводятся и описываются интерфейсы структур и классов, прототипы функций библиотеки OpenCV, реализующих рассматриваемые алгоритмы. Предлагаются примеры программ, демонстрирующие использование данных классов и функций. Приводятся результаты работы алгоритмов на модельных задачах. Разрабатывается структура приложений, для решения задач классификации и кластеризации.
1.3. Тестовая инфраструктура
Вычислительные эксперименты проводились с использованием следующей инфраструктуры (табл. 3.1).
| Операционная система | Microsoft Windows 7 |
| Среда разработки | Microsoft Visual Studio 2010 |
| Библиотека TBB | Intel® Threading Building Blocks 3.0 for Windows, Update 3 (в составе Intel® ParallelStudio XE 2011 SP1) |
| Библиотеки OpenCV | Версия 2.4.2 |
1.4. Требования к участнику лабораторной работы
Для выполнения данной лабораторной работы требуется:
- Изучение лекционного материала курса по теме "Обзор библиотек OpenCV и IPP"
- Изучение практического материала курса по теме "Сборка и установка библиотеки OpenCV. Использование библиотеки в среде разработки Microsoft Visual Studio"
- Изучение лекционного материала курса по теме "Введение в машинное обучение".
1.5. Рекомендации по проведению занятий
При выполнении данной лабораторной работы рекомендуется следующая последовательность действий:
- Привести примеры задач и приложений компьютерного зрения, которые могут решаться с помощью алгоритмов машинного обучения.
- Последовательно рассмотреть принципы, положенные в основу рассматриваемых методов. Параллельно описать классы и функции библиотеки OpenCV, реализующие данные алгоритмы, и продемонстрировать примеры программ, в которых выполняется их применение.
- Разработать структуру приложения, поддерживающего все рассмотренные алгоритмы обучения с учителем. Пояснить общую логику работы программы и описать функции, требующие реализации. Поставить задачу по исследованию качества решения модельных задач.
- Разработать структуру приложения, осуществляющего кластеризацию методом k-means. Пояснить общую логику работы программы и описать места, требующие реализации. Поставить задачу по исследованию качества решения модельных задач.
2. Обзор возможностей библиотеки OpenCV для решения задач обучения с учителем
2.1. Задача обучения с учителем
Одной из задач, изучаемой в машинном обучении, является задача обучения с учителем, которая заключается в как можно более точном восстановлении (определении) вида зависимости 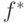 некоторой величины
некоторой величины  , от вектора
, от вектора 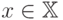 по конечному набору пар (прецедентов)
по конечному набору пар (прецедентов) 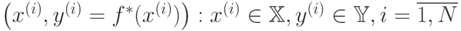 , называемому обучающей выборкой. Множество
, называемому обучающей выборкой. Множество  называется пространством признаков, компоненты вектора
называется пространством признаков, компоненты вектора 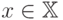 , в свою очередь, признаками,
, в свою очередь, признаками,  – целевым признаком или выходом. В рамках данной лабораторной работы будет рассматриваться конечное и неупорядоченное множество
– целевым признаком или выходом. В рамках данной лабораторной работы будет рассматриваться конечное и неупорядоченное множество 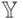 (далее будем предполагать, что
(далее будем предполагать, что 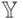 состоит из целых чисел, не используя никакие отношения порядка), т.е. решать задачу классификации. Также в качестве множества
состоит из целых чисел, не используя никакие отношения порядка), т.е. решать задачу классификации. Также в качестве множества  будем рассматривать d-мерное вещественное пространство
будем рассматривать d-мерное вещественное пространство 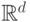 .
.
Алгоритмы, решающие задачу обучения с учителем, выполняют поиск функции (модели)  из некоторого фиксированного множества
из некоторого фиксированного множества 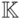 , зависящего от конкретного алгоритма. Процесс выбора функции
, зависящего от конкретного алгоритма. Процесс выбора функции  называется обучением.
называется обучением.
Для оценки качества построенной модели зависимости  от
от  используется множество прецедентов, не использовавшихся на этапе обучения, на котором вычисляется некоторый функционал качества (для задачи классификации, зачастую, рассматривается доля неверно классифицированных прецедентов).
используется множество прецедентов, не использовавшихся на этапе обучения, на котором вычисляется некоторый функционал качества (для задачи классификации, зачастую, рассматривается доля неверно классифицированных прецедентов).
Модуль ML библиотеки OpenCV содержит реализации следующих алгоритмов обучения с учителем: нормальный байесов классификатор, метод k ближайших соседей, нейронная сеть, машина опорных векторов, дерево решений, различные алгоритмы бустинга деревьев решений, в том числе градиентный бустинг, случайный лес и крайне случайный лес [ 1 ]. Каждый алгоритм обладает своими достоинствами и недостатками. Различные алгоритмы имеют свои ограничения применимости, например, могут быть предназначены только для задач классификации/восстановления регрессии, могут допускать работу лишь с количественными признаками, могут не поддерживать наличие пропущенных значений, т.е. неизвестных значений некоторых признаков у какого-либо прецедента. Также, тип функции, получаемой на выходе определенного алгоритма обучения, может лучше/хуже подходить для аппроксимации искомой зависимости. Таким образом, конкретный алгоритм обучения с учителем должен выбираться, исходя из специфики конкретной рассматриваемой задачи. Данная лабораторная работа посвящена описанию использования реализаций следующих алгоритмов: машина опорных векторов, дерево решений, случайный лес и градиентный бустинг деревьев решений.

