|
При прохождении теста 1 в нем оказались вопросы, который во-первых в 1 лекции не рассматривались, во-вторых, оказалось, что вопрос был рассмаотрен в самостоятельно работе №2. Это значит, что их нужно выполнить перед прохождением теста? или это ошибка? |
Машинное обучение
4.2. Разработка приложения для решения задач кластеризации
4.2.1. Требования к приложению
Также в рамках данной лабораторной работы предлагается разработать приложение для кластеризации точек методом центров тяжести. К приложению предъявляются следующие требования:
- Загрузка данных из файла, имя которого указывается в качестве параметра командной строки.
- Выполнение кластеризации на заданное (в виде аргумента командной строки) число кластеров.
- Визуализация кластеризации в двумерном пространстве.
4.2.2. Структура приложения
Приложение будет состоять из двух модулей: основной (main.cpp) и модуль визуализации (drawingFunctions.cpp/h). Функции визуализации предоставляются в готовом виде и аналогичны описанным в разделе 4.1.2.
В основном модуле должна выполняться следующая последовательность действий:
- Загрузка данных для кластеризации из файла.
- Выполнение кластеризации методом центров тяжести на указанное количество кластеров.
- Визуализация результата.
Код, необходимый для загрузки и визуализации предоставляется в готовом виде, следовательно, требуется лишь написать вызов функции кластеризации kmeans.
После того, как код основного модуля будет дописан, предлагается запустить программу на предоставленных наборах данных (dataset1.yml, dataset2.yml, dataset3.yml, dataset4.yml) и проанализировать полученные результаты.
5. Контрольные вопросы
- Для чего в алгоритме опорных векторов применяются ядра?
- Какой эффект можно наблюдать при использовании машины опорных векторов с радиальным ядром с большим значением параметра
 ?
? - Каким образом дерево решений разбивает пространство признаков?
- Для чего к деревьям решений применяется процедура отсечений?
- Применяются ли отсечения к деревьям решений в составе случайного леса?
- Происходит ли переобучение при увеличении количества деревьев в случайном лесе?
- Происходит ли переобучение при увеличении количества деревьев в модели градиентного бустинга?
- В чем заключается идея метода центров тяжести?
6. Дополнительные задания
- Реализуйте возможность сохранения и загрузки обученной модели в приложении для решения задач классификации.
- Реализуйте функцию вычисления матрицы ошибок классификации
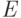 , где элемент
, где элемент 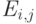 равен количеству прецедентов выборки принадлежащих к классу
равен количеству прецедентов выборки принадлежащих к классу  и отнесенных алгоритмом классификации к классу
и отнесенных алгоритмом классификации к классу  .
. - Реализуйте метод перекрестного контроля для подбора параметров алгоритмов обучения.

