|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Проектирование реляционных баз данных на основе принципов нормализации: первые шаги нормализации
Перекрывающиеся возможные ключи и нормальная форма Бойса-Кодда
До сих пор в определениях нормальных форм мы предполагали, что у декомпозируемого отношения имеется только один возможный ключ. На практике чаще всего бывает именно так. Но имеется один частный случай, который (почти) удовлетворяет требованиям 2NF и 3NF, но, тем не менее, порождает аномалии обновления. Это тот случай, когда у отношения имеется несколько возможных ключей, и некоторые из этих возможных ключей "перекрываются", т. е. содержат общие атрибуты.
Аномалии обновлений, связанные с наличием перекрывающихся возможных ключей
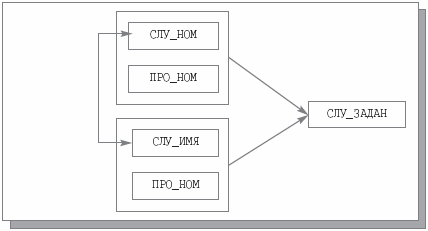
Например, пусть имеется переменная отношения СЛУЖ_ПРО_ЗАДАН1 {СЛУ_НОМ, СЛУ_ИМЯ, ПРО_НОМ, СЛУ_ЗАДАН} с множеством FD, показанным на рис. 7.7.
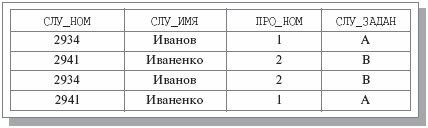
В отношении СЛУЖ_ПРО_ЗАДАН1 служащие уникально идентифицируются как по номерам удостоверений, так и по именам. Следовательно, существуют FD СЛУ_НОМ->СЛУ_ИМЯ и СЛУ_ИМЯ->СЛУ_НОМ. Но один служащий может участвовать в нескольких проектах, поэтому возможными ключами являются {СЛУ_НОМ, ПРО_НОМ} и {СЛУ_ИМЯ, ПРО_НОМ}. На рис. 7.8 показано возможное значение переменной отношения СЛУЖ_ПРО_ЗАДАН1.
Очевидно, что, хотя в отношении СЛУЖ_ПРО_ЗАДАН1 все FD неключевых атрибутов от возможных ключей являются минимальными и транзитивные FD отсутствуют, этому отношению свойственны аномалии обновления. Например, в случае изменения имени служащего требуется обновить атрибут СЛУ_ИМЯ во всех кортежах отношения СЛУЖ_ПРО_ЗАДАН1, соответствующих данному служащему. Иначе будет нарушена FD СЛУ_НОМ->СЛУ_ИМЯ, и база данных окажется в несогласованном состоянии.
Нормальная форма Бойса-Кодда
Причиной отмеченных аномалий является то, что в требованиях 2NF и 3NF не требовалась минимальная функциональная зависимость от первичного ключа атрибутов, являющихся компонентами других возможных ключей. Проблему решает нормальная форма, которую исторически принято называть нормальной формой Бойса-Кодда и которая является уточнением 3NF в случае наличия нескольких перекрывающихся возможных ключей.
Переменная отношения находится в нормальной форме Бойса-Кодда (BCNF) в том и только в том случае, когда любая выполняемая для этой переменной отношения нетривиальная и минимальная FD имеет в качестве детерминанта некоторый возможный ключ данного отношения.
Переменная отношения СЛУЖ_ПРО_ЗАДАН1 может быть приведена к BCNF путем одной из двух декомпозиций: СЛУЖ_НОМ_ИМЯ {СЛУ_НОМ, СЛУ_ИМЯ} и СЛУЖ_НОМ_ПРО_ЗАДАН {СЛУ_НОМ, ПРО_НОМ, СЛУ_ЗАДАН} с множеством FD и значениями, показанными на рис. 7.9, и СЛУЖ_НОМ_ИМЯ {СЛУ_НОМ, СЛУ_ИМЯ} и СЛУЖ_ИМЯ_ПРО_ЗАДАН {СЛУ_ИМЯ, ПРО_НОМ, СЛУ_ЗАДАН} (FD и значения результирующих переменных отношений выглядят аналогично).
Очевидно, что каждая из декомпозиций устраняет трудности, связанные с обновлением отношения СЛУЖ_ПРО_ЗАДАН1.
Всегда ли следует стремиться к BCNF?
Предположим теперь, что в организации все проекты включают разные задания, и по-прежнему каждый служащий может участвовать в нескольких проектах, но может выполнять в каждом проекте только одно задание. Одно задание в каждом проекте могут выполнять несколько служащих. Тогда переменная отношения СЛУЖ_ПРО_ЗАДАН имеет множество FD, показанное на рис. 7.10, и может содержать значение, представленное на том же рисунке.
В этом отношении существуют два возможных ключа: {СЛУ_НОМ, ПРО_НОМ} и {СЛУ_НОМ, СЛУ_ЗАДАН}. Отношение удовлетворяет требованиям 3NF: отсутствуют неминимальные FD неключевых атрибутов от возможных ключей (поскольку нет неключевых атрибутов) и отсутствуют транзитивные FD. Однако из-за наличия FD СЛУ_ЗАДАН->ПРО_НОМ это отношение не находится в BCNF. Поэтому отношению СЛУ_ПРО_ЗАДАН снова свойственны аномалии обновления. Например (поскольку СЛУ_НОМ является компонентом обоих возможных ключей), невозможно удалить данные о единственном служащем, выполняющем задание в некотором проекте, не утратив информацию об этом задании.
Можно привести отношение СЛУЖ_ПРО_ЗАДАН к BCNF, выполнив его декомпозицию на отношения СЛУЖ_НОМ_ЗАДАН {СЛУ_НОМ, СЛУ_ЗАДАН}8Единственным возможным ключом отношения СЛУЖ_НОМ_ЗАДАН является {СЛУ_НОМ, СЛУ_ЗАДАН}, и в этом отношении отсутствуют нетривиальные FD. и ПРО_НОМ_ЗАДАН {СЛУ_ЗАДАН, ПРО_НОМ}, и эта декомпозиция решает обозначенные проблемы (теперь можно хранить данные о задании проекта, не выполняемом ни одним служащим). Значения переменных отношений СЛУЖ_НОМ_ЗАДАН и ПРО_НОМ_ЗАДАН показаны на рис. 7.11.
Однако возникают новые трудности. Например, система должна запретить добавление в отношение СЛУЖ_НОМ_ЗАДАН кортежа <2934, D>, поскольку задание D относится к проекту 1, а служащий с номером 2934 уже выполняет задание в этом проекте. Так происходит, потому что исходная FD {СЛУ_НОМ, ПРО_НОМ}->СЛУ_ЗАДАН не выводится из единственной (нетривиальной) действующей для этих проекций FD СЛУ_ЗАДАН->ПРО_НОМ, и соответствующее ограничение целостности становится ограничением базы данных.
Тем самым, проекции СЛУЖ_НОМ_ЗАДАН и ПРО_НОМ_ЗАДАН не являются независимыми, а отношение СЛУЖ_ПРО_ЗАДАН атомарно, хотя и не находится в BCNF. Из этого следует, что при проектировании реляционной базы данных приведение отношения к BCNF не должно быть самоцелью. Нужно внимательно оценивать положительные и отрицательные последствия нормализации.
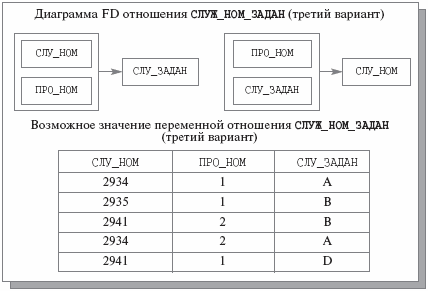
Наконец, приведем пример, когда наличие двух перекрывающихся возможных ключей не мешает отношению находиться в BCNF. Предположим, что в организации проекты включают одни и те же задания, каждый служащий может участвовать в нескольких проектах, но может выполнять в каждом проекте только одно задание. Тогда переменная отношения СЛУЖ_НОМ_ЗАДАН имеет множество FD, показанное на рис. 7.12, и может содержать значение, показанное на том же рисунке.
В третьем варианте отношения СЛУЖ_НОМ_ЗАДАН имеются перекрывающиеся возможные ключи ( {СЛУ_НОМ, ПРО_НОМ} и {ПРО_НОМ, СЛУ_ЗАДАН} ), однако оно находится в BCNF, поскольку эти ключи являются единственными детерминантами. Легко убедиться, что отношению СЛУЖ_НОМ_ЗАДАН аномалии обновления не свойственны.
Заключение
В этой лекции мы обсудили три начальные нормальные формы отношений – вторую и третью нормальные формы и нормальную форму Бойса-Кодда, – которые производятся путем декомпозиции без потерь исходного отношения на две проекции, где отсутствуют аномалии изменений, существовавшие в исходном отношении по причине наличия функциональных зависимостей с нежелательными свойствами.
Нормализация схемы базы данных способствует более эффективному выполнению системой управления базами данных операций обновления базы данных, поскольку сокращается число проверок и вспомогательных действий, поддерживающих целостность базы данных. При проектировании реляционной базы данных почти всегда добиваются второй нормальной формы всех входящих в базу данных отношений. В часто обновляемых базах данных обычно стараются обеспечить третью нормальную форму отношений. На нормальную форму Бойса-Кодда внимание обращают гораздо реже, поскольку на практике ситуации, в которых у отношения имеется несколько составных перекрывающихся возможных ключей, встречаются нечасто.