|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Базисные средства манипулирования реляционными данными: реляционная алгебра Кодда
Введение
Как мы отмечали в предыдущей лекции, в манипуляционной составляющей реляционной модели данных определяются два базовых механизма манипулирования реляционными данными – основанная на теории множеств реляционная алгебра и базирующееся на математической логике (точнее, на исчислении предикатов первого порядка) реляционное исчисление. В свою очередь, обычно выделяются два вида реляционного исчисления – исчисление кортежей и исчисление доменов.
Все эти механизмы обладают одним важным свойством: они замкнуты относительно понятия отношения. Это означает, что выражения реляционной алгебры и формулы реляционного исчисления определяются над отношениями реляционных БД и результатом их "вычисления" также являются отношения (конечно, здесь имеются в виду значения-отношения). В результате любое выражение или формула могут интерпретироваться как отношения, что позволяет использовать их в других выражениях или формулах.
Как мы увидим, алгебра и исчисление обладают большой выразительной мощностью: очень сложные запросы к базе данных могут быть выражены с помощью одного выражения реляционной алгебры или одной формулы реляционного исчисления. Именно по этой причине такие механизмы включены в реляционную модель данных. Конкретный язык манипулирования реляционными БД называется реляционно-полным, если любой запрос, формулируемый с помощью одного выражения реляционной алгебры или одной формулы реляционного исчисления, может быть сформулирован с помощью одного оператора этого языка.
Известно (и мы не будем это доказывать), что механизмы реляционной алгебры и реляционного исчисления эквивалентны, т. е. для любого допустимого выражения реляционной алгебры можно построить эквивалентную (т. е. производящую такой же результат) формулу реляционного исчисления и наоборот. Почему же в реляционной модели данных присутствуют оба эти механизма?
Дело в том, что они различаются уровнем процедурности. Выражения реляционной алгебры строятся на основе алгебраических операций (высокого уровня), и подобно тому, как интерпретируются арифметические и логические выражения, выражение реляционной алгебры также имеет процедурную интерпретацию. Другими словами, запрос, представленный на языке реляционной алгебры, может быть вычислен на основе выполнения элементарных алгебраических операций с учетом их приоритетности и возможного наличия скобок. Для формулы реляционного исчисления однозначная вычислительная интерпретация, вообще говоря, отсутствует. Формула только ставит условия, которым должны удовлетворять кортежи результирующего отношения. Поэтому языки реляционного исчисления являются в большей степени непроцедурными, или декларативными.
Поскольку механизмы реляционной алгебры и реляционного исчисления эквивалентны, в конкретной ситуации для проверки степени реляционности некоторого языка БД можно пользоваться любым из этих механизмов.
Заметим, что крайне редко алгебра или исчисление принимается в качестве полной основы какого-либо языка БД. Обычно (например, в случае языка SQL) язык основывается на некоторой смеси алгебраических и логических конструкций. Тем не менее знание алгебраических и логических основ языков баз данных часто применяется на практике.
Для экономии времени и места мы не будем вводить какие-либо строгие синтаксические конструкции, а в основном ограничимся рассмотрением материала на содержательном уровне.
Обзор реляционной алгебры Кодда
Основная идея реляционной алгебры состоит в том, что коль скоро отношения являются множествами, средства манипулирования отношениями могут базироваться на традиционных теоретико-множественных операциях, дополненных некоторыми специальными операциями, специфичными для реляционных баз данных.
Существует много подходов к определению реляционной алгебры, которые различаются наборами операций и способами их интерпретации, но, в принципе, являются более или менее равносильными. В данном разделе мы опишем немного расширенный начальный вариант алгебры, который был предложен Коддом (будем называть ее " алгеброй Кодда "). В этом варианте набор основных алгебраических операций состоит из восьми операций, которые делятся на два класса – теоретико-множественные операции и специальные реляционные операции. В состав теоретико-множественных операций входят операции:
- объединения отношений ;
- пересечения отношений ;
- взятия разности отношений ;
- взятия декартова произведения отношений.
Специальные реляционные операции включают:
Кроме того, в состав алгебры включается операция присваивания, позволяющая сохранить в базе данных результаты вычисления алгебраических выражений, и операция переименования атрибутов, дающая возможность корректно сформировать заголовок (схему) результирующего отношения.
Общая интерпретация реляционных операций
Если не вдаваться в некоторые тонкости, которые мы рассмотрим в следующих разделах, то почти для всех операций предложенного выше набора имеется очевидная и простая интерпретация.
- При выполнении операции объединения ( UNION ) двух отношений с одинаковыми заголовками производится отношение, включающее все кортежи, которые входят хотя бы в одно из отношений-операндов.
- Операция пересечения ( INTERSECT ) двух отношений с одинаковыми заголовками производит отношение, включающее все кортежи, которые входят в оба отношения-операнда.
- Отношение, являющееся разностью ( MINUS ) двух отношений с одинаковыми заголовками, включает все кортежи, входящие в отношение-первый операнд, такие, что ни один из них не входит в отношение, которое является вторым операндом.
- При выполнении декартова произведения ( TIMES ) двух отношений, пересечение заголовков которых пусто, производится отношение, кортежи которого производятся путем объединения кортежей первого и второго операндов.
- Результатом ограничения ( WHERE ) отношения по некоторому условию является отношение, включающее кортежи отношения-операнда, удовлетворяющее этому условию.
- При выполнении проекции ( PROJECT ) отношения на заданное подмножество множества его атрибутов производится отношение, кортежи которого являются соответствующими подмножествами кортежей отношения-операнда.
- При соединении ( JOIN ) двух отношений по некоторому условию образуется результирующее отношение, кортежи которого производятся путем объединения кортежей первого и второго отношений и удовлетворяют этому условию.
- У операции реляционного деления ( DIVIDE BY ) два операнда – бинарное и унарное отношения. Результирующее отношение состоит из унарных кортежей, включающих значения первого атрибута кортежей первого операнда таких, что множество значений второго атрибута (при фиксированном значении первого атрибута) включает множество значений второго операнда.
- Операция переименования ( RENAME ) производит отношение, тело которого совпадает с телом операнда, но имена атрибутов изменены.
- Операция присваивания ( := ) позволяет сохранить результат вычисления реляционного выражения в существующем отношении БД.
Поскольку результатом любой реляционной операции (кроме операции присваивания, которая не вырабатывает значения) является некое отношение, можно образовывать реляционные выражения, в которых вместо отношения-операнда некоторой реляционной операции находится вложенное реляционное выражение. В построении реляционного выражения могут участвовать все реляционные операции, кроме операции присваивания. Вычислительная интерпретация реляционного выражения диктуется установленными приоритетами операций:
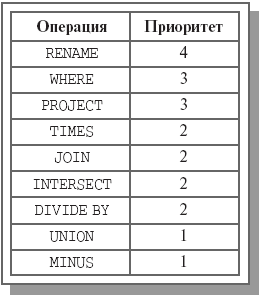
RENAME >= WHERE = PROJECT >= TIMES = JOIN = INTERSECT = DIVIDE BY >= UNION = MINUS
В другой форме приоритеты операций показаны на рис. 3.1. Вычисление выражения производится слева направо с учетом приоритетов операций и скобок.
Замкнутость реляционной алгебры и операция переименования
Как мы отмечали в предыдущей лекции, каждое значение-отношение характеризуется заголовком (или схемой) и телом (или множеством кортежей). Поэтому, если нам действительно нужна алгебра, операции которой замкнуты относительно понятия отношения, то каждая операция должна производить отношение в полном смысле, т. е. оно должно обладать и телом, и заголовком. Только в этом случае можно будет строить вложенные выражения.
Заголовок отношения представляет собой множество пар <имя-атрибута, имя-домена>. Если посмотреть на общий обзор реляционных операций, приведенный в предыдущем подразделе, то видно, что домены атрибутов результирующего отношения однозначно определяются доменами отношений-операндов. Однако с именами атрибутов результата не всегда все так просто.
Например, представим себе, что у отношений-операндов операции декартова произведения имеются одноименные атрибуты с одинаковыми доменами. Каким был бы заголовок результирующего отношения? Поскольку это множество, в нем не должны содержаться одинаковые элементы. Но и потерять атрибут в результате недопустимо. А это значит, что в таком случае вообще невозможно корректно выполнить операцию декартова произведения.
Аналогичные проблемы могут возникать и в случаях других двуместных операций. Для разрешения проблем в число операций реляционной алгебры вводится операция переименования. Ее следует применять в том случае, когда возникает конфликт именования атрибутов в отношениях-операндах одной реляционной операции. Тогда к одному из операндов сначала применяется операция переименования, а затем основная операция выполняется уже без всяких проблем. Более строго мы определим операцию переименования в следующей лекции, а пока лишь заметим, что результатом этой операции является отношение, совпадающее во всем с отношением-операндом, кроме того, что имя указанного атрибута изменено на заданное имя.
В дальнейшем изложении мы будем предполагать применение операции переименования во всех конфликтных ситуациях.