|
Хотелось бы иметь возможность читать текст сносок при использовании режима "Версия для печати" |
Базисные средства манипулирования реляционными данными: алгебра A Дейта и Дарвена
Операция реляционного дополнения
Пусть s обозначает результат операции <NOT> r. Тогда:
- Hs = Hr (заголовок результата совпадает с заголовком операнда);
-
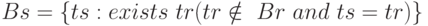 (в тело результата входят все кортежи, соответствующие заголовку и не входящие в тело операнда).
(в тело результата входят все кортежи, соответствующие заголовку и не входящие в тело операнда).
Операция <NOT> производит дополнение s заданного отношения r. Заголовком s является заголовок r. Тело s включает все кортежи, соответствующие этому заголовку и не входящие в тело r.
Видимо, следует пояснить, почему реляционный аналог операции логического отрицания называется здесь операцией реляционного дополнения. Во-первых, термин "дополнение" полностью соответствует сути операции <NOT>: тело результата операции <NOT> r является дополнением Br до полного множества кортежей, соответствующих Hr. Во-вторых, это не противоречит природе булевской операции NOT: у булевского типа имеются всего два значения – true и false, и NOT true = false, а NOT false = true. (Кстати, обратите внимание, что операцию NOT в трехзначной логике (см. лекцию 1) уже нельзя считать операцией дополнения.)
Чтобы привести пример использования операции <NOT>, предположим, что в состав домена ДОПУСТИМЫЕ_НОМЕРА_ПРОЕКТОВ, на котором определен атрибут ПРО_НОМ отношения НОМЕРА_ПРОЕКТОВ с рис. 4.1 слева, входит всего пять значений {1, 2, 3, 4, 5}. Тогда результат операции <NOT> НОМЕРА_ПРОЕКТОВ будет таким, как показано на рис. 4.1 справа.
Операция удаления атрибута
Пусть s обозначает результат операции r <REMOVE> A. Для обеспечения возможности выполнения операции требуется, чтобы существовал некоторый тип (или домен) T такой, что  (т. е. в состав заголовка отношения r должен входить атрибут A ). Тогда:
(т. е. в состав заголовка отношения r должен входить атрибут A ). Тогда:
- Hs = Hr minus {<A, T>}, т. е. заголовок результата получается из заголовка операнда изъятием атрибута A ;
-
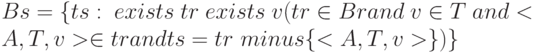 , т. е. в тело результата входят все кортежи операнда, из которых удалено значение атрибута A.
, т. е. в тело результата входят все кортежи операнда, из которых удалено значение атрибута A.
Операция <REMOVE> производит отношение s, формируемое путем удаления указанного атрибута A из заданного отношения r. Операция эквивалентна взятию проекции r на все атрибуты, кроме A. Заголовок s получается теоретико-множественным вычитанием из заголовка r множества из одного элемента {<A, T>}. Тело s состоит из таких кортежей, которые соответствуют заголовку s, причем каждый из них является подмножеством некоторого кортежа тела отношения r.
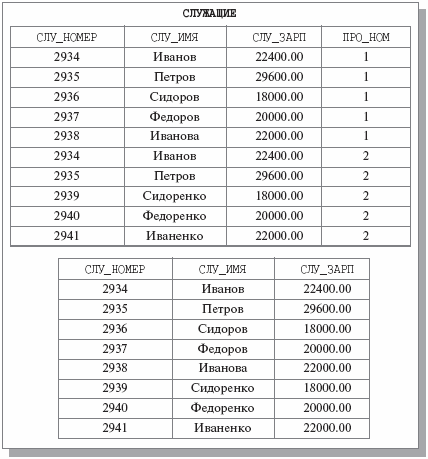
Примером операции REMOVE (конечно же, очень похожим на пример использования операции PROJECT из предыдущей лекции) является СЛУЖАЩИЕ REMOVE ПРО_НОМ (получить данные о служащих, участвующих в проектах). Результат этой операции над отношением СЛУЖАЩИЕ, тело которого приведено в верхней части рис. 4.2, показан на рис. 4.2 внизу.
Операция переименования
Пусть s обозначает результат операции r <RENAME> (A, B). Для обеспечения возможности выполнения операции требуется, чтобы существовал некоторый тип T, такой, что  , и чтобы не существовал такой тип T, что
, и чтобы не существовал такой тип T, что 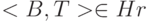 . (Другими словами, в схеме отношения r должен присутствовать атрибут A и не должен присутствовать атрибут B.) Тогда:
. (Другими словами, в схеме отношения r должен присутствовать атрибут A и не должен присутствовать атрибут B.) Тогда:
- Hs = (Hr minus {<A, T>}) union {<B, T>}, т. е. в схеме результата B заменяет A ;
-
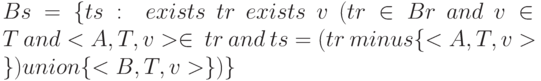 , т. е. в кортежах тела результата имя значений атрибута A меняется на B.
, т. е. в кортежах тела результата имя значений атрибута A меняется на B.
Операция <RENAME> производит отношение s, которое отличается от заданного отношения r только именем одного его атрибута, которое изменяется с A на B. Заголовок s такой же, как заголовок r, за исключением того, что пара <B, T> заменяет пару <A, T>. Тело s включает все кортежи тела r, но в каждом из этих кортежей триплет <B, T, v> заменяет триплет <A, T, v>.
По причине очевидности пример использования этой операции мы приводить не будем.