|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Экономико-математические модели и принятие решений
Примеры типовых макроэкономических моделей
Модель межотраслевого баланса (модель В. Леонтьева). Каждая из n отраслей производит свой (обобщенный) продукт. Выпуск распределяется в заданной пропорции между конечным потреблением, другими отраслями и внутренними потребностями отрасли. Кроме того, описывается прирост производственных мощностей. Модель описывается уравнениями:
![\upsilon_j(t)=\sum_{j=1}^n \left[a_{ij} \upsilon_j(t)+b_{ij}\frac{dV_j(t+ \tau_i)}{dt}\right]+P_j(t), i=1,2,\dots, n](/sites/default/files/tex_cache/716f4a02070c7664b230accfc5be8ac4.png)
где 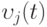 - поток выпуска продукта
- поток выпуска продукта  в момент времени
в момент времени  (единица измерения = единица продукта / единица времени);
(единица измерения = единица продукта / единица времени);
 - мощность
- мощность  - го производства или максимальный выпуск;
- го производства или максимальный выпуск;
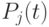 - поток конечного (непроизводственного) потребления;
- поток конечного (непроизводственного) потребления;
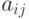 - коэффициенты прямых сырьевых затрат (количество продукта
- коэффициенты прямых сырьевых затрат (количество продукта  , необходимое для производства продукта
, необходимое для производства продукта  );
);
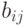 - количество фондообразующего продукта
- количество фондообразующего продукта 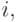 идущее на единичный прирост мощности в отрасли
идущее на единичный прирост мощности в отрасли  ;
;
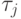 - продолжительность строительства мощности в отрасли
- продолжительность строительства мощности в отрасли 
Таким образом, выпуск 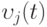 расходуется на покрытие сырьевых и фондообразующих затрат и конечное потребление.
расходуется на покрытие сырьевых и фондообразующих затрат и конечное потребление.
Эконометрические модели народного хозяйства (типа Брукингской и Уортоновской). В основе этих моделей лежат: 1) балансовые соотношения; 2) функциональные зависимости - производственная функция и функция потребительского спроса.
Производственная функция 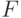 задает зависимость национального дохода
задает зависимость национального дохода 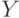 от стоимости основных фондов (капитала)
от стоимости основных фондов (капитала) 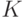 и от используемых трудовых ресурсов
и от используемых трудовых ресурсов 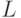 :
:
![Y(t)=F[K(t), L(t)]](/sites/default/files/tex_cache/73aa623e073819a338242f53e3934d95.png)
Функция спроса  задает зависимость вектора
задает зависимость вектора 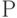 конечного потребления, т.е. набора потребляемых товаров, от вектора с цен на эти товары и дохода
конечного потребления, т.е. набора потребляемых товаров, от вектора с цен на эти товары и дохода 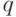 .
.
Паутинообразные модели имеют дело с динамикой спроса и предложения. Пусть 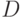 - спрос,
- спрос, 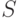 - предложение,
- предложение, 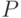 - цена,
- цена, 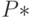 - равновесная цена,
- равновесная цена,  - объем производства,
- объем производства,  - равновесный объем производства. Равновесные
- равновесный объем производства. Равновесные 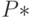 и
и  находят из условия совпадения спроса и предложения
находят из условия совпадения спроса и предложения 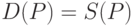 .
.
Однако более реалистичной является гипотеза запаздывания предложения. Например, пусть при цене в прошлый период 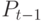 объем предложения в данный период есть
объем предложения в данный период есть  . Считаем, что цена
. Считаем, что цена  устанавливается на рынке так, чтобы был куплен весь объем выпущенной продукции
устанавливается на рынке так, чтобы был куплен весь объем выпущенной продукции 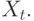 Следовательно,
Следовательно,

Пусть спрос и предложение достаточно точно описываются линейными функциями от цены
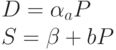
Такое предположение вполне естественно, если в модели рассматривается окрестность точки равновесия, а функции спроса и предложения гладкие. Тогда
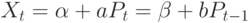 |
( 1) |
Равновесие наступает, когда
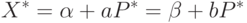 |
( 2) |
Вычитая (1) из (2), получаем, что
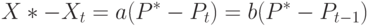 |
( 3) |
Обозначим  - отклонения от равновесия. Из (3) получим
- отклонения от равновесия. Из (3) получим 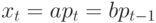 , откуда
, откуда 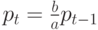 Решение этого уравнения имеет вид
Решение этого уравнения имеет вид 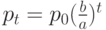
В зависимости от того, чему равно  , получим либо затухающие колебания
, получим либо затухающие колебания 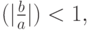 сходящиеся к
сходящиеся к 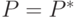 и
и 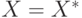 , либо колебания c возрастающей амплитудой
, либо колебания c возрастающей амплитудой  . В промежуточном случае
. В промежуточном случае 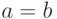 амплитуда колебаний постоянна.
амплитуда колебаний постоянна.
Тот же результат справедлив и в модели с непрерывным временем. Будем считать, что спрос меняется не только в зависимости от цены, но и в зависимости от ее динамики, т.е.
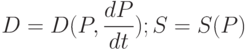
Тогда аналогом (13.1) является уравнение 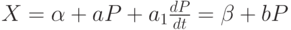 , решением которого является
, решением которого является 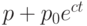
В рассматриваемых моделях считалось, что производители ожидают, что цена останется, как в предшествующий период (и устанавливают объем изготавливаемого товара исходя из этих ожиданий). Модель может быть усовершенствована. Для установления объема изготавливаемого товара производителям более реалистично считать, что в момент времени  цена на товар будет равна
цена на товар будет равна 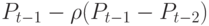 , где
, где  , т.е. цена изменится в направлении, обратном тому, в котором она изменялась в прошлый период. Тогда
, т.е. цена изменится в направлении, обратном тому, в котором она изменялась в прошлый период. Тогда 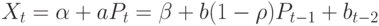 , следовательно,
, следовательно, 
Дальнейшее развитие модели состоит во введении в нее запасов. Ожидая повышения цен, продавцы создают запасы товара.
Запасы в момент времени  обозначим
обозначим 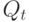 . Тогда изменение запасов за период времени от t-1 до t есть
. Тогда изменение запасов за период времени от t-1 до t есть 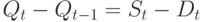 . В модели цену можно устанавливать различными способами, например,
. В модели цену можно устанавливать различными способами, например, 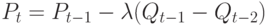 или
или 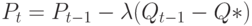 , где
, где 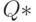 - запасы в точке равновесия. В первом случае получим
- запасы в точке равновесия. В первом случае получим 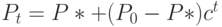 , где
, где 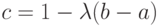 , а во втором -
, а во втором -  .
.
Модель экономического цикла. Сначала рассмотрим простую модель без учета запаздывания, а также без учета экспорта-импорта, налогов и государственных расходов.
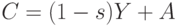 |
( 4) |
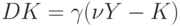 |
( 5) |
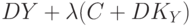 |
( 6) |
где 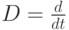 - символ операции дифференцирования;
- символ операции дифференцирования;  - реальный чистый доход,
- реальный чистый доход,  - реальное потребление,
- реальное потребление,  - объем основного капитала,
- объем основного капитала, 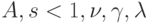 - положительные константы. Более точно,
- положительные константы. Более точно,  - сумма всех видов конечных доходов, полученных в народном хозяйстве, деленная на индекс инфляции (т.е. реальный валовой национальный продукт за вычетом затрат на возмещение основного капитала);
- сумма всех видов конечных доходов, полученных в народном хозяйстве, деленная на индекс инфляции (т.е. реальный валовой национальный продукт за вычетом затрат на возмещение основного капитала);  - общие затраты на потребительские товары конечных покупателей в народном хозяйстве, деленные на индекс инфляции; K - объем основного капитала всего народного хозяйства (в сопоставимых ценах).
- общие затраты на потребительские товары конечных покупателей в народном хозяйстве, деленные на индекс инфляции; K - объем основного капитала всего народного хозяйства (в сопоставимых ценах).
Уравнение (4) вытекает из теории Кейнса, а именно, из соотношения: потребление = национальный доход - сбережения + автономное потребление. Значит, 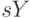 - часть дохода, идущая на сбережения,
- часть дохода, идущая на сбережения,  - предельная склонность к сбережениям,
- предельная склонность к сбережениям,  - автономное потребление (та доля потребления, которая не зависит от дохода, своеобразный прожиточный минимум).
- автономное потребление (та доля потребления, которая не зависит от дохода, своеобразный прожиточный минимум).
Уравнение (5) допускает несколько интерпретаций. Рассмотрим две из них.
1. В первой интерпретации 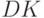 - это норма капитальных вложений в основной капитал. Допустим, существует оптимальный объем основного капитала и он равен некоторой доле от национального дохода -
- это норма капитальных вложений в основной капитал. Допустим, существует оптимальный объем основного капитала и он равен некоторой доле от национального дохода - 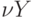 , где
, где  - оптимальное соотношение "капитал-выпуск". Тогда уравнение (5) означает, что норма капитальных вложений в основной капитал пропорциональна превышению оптимального объема основного капитала над действительным.
- оптимальное соотношение "капитал-выпуск". Тогда уравнение (5) означает, что норма капитальных вложений в основной капитал пропорциональна превышению оптимального объема основного капитала над действительным.
2. Основное соотношение, описывающее капитальные вложения, имеет вид:
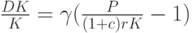 |
( 7) |
где P - реальная прибыль,  - норма процента,
- норма процента,  - премия за риск. Из соотношения (7) легко получить (5).
- премия за риск. Из соотношения (7) легко получить (5).
В уравнении (6)  - рост производства (поскольку все производство = всему доходу =
- рост производства (поскольку все производство = всему доходу =  ). Рост производства зависит от избытка спроса. Потребление (
). Рост производства зависит от избытка спроса. Потребление (  ) + накопление (оно превращается в капитальные вложения
) + накопление (оно превращается в капитальные вложения 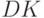 ) - чистый национальный доход (
) - чистый национальный доход (  ) - это и есть избыток спроса (то, что потребляется и накопляется, может быть не равно чистому доходу).
) - это и есть избыток спроса (то, что потребляется и накопляется, может быть не равно чистому доходу).
Для равновесной системы все производные по времени равны 0. Равновесные значения 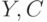 и
и  таковы:
таковы:
 |
( 8) |
 |
( 9) |
Этот результат не предназначен для непосредственного практического использования, т.к. в модели не учитываются ограничения на выпуск, накладываемые рабочей силой и объемом основного капитала. Однако он нужен, чтобы найти отклонения от равновесия 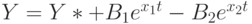 - решение системы (4)-(5)-(6)-(8)-(9), где
- решение системы (4)-(5)-(6)-(8)-(9), где  зависят от
зависят от 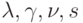 . В зависимости от
. В зависимости от  и
и  получим согласно теории линейных дифференциальных уравнений следующие четыре варианта траекторий
получим согласно теории линейных дифференциальных уравнений следующие четыре варианта траекторий  : 1) незатухающие колебания (экономические циклы); 2) затухающие колебания; 3) взрывоподобные колебания; 4) взрывоподобная, но не колебательная траектория.
: 1) незатухающие колебания (экономические циклы); 2) затухающие колебания; 3) взрывоподобные колебания; 4) взрывоподобная, но не колебательная траектория.
Довольно часто в экономике реально осуществляется приближение к первому варианту - экономические циклы.
Усложним модель, введем запаздывание. В модели (4)-(6) предполагается мгновенная реакция потребления на изменение дохода. На самом деле это неверно. Вместо уравнения (4) напишем
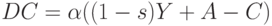 |
( 10) |
где  - параметр, определяющий быстродействие системы.
- параметр, определяющий быстродействие системы.
Теперь добавим запасы. Вместо уравнения (6) получим
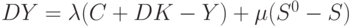 |
( 11) |
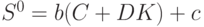 |
( 12) |
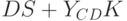 |
( 13) |
где  - оптимальный уровень запасов, равен некоторой постоянной величине + часть потребления и капитальных вложений,
- оптимальный уровень запасов, равен некоторой постоянной величине + часть потребления и капитальных вложений,  - фактический уровень запасов. Уравнение (11) отражает тот факт, что рост производства зависит от избытка спроса и от превышения оптимальных запасов над фактическими. (Уравнения (10) и (11) аналогичны соответствующим соотношениям для паутинообразных моделей.)
- фактический уровень запасов. Уравнение (11) отражает тот факт, что рост производства зависит от избытка спроса и от превышения оптимальных запасов над фактическими. (Уравнения (10) и (11) аналогичны соответствующим соотношениям для паутинообразных моделей.)
Добавим в систему экспорт-импорт, налоги и государственные расходы. Теперь с учетом (11)-(13) получим модель в виде системы уравнений
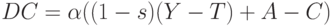 |
( 14) |
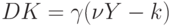 |
( 15) |
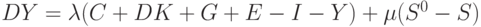 |
( 16) |
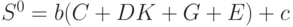 |
( 17) |
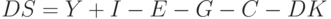 |
( 18) |
 |
( 19) |
 |
( 20) |
где  - реальный импорт,
- реальный импорт,  - реальный объем налогов за вычетом государственных трансфертных платежей,
- реальный объем налогов за вычетом государственных трансфертных платежей,  - реальный экспорт,
- реальный экспорт,  - реальные государственные расходы на товары и услуги.
- реальные государственные расходы на товары и услуги.
В уравнении (14) национальный доход, идущий на потребление и накопление, уменьшился на сумму налогов, т.е. по сравнению с (10) произошла замена 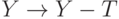 .
.
Далее заметим, что теперь  - общее потребление товаров как отечественного, так и импортного производства, а
- общее потребление товаров как отечественного, так и импортного производства, а 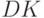 теперь есть рост основного капитала частного сектора. Накопление основного капитала частного сектора входит в
теперь есть рост основного капитала частного сектора. Накопление основного капитала частного сектора входит в  .
.
Уравнение (16) отличается от (11) на величину 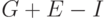 , т.к.
, т.к.  - рост производства зависит от избытка спроса, который теперь равен тому, что общество расходует (т.е. потребляет (
- рост производства зависит от избытка спроса, который теперь равен тому, что общество расходует (т.е. потребляет (  ) + вкладывает (
) + вкладывает ( 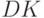 ) + экспорт (
) + экспорт (  ) + государственные расходы (
) + государственные расходы (  )) за вычетом того, что общество получает (национальный доход (
)) за вычетом того, что общество получает (национальный доход (  ) + импорт (
) + импорт (  )).
)).
Уравнение (17) предполагает, что желаемый уровень запасов есть линейная функция валового сбыта, а валовой сбыт это: 1) сбыт потребительских товаров отдельным потребителям  ; 2) сбыт капитальных благ фирмам (капитальные вложения)
; 2) сбыт капитальных благ фирмам (капитальные вложения) 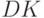 ; 3) сбыт товаров в государственном секторе
; 3) сбыт товаров в государственном секторе  ; 4) сбыт иностранным производителям
; 4) сбыт иностранным производителям  .
.
Уравнение (18) означает, что изменение запасов равно всем товарам  минус весь сбыт
минус весь сбыт 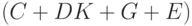 .
.
Уравнение (19) предполагает, что импорт - это доля всего сбыта.
Уравнение (20) предполагает, что налоги - линейная функция доходов, тогда 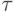 - аналог процентной ставки. То, что в уравнении имеется отрицательная константа
- аналог процентной ставки. То, что в уравнении имеется отрицательная константа  , говорит о том, что
, говорит о том, что  - возрастающая функция , т.е. чем больше доход, тем больше налог.
- возрастающая функция , т.е. чем больше доход, тем больше налог.
При решении системы (14)-(20) выяснилось, в частности, что введение налогов и импорта оказывает на экономику стабилизирующее воздействие.

