|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Дележ, отвечающий аксиомам Нэша
Из (15.10) и определения W выводим неравенство
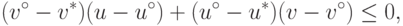
 |
( 15.16) |
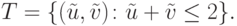 |
( 15.17) |
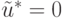 ,
, 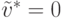 .
.Таким образом, линейное преобразование (15.15)
переводит задачу (W,u*,v*) в задачу (T,0,0),
удовлетворяющую условиям аксиомы симметрии.
Простота этой задачи позволяет найти отвечающую ей сделку, руководствуясь
непосредственно аксиомами Нэша. Требования рациональности, допустимости,
не улучшаемости и вытекающее из шестой аксиомы условие  удовлетворяются в единственной точке
удовлетворяются в единственной точке
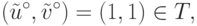 |
( 15.18) |
Отображая точку (15.18) на плоскость (u,v) в соответствии
с преобразованием (15.16) и принимая во внимание пятую аксиому, получаем, что пара  есть единственная отвечающая аксиомам сделка в
задаче (W,u*,v*). Наконец, учитывая включения
есть единственная отвечающая аксиомам сделка в
задаче (W,u*,v*). Наконец, учитывая включения  и четвертую аксиому, выводим,
что пара
и четвертую аксиому, выводим,
что пара  есть единственная удовлетворяющая
аксиомам сделка в исходной
задаче (S,u*,v*). Таким образом, единственная
удовлетворяющая аксиомам сделка совпадает с точкой
из определения (15.5).
есть единственная удовлетворяющая
аксиомам сделка в исходной
задаче (S,u*,v*). Таким образом, единственная
удовлетворяющая аксиомам сделка совпадает с точкой
из определения (15.5).
Завершение доказательства теоремы. Остается рассмотреть случаи, когда не выполняются предположения (15.2). При этом возможны следующие три ситуации:
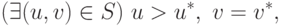 |
( 15.19) |
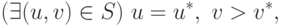 |
( 15.20) |
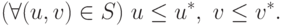 |
( 15.21) |
Рассмотрим случай (15.19) (случай (15.20)
рассматривается аналогично). Решение для таких задач
определяется оператором  вида
вида
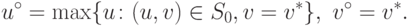 |
( 15.22) |
Решение (15.22) допустимо, рационально и неулучшаемо (для обеих сторон). Заметим также,
что оно является единственным решением, удовлетворяющим первым трем
аксиомам. Кроме того, правило (15.22)
определяет пару  как решение задачи
как решение задачи 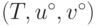 , если
, если  .
Т.е. четвертая аксиома также выполняется.
.
Т.е. четвертая аксиома также выполняется.
Любые преобразования вида (14.20)
переводят горизонтальный участок границы множества S,
лежащий на прямой u=v*, в горизонтальный участок границы
множества T, лежащий на прямой 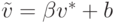 .
Следовательно, правило (15.22)
даст для задачи
.
Следовательно, правило (15.22)
даст для задачи 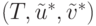 дележ
дележ 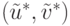 , согласующийся с пятой
аксиомой.
, согласующийся с пятой
аксиомой.
В случае (15.21), когда кооперация не может улучшить выигрыши сторон,
положим 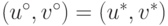 .
Соответствие такого решения аксиомам Нэша легко проверяемо.
.
Соответствие такого решения аксиомам Нэша легко проверяемо.
Вернемся к рассмотренным выше примерам. Дележ  ,
изображенный темным кружком в верхней части рис. 3.3, получен
с помощью графического построения. Построение выполнено в соответствии
с ранее описанным приемом. Этот дележ реализуется путем
согласованного использования обеими сторонами пары чистых
стратегий i=2, j=2 (см. табл. 3.1).
,
изображенный темным кружком в верхней части рис. 3.3, получен
с помощью графического построения. Построение выполнено в соответствии
с ранее описанным приемом. Этот дележ реализуется путем
согласованного использования обеими сторонами пары чистых
стратегий i=2, j=2 (см. табл. 3.1).
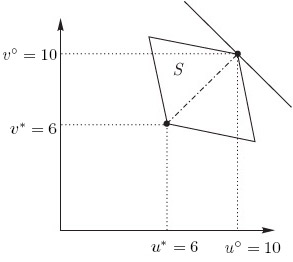
Допустимое множество  для рассмотренной в
"Нормальная форма конечной игры. Задание конечной игры в позиционной форме"
задачи об ограничениях при ловле рыбы, представлено на рис. 3.7.
Согласно (14.7)-(14.14), для содержащих седловые значения матриц этой задачи
справедливы оценки:
для рассмотренной в
"Нормальная форма конечной игры. Задание конечной игры в позиционной форме"
задачи об ограничениях при ловле рыбы, представлено на рис. 3.7.
Согласно (14.7)-(14.14), для содержащих седловые значения матриц этой задачи
справедливы оценки:
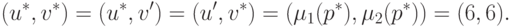
Решение 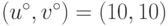 , оцененное графическим
способом (см. рис. 3.7), существенно превосходит выигрыши,
достижимые односторонними действиями участников. Таким образом, введение (по взаимному согласию
сторон) системы контроля за соблюдением соглашения (например, путем
организации проверок в местах лова рыбы) могло бы повысить их доходы (и
дать средства для содержания инспекторов).
, оцененное графическим
способом (см. рис. 3.7), существенно превосходит выигрыши,
достижимые односторонними действиями участников. Таким образом, введение (по взаимному согласию
сторон) системы контроля за соблюдением соглашения (например, путем
организации проверок в местах лова рыбы) могло бы повысить их доходы (и
дать средства для содержания инспекторов).
Допустимое множество для задачи о строительстве с долевым участием (см. "Стратегическое равновесие в 2 x 2 играх" ) уже рассматривал ось (см. рис. 3.2). Этому примеру соответствуют оценки
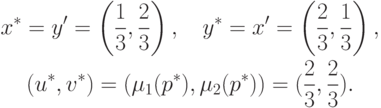
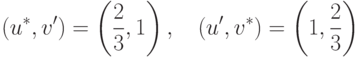
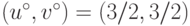 ,
реализуемой уже обсуждавшейся рулеткой (14.5).
,
реализуемой уже обсуждавшейся рулеткой (14.5).