|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Лекция 10: Приведение позиционной игры к игре в нормальной форме. Условия существования стратегического равновесия
Как уже отмечалось, игра в позиционной форме предусматривает принятие решений в каждой (реализующейся в ходе конкретной партии) позиции. Однако каждая сторона может заблаговременно составить свой план ведения игры, предусматривающий, какое решение должно быть выбрано на каждом ходе (если развитие игры приведет в позицию, соответствующую этому ходу). Принятие такого плана сводит многократные выборы решений в ходе игры к единственному выбору (т.е. к выбору плана, определяющего решения во всех позициях данной стороны). Будем называть эти планы стратегиями сторон в позиционной игре. Введенное понятие стратегии (плана ведения игры) допускает следующее формальное определение.
Определение 2.4 ( стратегии игрока в позиционной игре ). Стратегия стороны Pi, i=1,2,
в конечной позиционной игре  есть функция,
определенная на всех информационных множествах этой стороны
(в дереве игры
есть функция,
определенная на всех информационных множествах этой стороны
(в дереве игры  ). Значением этой функции на каждом таком
множестве является один из выборов, имеющихся у Pi в этом
множестве.
). Значением этой функции на каждом таком
множестве является один из выборов, имеющихся у Pi в этом
множестве.
В качестве иллюстрации определим стратегии сторон в описанном выше примере погони за конкурентом. Начнем со случая, когда сторона P2 заблаговременно информирована о первом выборе, осуществленном стороной P1. Дерево игры, соответствующее этому случаю (см. рис. 2.2), содержит два информационных множества (E1 и E2) стороны P1. Каждому из этих множеств соответствует один и тот же набор вариантов (МП2, МП5). Следовательно, возможны четыре стратегии стороны P1, представляемые следующими функциями:
 |
( 9.1) |
 |
( 9.2) |
 |
( 9.3) |
 |
( 9.4) |
Замечание 2.1 (о дублировании стратегий). Фактически, введенные выше стратегии s1 и s2 описывают одно и то же поведение стороны P1, ибо после выбора (в позиции q1 ) маршрута МП2 последующее развитие операции не может привести в позицию q4. Поэтому различие рекомендаций, касающихся выбора решения во множестве E2 (а именно этим и разнятся стратегии s1 и s2 ), не может влиять на развитие операции. Однако мы не будем стремиться исключить возникающую при этом избыточность описания, чтобы сохранить простое определение стратегии, введенное выше.
Аналогично можно перечислить все стратегии стороны P2, которой сопоставлены два информационных множества (C1 и C2), каждое из которых характеризуется одним и тем же набором вариантов решений (МП2, МП4); см. дерево игры на рис. 2.2. Множество этих стратегий составляют четыре функции:
 |
( 9.5) |
 |
( 9.6) |
 |
( 9.7) |
 |
( 9.8) |
Если принять, что информационные множества каждой стороны занумерованы, то можно характеризовать стратегии с помощью кортежей, число компонент которых соответствует числу информационных множеств (в дереве игры) для данного игрока. При этом кортеж составляется из вариантов, определяющих выбор в соответствующем множестве. Т.е. первый элемент кортежа соответствует выбору в первом информационном множестве, второй элемент - во втором множестве, и т.д. В соответствии с этим соглашением перечисленные выше стратегии сторон P1 и P2 можно записать в виде
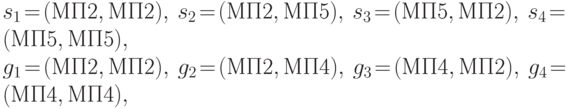
Пусть стороны P1 и P2 соответственно выбрали стратегии s и g. Прослеживая путь в дереве игры, определяемый теми выборами, которые предписывают стратегии s и g (в последовательно проходимых позициях), можно определить конкретный исход игры и уровни полезности, достигаемые сторонами в этом исходе. Тем самым определяются значения платежных функций M1(s,g) и M2(s,g). Например, в случае, когда P1 выбирает стратегию s4, а P2 - стратегию g3, игра заканчивается в исходе t5 и
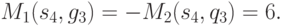
- выбор стороны P1 (в исходной позиции q1 ) есть МП5, и этот выбор переводит игру в позицию q3 ;
- выбор стороны P2 в позиции q3 есть МП2, и в результате следующей позицией становится q4 ;
- выбор P1 в позиции q4 есть МП5, что переводит игру в исход t5 (см. дерево игры на рис. 2.2).
Описанный способ определения значений для платежных функций сторон по заданным стратегиям и дереву игры позволяет привести позиционную игру к нормальной форме. Выполним такое приведение для рассмотренного примера. Начнем со случая, когда сторона P2 заблаговременно информирована о результатах первого выбора, осуществленного стороной P1. Соответствующие значения критерия M1(s,g) сведем в табл. 2.2.
| Матрица игры "погоня" (с полной информацией) | Стратегия P2 | ||||
| МП2, МП2 | МП2, МП4 | МП4, МП2 | МП4, МП4 | ||
| Стратегия P1 | МП2, МП2 | 2 | 2 | 4 | 4 |
| МП2, МП5 | 2 | 2 | 4 | 4 | |
| МП5, МП2 | 7 | 3 | 7 | 3 | |
| МП5, МП5 | 6 | 3 | 5 | 3 | |
Таблица такого вида уже рассматривалась как иллюстрация к определению седлового значения матрицы игры (см. "Нормальная форма конечной игры. Задание конечной игры в позиционной форме" ). При этом было установлено существование двух устойчивых и эффективных решений, определяемых парами стратегий (s3,g2) и (s4,g2). Цена этой антагонистической игры (т.е. седловое значение матрицы) равна 3.
В случае, когда сторона P2 в момент выбора своего маршрута не имеет информации о маршруте, реализуемом стороной P1, соответствующее дерево игры (см. рис. 2.5) содержит лишь одно информационное множество C={q2,q3} стороны P2. Следовательно, в этой частной задаче сторона P2 имеет лишь две стратегии:
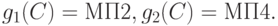
Матрица игры, соответствующая этому последнему случаю, представлена в табл. 2.3.
| Матрица игры "погоня" (при неполной информации) | Стратегия P2 | ||
| МП2 | МП4 | ||
| Стратегия P1 | МП2, МП2 | 2 | 4 |
| МП2, МП5 | 2 | 4 | |
| МП5, МП2 | 7 | 3 | |
| МП5, МП5 | 6 | 3 | |
Замечание 2.2 (о роли полной информации)
Полученная  матрица игры не содержит седловых значений (т.е.
в ней нет элементов, которые, будучи максимальными значениями в своих
столбцах, были бы одновременно и минимальными значениями в своих строках).
Следовательно, в рассмотренном примере не существует решений, обладающих
свойствами равновесия по Нэшу. При этом сторона P1, выбрав
стратегию s3 или s4, может (как и в случае полной
информированности) гарантированно уклоняться от одновременных и одноместных с P2
продаж своего товара в течение 3-х периодов времени. Однако другая сторона
(т.е. P2 ) уже не может гарантировать завершение погони через
3 периода времени. Время, необходимое ей для этого, составляет уже 4 периода. Таким
образом, устойчивое и эффективное решение, существовавшее в условиях,
когда каждая сторона выбирала свои решения, имея полную информацию обо
всех уже осуществленных выборах, исчезает, как только утрачивается полная
информированность сторон. Ниже будет показано, что полная
информированность является достаточным условием существования устойчивых
решений. Поэтому в тех случаях, когда обе стороны заинтересованы
в существовании устойчивых форм взаимодействия, они могут вводить механизмы
взаимных проверок, гарантирующие полную информированность.
матрица игры не содержит седловых значений (т.е.
в ней нет элементов, которые, будучи максимальными значениями в своих
столбцах, были бы одновременно и минимальными значениями в своих строках).
Следовательно, в рассмотренном примере не существует решений, обладающих
свойствами равновесия по Нэшу. При этом сторона P1, выбрав
стратегию s3 или s4, может (как и в случае полной
информированности) гарантированно уклоняться от одновременных и одноместных с P2
продаж своего товара в течение 3-х периодов времени. Однако другая сторона
(т.е. P2 ) уже не может гарантировать завершение погони через
3 периода времени. Время, необходимое ей для этого, составляет уже 4 периода. Таким
образом, устойчивое и эффективное решение, существовавшее в условиях,
когда каждая сторона выбирала свои решения, имея полную информацию обо
всех уже осуществленных выборах, исчезает, как только утрачивается полная
информированность сторон. Ниже будет показано, что полная
информированность является достаточным условием существования устойчивых
решений. Поэтому в тех случаях, когда обе стороны заинтересованы
в существовании устойчивых форм взаимодействия, они могут вводить механизмы
взаимных проверок, гарантирующие полную информированность.

