Проецирование пространственных сцен

Специальные картографические проекции. Экзотические проекции земной сферы

С развитием торговли и путешествий приобрела большую важность довольно непростая геометрическая задача: как перенести на плоскость часть земной поверхности, чтобы расстояния между любыми двумя точками на ней остались неискаженными? Различные ученые в течение многих веков пытались разрешить эту проблему по заказам своих правительств, крупных коммерсантов или просто путешественников, для которых такая карта была бы настоящей находкой, так как существенно облегчила бы навигацию, как морскую, так и воздушную.

В целом эта задача оказалась неразрешимой. Поверхность цилиндра или конуса можно без искажений перенести на плоскость (такие поверхности называются развертывающимися ), отобразить же на плоскость поверхность сферы, сохранив расстояние между любыми двумя точками, невозможно. Дело в том, что даже малую область сферической поверхности (в отличие от цилиндра или конуса) невозможно развернуть на плоскости без трещин, складок или искажений. Любая плоская карта Земли или какой-то ее части непременно будет искажать какие-либо свойства. Поэтому в настоящее время так необходимы карты с минимальными (еще лучше нулевыми) искажениями тех свойств, для передачи которых предназначается карта. Желательно, чтобы и другие свойства деформировались как можно меньше. Всего существует четыре основных типа искажений:

• искажение длин (линии, одинаковые на поверхности Земли, изображаются на карте отрезками разной длины);
• искажение углов (углы на карте между взятыми направлениями не равны горизонтальным углам между теми же направлениями на поверхности земного эллипсоида);
• искажение форм (форма участка или занятой объектом территории на карте отлична от их формы на поверхности Земли);
• искажение площадей (связано с масштабом площади: при постоянстве величины масштаба площади по всей поверхности карты искажения площадей на ней нет).

Помимо классических карт, большая часть которых была разработана в средние века, фантазия ученых предоставляла навигаторам весьма необычные способы проекции земной поверхности, но прежде чем описать способы составления необычных карт, рассмотрим некоторые классические методы картографии.

Центр проекции может быть произвольным по отношению к проецируемой сфере; таким образом, существует бесконечное множество всевозможных различных проекций. Если проводить лучи из некоторой точки, взятой на прямой, проходящей через центр шара перпендикулярно некоторой плоскости, то получим на этой плоскости перспективную проекцию. Рассмотрим некоторые из этих проекций, наиболее полезные с точки зрения картографии.

Стереографическая проекция

Важное свойство любой карты - сохранение углов (угол между любыми двумя линиями на карте должен быть таким же, как угол между прообразами этих линий на земной поверхности). Сохранение углов особенно важно для мореплавания и аэронавтики, так как оно означает, что наблюдаемый угол между любыми двумя ориентирами равен углу, измеряемому на карте с помощью транспортира. Кроме того, на такой карте остаются неизменными и площади малых областей. Карты, сохраняющие углы, называются конформными. Проще всего построить конформную карту с помощью стереографической проекции.

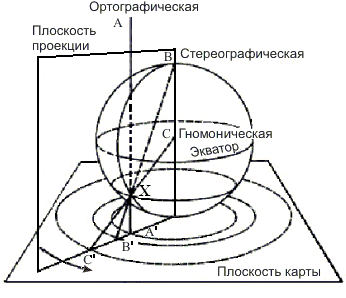
На рис. 7.8 показано, как поверхность сферы в точке проецируется из точки (принадлежащей сфере) на плоскость, касательную к сфере в диаметрально противоположной точке ( антипод точки ). Проекция называется экваториальной, полярной или косой в зависимости от того, где находятся антиподы: на экваторе, полюсах или в какой-нибудь другой точке земной поверхности соответственно. К сожалению, конформность вызывает искажение масштаба, возрастающее с увеличением расстояния от центра карты.

Рис. 7.8. Три проекции

Обозначим за долготу и дополнение до широты точки на сфере буквами и соответственно, , а через и - координаты проекций этой точки в некоторой декартовой системе координат, заданной на плоскости проекции. Соответствующие формулы проецирования для Северного полушария имеют следующий вид:

Гномоническая проекция

Отображение точки из центра земного шара на плоскость карты в точку 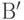порождает гномоническую проекцию (рис. 7.8). Проекция получила такое название, так как она напоминает конструкцию солнечных часов с гномоном. Любая дуга большого круга на поверхности земного шара переходит в прямую на гномонической карте. Большим кругом называется окружность на сфере, плоскость которой проходит через ее центр. Такая карта не обладает конформностью, но навигаторы ценят ее за одно важное свойство, отсутствующее у всех других проекций сферы на плоскость: прямая между любыми двумя точками на гномонической карте является геодезической, или кратчайшей дугой между этими двумя точками, и соответствует дуге большого круга на поверхности Земли.

Ортографическая проекция

Если центр проекции находится в бесконечности (все проецирующие лучи параллельны), то проекция будет ортографической (рис. 7.8). Например, глядя на Луну с Земли, наблюдатель видит Луну практически в ортографической проекции. У края ортографической карты расстояния сильно искажены. Ортографическая карта не сохраняет ни площадей, ни углов, но, выполненная достаточно искусно, создает сильную иллюзию шарообразной Земли. Карты, начерченные с точки зрения наблюдателя, находящегося над земной поверхностью, не точны в передаче многих ее свойств, но наиболее верно соответствуют нашему зрительному восприятию сферы.

Эта проекция получается при проецировании на плоскость, касательную к сфере в центре изображаемого явления 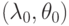, с помощью лучей, перпендикулярных этой плоскости. Формулы этой проекции следующие:

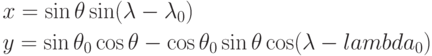
Проекции на цилиндр

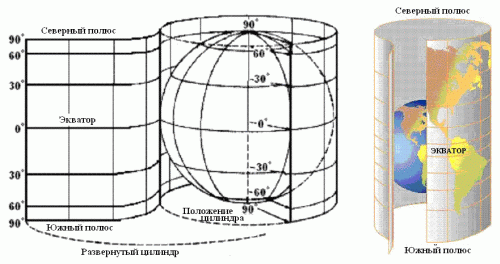
Поверхность сферы также можно проецировать на цилиндры и конусы, "надетые" на сферу. После построения цилиндрической или конической проекции поверхность разрезается и развертывается на плоскость.

Лучи, проецирующие земной шар на цилиндр, выбираются так, чтобы они были параллельны плоскости, высекающей окружность, по которой сфера и цилиндр соприкасаются (рис. 7.9). Если цилиндр касается Земли вдоль экватора, то все меридианы и параллели на карте переходят в прямые, пересекающиеся под прямыми углами.

увеличить изображение
Рис. 7.9. Метод цилиндрической проекции с сохранением площадей

Цилиндрическая карта не всегда обладает конформностью и может сильно искажать расстояния и форму областей. Отметим, что ни одна карта не может одновременно быть конформной и сохранять площади. Было предложено огромное число других проекций, сохраняющих площадь; в современных атласах чаще всего встречаются сохраняющие площади карты, построенные с помощью цилиндрической проекции, которая была предложена Карлом Б.Мольвейде в 1805 г.