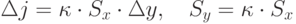Представление геометрической информации
Поверхности свободных форм (функциональные модели)
Характерной особенностью предлагаемого способа задания поверхностей
является то, что основным примитивом здесь является поверхность
второго порядка - квадрик. Он определяется с помощью вещественной
непрерывной функции трех переменных 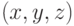 в виде неравенства
в виде неравенства



Свободная форма - это произвольная поверхность, обладающая свойствами гладкости, непрерывности и неразрывности. На базе квадриков строятся свободные формы, которые описывают функциональные модели. Свободная форма, построенная на этих принципах, имеет ряд достоинств, к которым, в первую очередь, надо отнести следующие:
- Легкая процедура расчета координат каждой точки.
- Небольшой объем информации для описания достаточно сложных форм.
- Возможность строить поверхности на основе скалярных данных без предварительной триангуляции.
Этот подход будет более подробно изложен в следующих главах.
В нашем курсе предполагается рассмотреть растровые алгоритмы для изображения таких геометрических примитивов, как отрезки, многоугольники, окружности и эллипсы. Но сначала мы займемся тем геометрическим аппаратом, который позволит адекватно описывать объекты в пространстве, работать с ними и формировать изображение.
Системы координат: мировая, объектная, наблюдателя и экранная
Одной из распространенных задач компьютерной графики является изображение двумерных графиков в некоторой системе координат. Эти графики предназначены для отображения зависимости между переменными, заданной с помощью функции. Например, во второй главе настоящего курса приведен ряд графиков, характеризующих восприятие света глазом человека. Чтобы получить такой график, прикладная программа должна описать различные выходные примитивы (точки, линии, цепочки символов), указав их местоположение и размеры в прямоугольной системе координат. Единицы измерения, в которых задаются эти объекты, зависят от их природы: изменение температуры, например, можно отображать в градусах за час, перемещение тела в пространстве - в километрах в секунду, и т. д. Эти прикладные (или ориентированные на пользователя) координаты позволяют задавать объекты в двумерном или трехмерном мире пользователя, и их принято называть мировыми координатами.
Изображение трехмерных объектов сопряжено с целым рядом задач. Прежде всего надо помнить, что изображение является плоским, поэтому надо добиться адекватной передачи визуальных свойств предметов, дать достаточно наглядное представление о глубине. В дальнейшем группы трехмерных объектов, предназначенных для изображения, будем называть пространственной сценой, а ее двумерное изображение - образом.
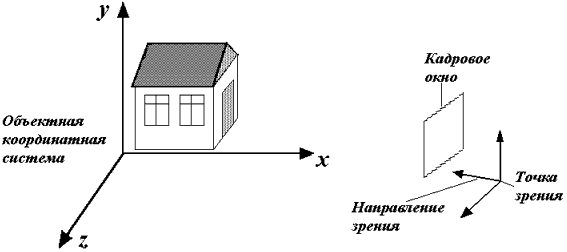
Как и в случае с двумерными объектами, первым шагом построения является ввод информации об объектах. Сцена занимает какое-то определенное место в пространстве, а ее описание привязывается к трехмерной декартовой системе координат, связанной с нею, - объектной координатной системе. Координаты объектов, составляющих сцену, определяются на основе их реальных размеров и взаимного расположения. В зависимости от точки, из которой рассматривается сцена, можно получить множество различных ее образов. Если построено достаточно много таких образов, то по ним можно восстановить объемную структуру предмета. Выбор точки и направления зрения тоже можно описать математически, введя декартову систему координат наблюдателя, начало которой находится в точке обзора, а одна из осей совпадает с направлением зрения (рис. 4.3). Переход от объектных координат к координатам наблюдателя математически реализуется так, как это было описано в третьей главе. На этом этапе преобразований сохраняются реальные размеры объектов.
Видимый образ формируется на некоторой плоскости, которую в дальнейшем будем называть картинной плоскостью. Способы преобразования трехмерного объекта в двумерный образ ( проекции ) могут быть различными. Так или иначе, но полученный образ также должен быть описан в некоторой двумерной системе координат. В зависимости от способа его получения реальные размеры образа также могут быть различны. Различные виды проецирования будут подробно рассмотрены в последующих главах.
Поскольку нашей конечной целью является получение изображения на экране, то перенесение образа сопровождается изменением масштаба в соответствии с размерами экрана. Обычно началом координат в системе координат образа считается левый нижний угол листа с изображением. На экране дисплея начало координат традиционно находится в левом верхнем углу. Отображение рисунка с картинной плоскости на экран должно производиться с минимальным искажением пропорций, что само по себе вносит ограничение на область экрана, занимаемую рисунком. Изменение масштаба должно осуществляться с сохранением пропорций области (рис. 4.4).
Объекты в системе координат картинной плоскости задаются в каких- либо единицах измерения, причем масштаб одинаков по обеим осям координат. На экране единицей измерения является пиксель, который следует рассматривать как прямоугольный, поэтому масштабы по горизонтальной и вертикальной осям могут быть различны, что необходимо учитывать при задании коэффициентов масштабирования.
Рассмотрим ситуацию, когда изображение занимает на картинной
плоскости прямоугольную область  . При отображении рисунка на экран
каждая точка исходного прямоугольника с координатами
. При отображении рисунка на экран
каждая точка исходного прямоугольника с координатами  перейдет в
некоторую точку с целочисленными координатами
перейдет в
некоторую точку с целочисленными координатами  . Введем
обозначения:
. Введем
обозначения:
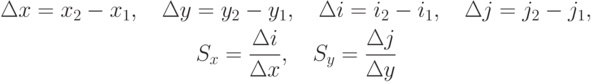
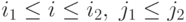 ).
Определим преобразование координат образа
).
Определим преобразование координат образа  в экранные координаты
в экранные координаты  формулами
формулами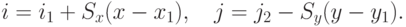

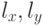 - горизонтальный и вертикальный размер одного пикселя. Эти
параметры легко установить, зная размеры экрана и разрешение. Отсюда
получаем
- горизонтальный и вертикальный размер одного пикселя. Эти
параметры легко установить, зная размеры экрана и разрешение. Отсюда
получаем