Потоки в сетях
Потоки в сетях
Деятельность современного общества тесно связана с разного рода сетями — возьмите, к примеру, транспорт, коммуникации, распределение товаров и тому подобное. Поэтому математический анализ таких сетей стал предметом фундаментальной важности.
Определим сеть  как орграф, каждой дуге
как орграф, каждой дуге  которого приписано неотрицательное действительное число
которого приписано неотрицательное действительное число  ,
называемое ее пропускной способностью. Другое определение сети,
эквивалентное первому, звучит так: сеть представляет собой
пару
,
называемое ее пропускной способностью. Другое определение сети,
эквивалентное первому, звучит так: сеть представляет собой
пару 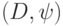 , где
, где  — орграф, а
— орграф, а  — функция,
отображающая множество дуг орграфа
— функция,
отображающая множество дуг орграфа  в множество неотрицательных действительных чисел. Полустепень
исхода
в множество неотрицательных действительных чисел. Полустепень
исхода 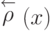 вершины
вершины  определяется тогда как сумма пропускных
способностей дуг вида
определяется тогда как сумма пропускных
способностей дуг вида 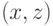 ,
и аналогичным образом определяется полустепень
захода
,
и аналогичным образом определяется полустепень
захода 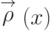 .
Аналог орлеммы о рукопожатиях принимает
следующий вид: сумма полустепеней исхода всех вершин в сети равна
сумме их полустепеней захода. В дальнейшем будем предполагать (если не
оговорено иное), что орграф
.
Аналог орлеммы о рукопожатиях принимает
следующий вид: сумма полустепеней исхода всех вершин в сети равна
сумме их полустепеней захода. В дальнейшем будем предполагать (если не
оговорено иное), что орграф  содержит ровно один
источник
содержит ровно один
источник  и один сток
и один сток  ; общий случай, когда имеется несколько источников
и стоков, легко свести к этому частному.
; общий случай, когда имеется несколько источников
и стоков, легко свести к этому частному.
Для данной сети 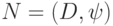 определим поток
через
определим поток
через  как функцию
как функцию  , составляющую каждой дуге
, составляющую каждой дуге  из
из  неотрицательное действительное число
неотрицательное действительное число 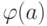 (называемое потоком через
(называемое потоком через  ) таким образом, что
) таким образом, что 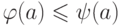 для любой дуги
для любой дуги  ; по отношению к сети
; по отношению к сети 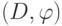 полустепень исхода и полустепень захода любой вершины (отличной от
полустепень исхода и полустепень захода любой вершины (отличной от  и
и  ) равны между собой. Рассуждая неформально, это означает, что поток
через любую дугу не превосходит ее пропускной способности и что "полный
поток", входящий в любую вершину (отличную от
) равны между собой. Рассуждая неформально, это означает, что поток
через любую дугу не превосходит ее пропускной способности и что "полный
поток", входящий в любую вершину (отличную от  и
и  ), равен
"полному потоку", выходящему из нее. Другим потоком является нулевой поток, при котором
поток через каждую дугу равен нулю (любой другой поток называется нулевым).
), равен
"полному потоку", выходящему из нее. Другим потоком является нулевой поток, при котором
поток через каждую дугу равен нулю (любой другой поток называется нулевым).
Для удобства назовем дугу  , для которой
, для которой  , насыщенной ; остальные дуги называются ненасыщенными. Из орлеммы о рукопожатиях следует, что сумма
потоков через дуги, инцидентные
, насыщенной ; остальные дуги называются ненасыщенными. Из орлеммы о рукопожатиях следует, что сумма
потоков через дуги, инцидентные  , равна сумме потоков через дуги,
инцидентные
, равна сумме потоков через дуги,
инцидентные  ; эта сумма называется величиной потока.
Будем в первую очередь интересоваться потоками, имеющими наибольшую
возможную величину, — так называемыми максимальными потоками.
Заметим, что в общем случае сеть может иметь несколько различных
максимальных потоков, однако их величины должны совпадать.
; эта сумма называется величиной потока.
Будем в первую очередь интересоваться потоками, имеющими наибольшую
возможную величину, — так называемыми максимальными потоками.
Заметим, что в общем случае сеть может иметь несколько различных
максимальных потоков, однако их величины должны совпадать.
Изучение максимальных потоков через сеть 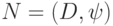 тесно связано
с понятием разреза, т.е. такого множества
тесно связано
с понятием разреза, т.е. такого множества  дуг
орграфа
дуг
орграфа  , которое обладает тем свойством, что любая простая орцепь из
, которое обладает тем свойством, что любая простая орцепь из  в
в  проходит через дугу, принадлежащую
проходит через дугу, принадлежащую  . Другими
словами, разрезом в
сети является не что иное, как
. Другими
словами, разрезом в
сети является не что иное, как 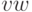 — разделяющее
множество соответствующего орграфа
— разделяющее
множество соответствующего орграфа  . Пропускной способностью
разреза называется сумма пропускных способностей принадлежащих ему дуг.
Мы будем рассматривать главным образом такие разрезы, которые обладают
наименьшей возможной пропускной способностью, — так называемые минимальные разрезы.
. Пропускной способностью
разреза называется сумма пропускных способностей принадлежащих ему дуг.
Мы будем рассматривать главным образом такие разрезы, которые обладают
наименьшей возможной пропускной способностью, — так называемые минимальные разрезы.
Величина любого потока не превышает пропускной способности любого разреза, и, следовательно, величина любого максимального потока не превышает пропускной способности любого минимального разреза. Однако сразу не ясно, что два последних числа всегда равны между собой; этот замечательный результат называется теоремой о максимальном потоке и минимальном разрезе. Впервые она была доказана Фордом и Фалкерсоном в 1955,г. Мы приведем здесь два доказательства; первое из них показывает, что эта теорема по существу эквивалентна теореме Менгера, а второе является прямым доказательством.

