Гамильтоновы графы

Гамильтоновы графы

Рассмотрим проблему существования замкнутой цепи, проходящей ровно один раз через каждую вершину графа .

Примеры:

Ясно, что такая цепь должна быть циклом, исключая тривиальный случай, когда является графом . Если такой цикл существует, то он называется гамильтоновым циклом (путем), а называется гамильтоновым графом. Граф, который содержит простую цепь, проходящую через каждую его вершину, называется полугамильтоновым. Название "гамильтонов цикл" возникло в связи с тем, что Уильям Гамильтон занимался исследованием существования таких циклов в графе, соответствующем додекаэдру. Додекаэдр — это многогранник, гранями которого служат 12 правильных пятиугольников. У него 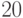вершин и ребер.

Эйлеровы и гамильтоновы пути сходны по способу задания. Первые содержат все ребра, по одному разу каждое, вторые - все вершины, по одному разу каждую. Но, несмотря на внешнее сходство, задачи их поиска резко отличаются по степени трудности. Для решения вопроса о наличии эйлерова цикла в графе достаточно выяснить, все ли его вершины четны. Критерий же существования гамильтонова цикла в произвольном графе еще не найден. Решение этой проблемы имеет практическую ценность, так как к игре Гамильтона близка известная задача о коммивояжере, который должен объехать несколько пунктов и вернуться обратно. Он обязан побывать в каждом пункте в точности по одному разу и заинтересован в том, чтобы затратить на поездку как можно меньше времени. А для этого требуется определить все варианты посещения городов и подсчитать в каждом случае затрату времени. По своей математической постановке игра Гамильтона близка к задаче о порядке переналадки станков, задаче о подводке электроэнергии к рабочим местам и т.д. (Подробнее об этом рассказывается, например, в книге В.И.Мудрова "Задача о коммивояжере" М.: Знание, 1969).

Рассмотрим несколько достаточных условий существования гамильтоновых циклов в графе.

Во-первых, всякий полный граф является гамильтоновым. Действительно, он содержит такой простой цикл, которому принадлежат все вершины данного графа. Во-вторых, если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие ребра, то он также является гамильтоновым.

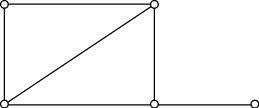
Пример.

Простой (гамильтонов) цикл выделен сплошной линией 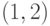, , 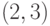, , 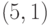. Заметим, что если граф имеет один гамильтонов цикл, то он может иметь и другие гамильтоновы циклы.

Если гамильтонов граф объединить с еще одной вершиной ребром так, что образуется висячая вершина, то такой граф гамильтоновым не является, поскольку не содержит простого цикла, проходящего через все вершины графа.

Пример.

Не является гамильтоновым и граф, представляющий собой простой цикл с "перекладиной", на которой расположены одна или несколько вершин.