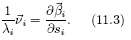Сложные поверхности и основы планирования управления роботом-станком для их воспроизведения

Сложные поверхности

При создании системы управления процессом механической обработки деталей с использованием многозвенных манипуляционных механизмов возникает необходимость экономного описания этого процесса, в том числе описания геометрического контура обрабатываемой поверхности. При этом следует отметить, что метод описания геометрии обрабатываемой поверхности определяет принципы построения систем управления манипуляционными механизмами, а такжесистемы распознавания геометрических параметров. Геометрия обрабатываемой поверхности определяет также требуемое количество степеней подвижности манипулятора, необходимое для выполнения данной операции.

Поверхности реальных машиностроительных деталей

Поверхности реальных машиностроительных деталей, имеющих сферическую, цилиндрическую, коническую или иную форму, могут быть заданы следующими параметрами: радиусами кривизны, кручения и координатами опорных точек или линий. Перемещение инструмента по траектории на обрабатываемой поверхности от одной опорной точки к другой может быть задано как перемещение по траектории с заданными радиусами кривизны и кручения.

Форма поверхности образуется режущей кромкой инструмента, который перемещается по траектории на обрабатываемой детали. Эта траектория выбирается таким образом, чтобы при движении по ней режущей кромки инструмента образовывалась требуемая поверхность.

Рис. 11.1.

При движении инструмента по траектории, расположенной на поверхности обрабатываемой детали (рис. 11.1), ось сопровождающего трехгранника (трехгранника Фрэне) 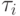направлена по касательной к траектории, 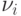— по нормали, а 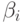— по бинормали к поверхности, на которой расположена траектория. Основные параметры, характеризующие траекторию в пространстве, — это текущие линейные координаты траектории, радиус кривизны 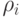и радиус кручения 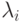. Радиус кривизны 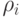в i-й точке траектории направлен вдоль оси 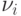и определяется как производная вектора по дуге s_i

Величина радиуса кривизны 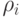в каждой i-й точке поверхности вычисляется через модуль производной

Цилиндрическая поверхность полностью может быть задана координатами опорных точек траектории, радиусами кривизны 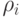и направляющими косинусами осе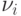й и 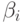, причем для цилиндрической поверхности направляющие косинусы оси 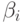постоянны для всех опорных точек.

Радиус кручения 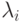(рис. 11.1) также направлен по оси 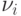и определяется как производная вектора по дуге s_i

Величина радиуса кручения 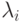в каждой i-й опорной точке поверхности вычисляется через модуль производной

При одновременном повороте с заданными радиусами кривизны 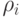и кручения 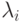получается произвольная форма обрабатываемой поверхности.