НОУ ИНТУИТ | Интеллектуальные робототехнические системы. Лекция 11: Сложные поверхности и основы планирования управления роботом-станком для их воспроизведения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 18.05.2005 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 48 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Задача 2

Задача 2 состоит в определении углов ориентации трехгранника 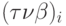$(\tau \nu \beta )_{i}$ относительно осей системы координат (XYZ)_д. Для каждой i-й точки поверхности, используя уравнение (11.9), кроме текущих координат поверхности, вычисляются направляющие косинусы для осей трехгранника 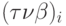$(\tau \nu \beta )_{i}$ , связанного с поверхностью, которые представляют соответственно касательную, нормаль и бинормаль в каждой точке поверхности.

Для нахождения углов ориентации сопровождающего трехгранника 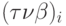$(\tau \nu \beta )_{i}$ в каждой точке траектории относительно осей системы координат (XYZ)_д необходимо получить уравнение нормали в точке поверхности, касательной к траектории перемещения инструмента относительно детали, и уравнение бинормали.

Направляющие косинусы нормали (ось 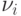$\nu _{i}$ ) к поверхности в каждой точке траектории x_iy_iz_i определяются из уравнения (11.9)

С учетом (11.10) направляющие косинусы для оси 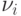$\nu _{i}$ в точке поверхности относительно осей системы координат (XYZ)_д принимают вид

Направляющие косинусы для касательной (ось 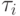$\tau _{i}$ ) к траектории движения инструмента относительно детали определяется через частные производные от x, y, z по времени в i-й точке

С учетом (11.12) получим

Направляющие косинусы для бинормали трехгранника 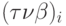$(\tau \nu \beta )_{i}$ — (ось 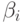$\beta _{i}$ ) определяются из векторного произведения

Таким образом, уравнения (11.11), (11.13) и (11.14) определяют ориентацию подвижного трехгранника 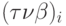$(\tau \nu \beta )_{i}$ относительно осей системы координат (XYZ)_д.

Задача 3

Задача 3 состоит в нахождении элементов матрицы ^дA_i (рис. 9.5), определяющей закон перемещения инструмента относительно детали. Элементы матрицы ^дA_i

находятся на основе решения задач 1 и 2. Координаты x_i, y_i, z_i представляют переменные x, y и z в полиноме Лагранжа (11.7), вычисляемые для каждой i-й точки траектории перемещения инструмента по поверхности детали. Направляющие косинусы 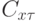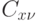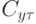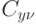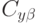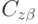$C_{x\tau }$ , $C_{x\nu }$ , $C_{x\beta }$ , $C_{y\tau }$ , $C_{y\nu }$ , $C_{y\beta }$ , $C_{z\tau }$ , $C_{z\nu }$ , $C_{z\beta }$ определяются из уравнений (11.11), (11.13) и (11.14).

Для получения непрерывного перемещения по планируемой траектории с заданной скоростью V_п (рис. 11.3) ее координаты x и z задаются в параметрическом виде

x(t)=V_xt, z(t)=V_zt,

где скорости V_x и V_z для текущего шага вычисляются через значение V_п на предыдущем шаге

V_x=C_x V_п, V_Z=C_zV_п.

Значения C_x и C_z определяются также на предыдущем шаге.

Подстановкой текущих координат x(t), z(t) в (11.9) вычисляется координата y(t) планируемой точки траектории, а также планируемые значения направляющих косинусов 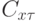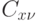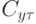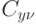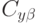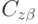$C_{x\tau }$ , $C_{x\nu }$ , $C_{x\beta }$ , $C_{y\tau }$ , $C_{y\nu }$ , $C_{y\beta }$ , $C_{z\tau }$ , $C_{z\nu }$ , $C_{z\beta }$ . Текущие элементы ^дA_i вычисляются для каждой точки траектории с частотой задания координат x(t) и z(t).

Таким образом, метод, основанный на применении сопровождающего трехгранника, в сочетании с описанием обрабатываемой поверхности детали полиномами Лагранжа позволяет планировать закон перемещения инструмента и его ориентацию относительно детали для получения поверхностей, задаваемых координатами опорных точек.

Дальше >>

Интеллектуальные робототехнические системы

Сложные поверхности и основы планирования управления роботом-станком для их воспроизведения

Задача 2

Задача 3

Вопросы и ответы

Студенты

Авторизоваться

Интеллектуальные робототехнические системы

Сложные поверхности и основы планирования управления роботом-станком для их воспроизведения

Задача 2

Задача 3

Вопросы и ответы

Студенты