| Возможность получения документа о прохождении курса |
Кратчайшие пути
Кратчайшие пути
В этой лекции рассматриваются связные графы с неотрицательными весами
ребер. Вес пути в графе определяется как сумма весов ребер этого пути.
Кратчайшим путем между двумя вершинами называется путь наименьшего веса,
соединяющий эти вершины. Рассмотрим задачу отыскания кратчайших путей от
заданной вершины  до всех остальных вершин графа. Возможно, более
естественной постановкой задачи кажется поиск кратчайшего пути между двумя
заданными вершинами. Однако в настоящее время не известно никакого способа
решения этой задачи, существенно лучшего, чем поиск кратчайших путей от
начальной вершины до всех остальных.
до всех остальных вершин графа. Возможно, более
естественной постановкой задачи кажется поиск кратчайшего пути между двумя
заданными вершинами. Однако в настоящее время не известно никакого способа
решения этой задачи, существенно лучшего, чем поиск кратчайших путей от
начальной вершины до всех остальных.
Геодезическое дерево
Пусть  - вершина связного графа
- вершина связного графа  с
заданной на
множестве ребер весовой функцией
с
заданной на
множестве ребер весовой функцией  с неотрицательными
значениями. Каркас
с неотрицательными
значениями. Каркас  графа
графа  с корнем
с корнем  называется геодезическим
деревом, если для любой
вершины
называется геодезическим
деревом, если для любой
вершины  путь между вершинами
путь между вершинами  и
и  в дереве
в дереве  является кратчайшим путем между этими вершинами
в графе
является кратчайшим путем между этими вершинами
в графе  .
Это обобщает понятие геодезического дерева, введенное в
"лекции 4"
и соответствующее случаю, когда все веса равны 1. Докажем сначала, что
геодезическое дерево всегда существует.
.
Это обобщает понятие геодезического дерева, введенное в
"лекции 4"
и соответствующее случаю, когда все веса равны 1. Докажем сначала, что
геодезическое дерево всегда существует.
Обозначим через  вес кратчайшего пути между
вершинами
вес кратчайшего пути между
вершинами  и
и  в графе
в графе  . Дерево
. Дерево  с корнем
с корнем  назовем частичным
геодезическим деревом, (ЧГД), если существует
такое геодезическое дерево
назовем частичным
геодезическим деревом, (ЧГД), если существует
такое геодезическое дерево  с корнем
с корнем  ,
что
,
что  является подграфом дерева
является подграфом дерева  . Иначе говоря, ЧГД - это
корневое
дерево, которое можно достроить до геодезического дерева с тем же корнем.
. Иначе говоря, ЧГД - это
корневое
дерево, которое можно достроить до геодезического дерева с тем же корнем.
Пусть  - множество всех вершин графа
- множество всех вершин графа  .
Для множества
.
Для множества  через
через 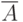 обозначаем дополнение
обозначаем дополнение  до
до  .
.
Теорема 1. Пусть  - ЧГД с корнем
- ЧГД с корнем  и множеством вершин
и множеством вершин  в графе
в графе  ,
, 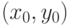 - ребро c наименьшим
значением величины
- ребро c наименьшим
значением величины  среди
всех ребер
среди
всех ребер  , где
, где 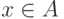 ,
, 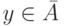 .
Тогда
.
Тогда  - ЧГД
с корнем
- ЧГД
с корнем  .
.
Доказательство.
Рассмотрим в дереве 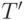 путь
путь 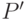 ,
соединяющий вершину
,
соединяющий вершину 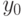 с корнем
с корнем  . Он состоит из
пути между
вершинами
. Он состоит из
пути между
вершинами  и
и 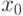 в дереве
в дереве  и
ребра
и
ребра 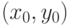 ,
следовательно, .
,
следовательно, .
 |
( 1) |
Мы должны доказать, что он является кратчайшим путем между
вершинами  и
и 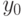 в графе
в графе  . Допустим, имеется путь
. Допустим, имеется путь  между этими вершинами, такой, что.
между этими вершинами, такой, что.
 |
( 2) |
Пусть  - первое ребро пути
- первое ребро пути  , у которого
, у которого 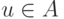 ,
, 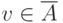 (считаем, что путь начинается в
вершине
(считаем, что путь начинается в
вершине  ). Так как
веса ребер неотрицательны, то
). Так как
веса ребер неотрицательны, то
 |
( 3) |
Из (1), (2) и (3) следует неравенство 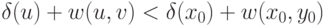 , противоречащее выбору
ребра
, противоречащее выбору
ребра 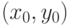 .
.
Эта теорема показывает, что геодезическое дерево можно построить с помощью следующего алгоритма.
Алгоритм 1. Построение геодезического дерева для
вершины  .
.
- cоздать дерево
 из одной вершины
из одной вершины 
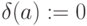

-
while
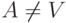 do
do
- cреди ребер
 , где
, где 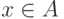 ,
,  , найти
ребро
, найти
ребро 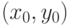 c наименьшим значением величины
c наименьшим значением величины  ;
; - добавить к дереву
 вершину
вершину 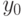 и
ребро
и
ребро 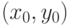 ;
; 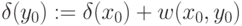
Этот алгоритм очень похож на алгоритм Прима для построения оптимального
каркаса. Единственное отличие между ними состоит в правиле выбора ребра,
присоединяемого к строящемуся дереву на очередном шаге. В алгоритме Прима
выбирается ребро наименьшего веса, а в алгоритме для построения
геодезического дерева - ребро с минимальным значением величины  . Ясно, что и оценка трудоемкости нового
алгоритма будет
такая же, как и для алгоритма Прима, то есть
. Ясно, что и оценка трудоемкости нового
алгоритма будет
такая же, как и для алгоритма Прима, то есть 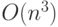 . Подобно
алгоритму Прима, этот алгоритм можно рационализировать, понизив тем самым
оценку трудоемкости до
. Подобно
алгоритму Прима, этот алгоритм можно рационализировать, понизив тем самым
оценку трудоемкости до 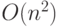 . Усовершенствованный алгоритм
поиска
кратчайших путей известен как алгоритм Дейкстры.
. Усовершенствованный алгоритм
поиска
кратчайших путей известен как алгоритм Дейкстры.
