| Возможность получения документа о прохождении курса |
Рационализация переборных алгоритмов
Рационализация поиска наибольшего независимого множества
Известны различные приемы сокращения перебора при использовании описанной
стратегии исчерпывающего поиска. Один из них основан на следующем
наблюдении. Допустим, в графе  , для которого нужно найти
наибольшее независимое множество, имеются две вершины
, для которого нужно найти
наибольшее независимое множество, имеются две вершины  и
и  , такие, что каждая вершина, отличная от
, такие, что каждая вершина, отличная от  и
смежная
с вершиной
и
смежная
с вершиной  , смежна и с вершиной
, смежна и с вершиной  . Иначе говоря,
. Иначе говоря,  . Будем говорить в этом случае,
что вершина
. Будем говорить в этом случае,
что вершина  поглощает вершину
поглощает вершину  .
Если при этом вершины
.
Если при этом вершины  и
и  смежны, то скажем,
что вершина
смежны, то скажем,
что вершина  смежно поглощает вершину
смежно поглощает вершину  .
Вершину
.
Вершину  в этом случае назовем смежно поглощающей.
Например, в графе, изображенном на рис. 11.1,
вершина 2 смежно поглощает
вершины 1 и 3. Вершины 5 и 6 в этом графе тоже являются смежно
поглощающими.
в этом случае назовем смежно поглощающей.
Например, в графе, изображенном на рис. 11.1,
вершина 2 смежно поглощает
вершины 1 и 3. Вершины 5 и 6 в этом графе тоже являются смежно
поглощающими.
Теорема 1. Если вершина  является смежно
поглощающей в графе
является смежно
поглощающей в графе  , то
, то 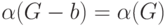 .
.
Доказательство. Допустим, вершина  смежно поглощает
вершину
смежно поглощает
вершину  в графе
в графе  . Пусть
. Пусть  -
наибольшее
независимое множество графа
-
наибольшее
независимое множество графа  . Если
. Если  не содержит
вершину
не содержит
вершину  ,
то оно является наибольшим независимым множеством и в графе
,
то оно является наибольшим независимым множеством и в графе  , так что в этом случае
, так что в этом случае 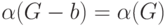 .
Предположим,
что множество
.
Предположим,
что множество  содержит вершину
содержит вершину  . Тогда ни одна
вершина
из множества
. Тогда ни одна
вершина
из множества 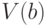 не принадлежит
не принадлежит  . Значит,
. Значит,  не содержит вершину
не содержит вершину  и ни одну вершину из
множества
и ни одну вершину из
множества 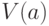 .
Но тогда множество
.
Но тогда множество 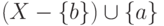 тоже будет независимым,
причем оно целиком содержится в графе
тоже будет независимым,
причем оно целиком содержится в графе  , а число элементов в
нем
такое же, как в множестве
, а число элементов в
нем
такое же, как в множестве  . Значит, и в этом
случае
. Значит, и в этом
случае 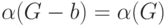 .
.
Итак, если мы удалим из графа смежно поглощающую вершину  ,
то получим граф с тем же числом независимости. Так как новый граф является
порожденным подграфом исходного графа
,
то получим граф с тем же числом независимости. Так как новый граф является
порожденным подграфом исходного графа  , то каждое наибольшее
независимое множество нового графа будет наибольшим независимым множеством
исходного. Этот прием называется "сжатием по включению".
Исследование
применимости и применение операции сжатия по включению к каждому
встречающемуся подграфу требуют, конечно, дополнительных расходов времени
(каких?), но могут привести к существенному сокращению дерева подзадач.
Для некоторых графов задача о независимом множестве может быть решена
с помощью одних только сжатий по включению. Таков, например,
граф
, то каждое наибольшее
независимое множество нового графа будет наибольшим независимым множеством
исходного. Этот прием называется "сжатием по включению".
Исследование
применимости и применение операции сжатия по включению к каждому
встречающемуся подграфу требуют, конечно, дополнительных расходов времени
(каких?), но могут привести к существенному сокращению дерева подзадач.
Для некоторых графов задача о независимом множестве может быть решена
с помощью одних только сжатий по включению. Таков, например,
граф 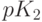 ,
и вообще любой лес. Действительно, любая вершина, смежная с листом,
поглощает этот лист. Рассмотрим более широкий класс графов, для которых
этот прием эффективен.
,
и вообще любой лес. Действительно, любая вершина, смежная с листом,
поглощает этот лист. Рассмотрим более широкий класс графов, для которых
этот прием эффективен.