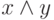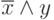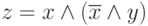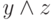НОУ ИНТУИТ | Введение в информатику. Лекция 5: Высказывания и предикаты

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2006 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 123 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Три базовые операции алгебры предикатов определяются таблицей их значений, так как в алгебре предикатов из-за дискретности значений логических функций часто используется табличная форма задания функции. Булеву функцию n переменных можно полностью определить таблицей из 2ⁿ строк.

Итак, эти операции определяются совмещенной таблицей значений вида

		$\overline{x}$	$x\land y$	$x\lor y$
0	0	1	0	0
0	1	1	0	1
1	0	0	0	1
1	1	0	1	1

Такая таблица всех значений некоторой логической функции называется таблицей истинности этой функции.

Пример. Составим таблицу истинности функции 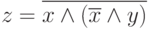$z=\overline{x\land(\overline{x}\land y)}$ . Эта таблица имеет вид

		$\overline{x}$	$\overline{x}\land y$	$z=x\land(\overline{x}\land y)$	$z=\overline{x\land(\overline{x}\land y)}$
0	0	1	0	0	1
0	1	1	1	0	1
1	0	0	0	0	1
1	1	0	0	0	1

Следовательно, функция тождественно-истинна. Это можно было доказать (проверить) и с помощью аксиом:

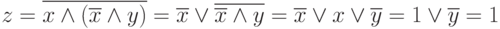
$z=\overline{x\land(\overline{x}\land y)}=\overline{x}\lor\overline{\overline{x}\land y}=\overline{x}\lor x\lor\overline{y}=1\lor\overline{y}=1$

Пример. Заполним таблицу истинности трехместной логической функции 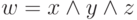$w = x\land y\land z$ . Эта таблица имеет вид

			$y\land z$
0	0	0	0	0
0	0	1	0	0
0	1	0	0	0
1	0	0	0	0
0	1	1	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

Пример. Изобразим графически множество истинности двухместного предиката вида р(х,у) = "модуль числа х равен модулю числа у", если задана область изменения аргументов: $х,у \in [0;1]$ . Имеем соотношение

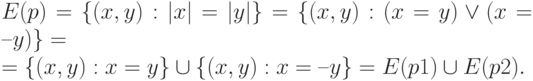
$E(p)=\{(x,y):|x|=|y|\}=\{(x,y):(x=y)\lor(x=–y)\}=\\=\{(x,y ):x=y\}\cup\{(x,y) : x = –y\} = E(p1)\cup E(p2).$

Смысл предикатов р1(х,у) и р2(х,у) очевиден. Множество изображается графиком функции y=|x|, который дан на рис. 5.1:

Рис. 5.1. График функции y = |x|

Кроме указанных трех базовых операций можно с их помощью ввести еще следующие важные операции алгебры предикатов (можно их назвать небазовыми операциями):

импликации: $(x\to y)\equiv(\overline{x}\lor y)$ ;
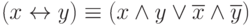эквиваленции: $(x\leftrightarrow y)\equiv(x\land y\lor\overline{x}\land\overline{y})$ .

Операции импликации и эквиваленции, хотя и являются часто используемыми, но не базовые, ибо они определяемы через три введенные выше базовые операции. Нетрудно определить их таблицы истинности (проделайте это самостоятельно с помощью правых частей приведенных равенств).

При выполнении логических операций в компьютере они сводятся к поразрядному сравнению битовых комбинаций. Эти операции достаточно быстро (аппаратно) выполняемы, так как сводятся к выяснению совпадения или несовпадения битов.

В логических формулах определено старшинство операций, например: скобки, отрицание, конъюнкция, дизъюнкция (остальные, небазовые операции пока не учитываем).

Всегда истинные формулы называют тавтологиями.

Логические функции эквивалентны, если совпадают их таблицы истинности, то есть совпадают области определения и значения, а также сами значения функции при одних и тех же наборах переменных из числа всех допустимых значений. Если это совпадение происходит на части множества допустимых значений, то формулы называются эквивалентными лишь на этой части (на этом подмножестве).

Задача упрощения логического выражения состоит в преобразовании его к более простому (по числу переменных, операций или операндов) эквивалентному выражению. Наиболее простой вид получается при сведении функции к постоянной – 1 ( истина ) или 0 ( ложь ).

Пример. Упростим:

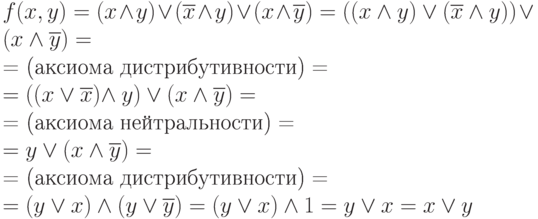
$f(x,y)=(x\land y)\lor(\overline{x}\land y)\lor(x\land\overline{y})=\left((x\land y)\lor(\overline{x}\land y)\right)\lor(x\land\overline{y})=\\ \mbox{= (аксиома дистрибутивности) =}\\ =\left((x\lor\overline{x})\land \right y)\lor(x\land\overline{y})=\\ \mbox{= (аксиома нейтральности) = }\\ =y\lor(x\land\overline{y})=\\ \mbox{= (аксиома дистрибутивности) =}\\=(y\lor x)\land(y\lor\overline{y})=(y\lor x)\land 1=y\lor x=x\lor y$

Задача доказательства равенства двух логических выражений (функций) состоит в установлении эквивалентности этих функций на некотором множестве значений всех переменных, входящих в данную функцию.

Пример. Докажем равенство логических выражений: 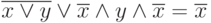$\overline{x\lor y}\lor\overline{x}\land y\land\overline{x}=\overline{x}$ Используя аксиомы алгебры предикатов, получаем равенства

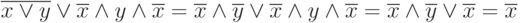
$\overline{x\lor y}\lor\overline{x}\land y\land\overline{x}=\overline{x}\land\overline{y}\lor\overline{x}\land y\land\overline{x}=\overline{x}\land\overline{y}\lor\overline{x}=\overline{x}$

Левая часть равенства приведена к правой части, то есть данное равенство доказано полностью.

Такие задачи решаются с помощью аксиом алгебры предикатов одним из следующих способов:

правая часть равенства приводится к левой части;
левая часть равенства приводится к правой части;
обе части равенства приводятся к третьему выражению.

Логические функции позволяют эффективно решать так называемые инфологические (информационно-логические) задачи, доказывать утверждения.

Дальше >>

Введение в информатику

Высказывания и предикаты

Вопросы и ответы

Студенты

Авторизоваться

Введение в информатику

Высказывания и предикаты

Вопросы и ответы

Студенты