НОУ ИНТУИТ | Введение в информатику. Лекция 12: Формальные языки и грамматики

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2006 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 123 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Аннотация: Рассматриваются основные сведения о формальных и естественных языках, грамматиках, типах грамматик, грамматическом анализе, переводе с языков, типах трансляторов.

Ключевые слова: язык, метаязык, формальный язык, грамматика, трансляция, очередь, синтаксис, семантика, значение, объект, отображение, целое число, аксиома, Паскаль, операции, алфавит, произвольное, подмножество, естественный язык, формальная грамматика, грамматический анализ, нетерминальный символ, отношение, слово, группа, определение, Дополнение, выражение, вычисление, программирование, деление, программа, транслятор, алгоритм, память, работ, компиляция, интерпретация, модуль, исполнение

Математический язык как форма выражения научного знания использовался еще в древности при решении практических задач.

Большую роль в развитии математики как языка – метаязыка наук – сыграла математическая логика, аксиоматизировавшая ряд теории, изучившая их логику, внутреннюю структуру.

Развитие информатики, особенно таких ее разделов, как теория формальных языков, грамматик, структур, алгоритмических языков и методов трансляции баз данных и знаний и других приводит к развитию, углублению, формализации и структурированию предметов наук.

В свою очередь, появилась возможность моделирования языковых структур, формализации, структурирования ряда языков общения, анализа и построения различного рода текстов и словарей, в том числе – их автоматического построения.

Язык, определенный с помощью алфавита (над алфавитом) X = {x₁, x₂, ... , x_n} , – это некоторая устная, звуковая, письменная или иная форма выражения слов над X, включая синтаксис – правила образования структур из слов и словосочетаний, семантику – правила проверки правильности, смысловой однозначности и совместимости синтаксических конструкций языка, состоящих из лексем. Для устных языков (общения) нужна и фонетика – правила произношения составных частей предложения, то есть фонем.

Язык как коммуникативный аппарат должен иметь определяющие конструкции слов над данным алфавитом, грамматические правила образования предложений из слов и соотнесения этих предложений тем явлениям и процессам, которые они описывают, или синтаксическим и семантическим правилам.

Пример. В частности, семантика изучает связи вида:

"знак, структура знаков $\Longleftrightarrow$ значение $\Longleftrightarrow$ объект";

синтаксис – связи вида:

"знак, структура знаков $\Longleftrightarrow$ объект".

Основные функции любого языка – отображение, передача, сжатие, хранение, актуализация информации с помощью сообщений на этом языке.

Пример. Запишем более кратко, сжато, точно (формализованно) факт "целое число x делится на целое число y без остатка". На математическом языке это будет иметь вид "Число x кратно числу y ". Факт, что числа x, y – целые, уже можно специально, как выше, не оговаривать, так как математическое понятие кратности это уже предполагает (аксиома). Запишем еще более кратко и формализованно на алгоритмическом языке Паскаль: " x mod y = 0 ". Здесь уже условие кратности область изменения аргументов не нужно оговаривать – они декларированы в языке Паскаль (в описаниях типов и операции mod ).

Языки бывают естественного происхождения (например языки общения) и искусственного происхождения или формальные языки, разрабатываемые для общения человека с автоматом (компьютером) либо для описания и получения знаний.

Пусть X – некоторый алфавит, X = {x₁, x₂, ... , x_n} , а S(X) – множество слов над алфавитом X, тогда S(X) – бесконечное и счетное множество.

Формальный язык L(X) – произвольное подмножество S(X).

Формальный язык использует естественный язык как лексическую форму оформления входящих в него абстрактных объектов, как метаязык или язык для описания синтаксиса другого языка. Описываемый метаязыком язык в этом случае называется объектным языком (по отношению к метаязыку ).

Формальная грамматика G состоит из совокупностей: T = {t₁, t₂, ... , t_k} – множество терминальных символов языка или множество основных понятий языка ; N = {n₁, n₂, ..., n_m} – множество нетерминальных символов языка или вспомогательных понятий, обозначений конкретных классов слов, например, глаголов или предлогов, причем во множестве N содержится n₀ – начальный символ из N ; P = {p₁, p₂, ..., p_q} – система подстановок (продукции) слов вида 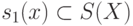$s_{1}(x)\subset S(X)$ в слова 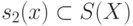$s_{2}(x)\subset S(X)$ или замен всех слов s₁(x) в рассматриваемой системе соотношений на слова вида s₂(x) .

Язык (множество слов S(X) ) задается грамматикой G(S) – структурой правил, которые позволяют порождать все слова 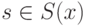$s\in S(x)$ и только их.

Грамматический анализ – процесс редукции к нетерминальному символу или слову.

Множество 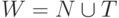$W = N\cup T$ – словарь грамматики G. Правила вывода – это непустое множество правил вида $f\to g$ , где $f, g\in W$ , а " $\to$ " – отношение вида "левое (можно) заменить на правое".

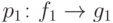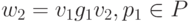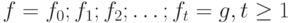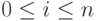Слово $w_1\in W$ выводимо из слова $w_2\in W$ с помощью правила $p_1\colon f_1\to g_1$ , если $w_1=v_{1}f_{1}v_{2}$ , $w_{2}=v_{1}g_{1}v_{2}, p_{1}\in P$ . Последовательность $f = f_{0}; f_{1}; f_{2}; \ldots; f_t = g, t \ge 1$ называется выводом g из f, если f_i+1 выводимо из f_i для всех $0\le i\le n$ . Признаком завершения процесса (последовательности) вывода является отсутствие слова, выводимого из g.

Пример. Опишем элементы естественного, например, русского языка в терминах формальных грамматик. Алфавит языка X = {А, а, Б, б, ... , Я, я, ., ,, :, ;, ., !, ?, ", ", (, )}, T={<корни>, <приставки> и т.д.}, N = {предложение, подлежащее, сказуемое, глагол, местоимение и т.д.}, n₀ = "предложение" . Например, пусть

Т = {арбуз, банан, красный, греет, загорает, бок},

N = {сказуемое, подлежащее, определение, дополнение, группа подлежащего, группа сказуемого},

n₀ = {предложение} ,

P = {p₁: предложение $\to$ (группа подлежащего), (группа сказуемого ),

p₂: группа подлежащего $\to$ (определение)(подлежащее) ,

p₃: группа сказуемого $\to$ (сказуемое) (дополнение) ,

p₄: определение $\to$ "красный" ,

p₅: подлежащее $\to$ "арбуз" ,

p₆: подлежащее $\to$ "банан" ,

p₇: сказуемое $\to$ "греет" ,

p₈: дополнение $\to$ "банан" ,

p₉: дополнение $\to$ "бок"} .

Тогда справедливы следующие выводы:

предложение (группа подлежащего)(группа сказуемого) $\to$

(определение) (подлежащее) (группа сказуемого) $\to$

(определение) (подлежащее) (сказуемое) (дополнение) $\to$

"красный" (подлежащее) (сказуемое )(дополнение) $\to$

"красный арбуз" (сказуемое) (дополнение) $\to$

"красный арбуз греет" (дополнение) $\to$

"красный арбуз греет бок".

Таким образом, мы по формальным правилам построили предложение естественного языка.

Различают четыре основных типа формальных грамматик.

Грамматика типа 0 (G–0) – грамматика, в которой нет ограничений на правила вывода (то есть в правиле вывода $f\to g$ , f и g – любые).

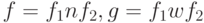Грамматика типа 1 (G–1) – грамматика, в которой содержатся правила $f\to g$ вида $f = f_{1}nf_{2}, g=f_{1}wf_{2}$ , где n – нетерминальный символ 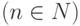$(n\in N)$ , f₁ , f₂ , w – цепочки из словаря W.

Грамматика типа 2 (G–2) – грамматика, в которой допустимы лишь правила вида 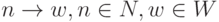$n\to w, n\in N, w\in W$ .

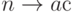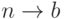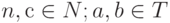Грамматика типа 3 (G–3) имеет правила вида $n\to aс$ , либо $n\to b$ , где $n, с\in N; a, b\in T$ .

Грамматики типа G–0 называются свободными, типа G–1 – контекстно-зависимыми, типа G–2 – контекстно-свободными, типа G–3 – регулярными или автоматными.

Дальше >>

Введение в информатику

Формальные языки и грамматики

Вопросы и ответы

Студенты

Авторизоваться

Введение в информатику

Формальные языки и грамматики

Вопросы и ответы

Студенты