| Почему сейчас я не зачислена на курс? |
Статистический анализ числовых величин
8.6. Проверка гипотезы симметрии
Рассмотрим методы проверки гипотезы симметрии функции распределения относительно 0. Сначала обсудим, какого типа отклонения от гипотезы симметрии можно ожидать при альтернативных гипотезах?
Как и в случае проверки однородности независимых выборок, в зависимости от вида альтернативной гипотезы выделяют два подуровня моделей. Рассмотрим сначала альтернативу сдвига
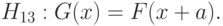
В этом случае распределение  при альтернативе отличается сдвигом от симметричного относительно 0. Для проверки гипотезы однородности может быть использован критерий знаковых рангов, разработанный Вилкоксоном (см., например, справочник [
[
8.11
]
, с.46-53]).
при альтернативе отличается сдвигом от симметричного относительно 0. Для проверки гипотезы однородности может быть использован критерий знаковых рангов, разработанный Вилкоксоном (см., например, справочник [
[
8.11
]
, с.46-53]).
Он строится следующим образом. Пусть  является рангом
является рангом 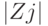 в ранжировке от меньшего к большему абсолютных значений разностей
в ранжировке от меньшего к большему абсолютных значений разностей  . Положим для
. Положим для 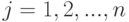
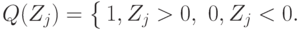
Статистика критерия знаковых рангов имеет вид

Таким образом, нужно просуммировать ранги положительных разностей в вариационном ряду, построенном стандартным образом по абсолютным величинам всех разностей.
Для практического использования статистики критерия знаковых рангов Вилкоксона либо обращаются к соответствующим таблицам и программному обеспечению, либо применяют асимптотические соотношения. При выполнении нулевой гипотезы статистика
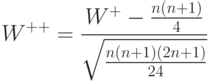
 ) стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1. Следовательно, правило принятия решений на уровне значимости 5% имеет обычный вид: если
) стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1. Следовательно, правило принятия решений на уровне значимости 5% имеет обычный вид: если
Альтернативная гипотеза общего вида записывается как

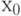 . Таким образом, проверке подлежит гипотеза симметрии относительно 0, которую можно переписать в виде
. Таким образом, проверке подлежит гипотеза симметрии относительно 0, которую можно переписать в виде
Для построенной по выборке 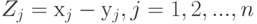 , эмпирической функции распределения
, эмпирической функции распределения  последнее соотношение выполнено лишь приближенно:
последнее соотношение выполнено лишь приближенно:
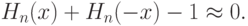
Как измерять отличие от 0? По тем же соображениям, что и в предыдущем параграфе, целесообразно использовать статистику типа омега-квадрат. Соответствующий критерий был предложен в работе [ [ 8.3 ] ]. Он имеет вид \omega_n^2=\sum_{j=1}^n(H_n(Z_j)+H_n(-Z_j)-1)^2
В работе [ [ 8.7 ] ] найдено предельное распределение этой статистики:
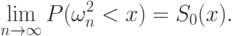
В табл.8.2 приведены критические значения статистики типа омега-квадрат для проверки симметрии распределения (и тем самым для проверки однородности связанных выборок), соответствующие наиболее распространенным значениям уровней значимости (расчеты проведены Г.В. Мартыновым). При практических вычислениях удобнее принять, что эмпирическая функция распределения  - это доля результатов наблюдений, не превосходящих
- это доля результатов наблюдений, не превосходящих  .
.
Как следует из табл.8.2, правило принятия решений при проверке однородности связанных выборок в наиболее общей постановке и при уровне значимости 5% формулируется следующим образом: вычислить статистику 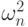 . Если
. Если  , то принять гипотезу однородности. В противном случае - отвергнуть.
, то принять гипотезу однородности. В противном случае - отвергнуть.
Значение функции распределения  |
Уровень значимости  |
Критическое значение х статистики 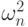 |
|---|---|---|
| 0,90 | 0,10 | 1,20 |
| 0,95 | 0,05 | 1,66 |
| 0,99 | 0,01 | 2,80 |
Пример. Пусть величины  , таковы:
, таковы:
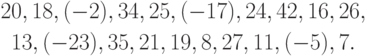
Соответствующий вариационный ряд  имеет вид:
имеет вид:
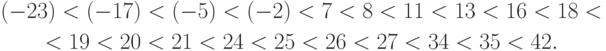
Для расчета значения статистики 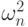 построим табл.8.3 из 7 столбцов и 20 строк, не считая заголовков столбцов (сказуемого таблицы). В первом столбце указаны номера (ранги) членов вариационного ряда, во втором - сами эти члены, в третьем - значения эмпирической функции распределения при значениях аргумента, совпадающих с членами вариационного ряда. В следующем столбце приведены члены вариационного ряда с обратным знаком, а затем указываются соответствующие значения эмпирической функции распределения. Например, поскольку минимальное наблюдаемое значение равно (-23), то
построим табл.8.3 из 7 столбцов и 20 строк, не считая заголовков столбцов (сказуемого таблицы). В первом столбце указаны номера (ранги) членов вариационного ряда, во втором - сами эти члены, в третьем - значения эмпирической функции распределения при значениях аргумента, совпадающих с членами вариационного ряда. В следующем столбце приведены члены вариационного ряда с обратным знаком, а затем указываются соответствующие значения эмпирической функции распределения. Например, поскольку минимальное наблюдаемое значение равно (-23), то 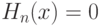 при
при  , а потому для членов вариационного ряда с 14-го по 20-й в пятом столбце стоит 0. В качестве другого примера рассмотрим минимальный член вариационного ряда, т.е. (-23). Меняя знак, получаем 23. Это число стоит между 13-м и 14-м членами вариационного ряда, 21<23<24.
На этом интервале эмпирическая функция распределения совпадает со своим значением в левом конце, поэтому следует записать в пятом столбце значение 0,65. Остальные ячейки пятого столбца заполняются аналогично. На основе третьего и пятого столбцов элементарно заполняется шестой столбец, а затем и седьмой. Остается найти сумму значений, стоящих в седьмом столбце. Подобная таблица удобна как для ручного счета, так и при использовании электронных таблиц типа Excel.
, а потому для членов вариационного ряда с 14-го по 20-й в пятом столбце стоит 0. В качестве другого примера рассмотрим минимальный член вариационного ряда, т.е. (-23). Меняя знак, получаем 23. Это число стоит между 13-м и 14-м членами вариационного ряда, 21<23<24.
На этом интервале эмпирическая функция распределения совпадает со своим значением в левом конце, поэтому следует записать в пятом столбце значение 0,65. Остальные ячейки пятого столбца заполняются аналогично. На основе третьего и пятого столбцов элементарно заполняется шестой столбец, а затем и седьмой. Остается найти сумму значений, стоящих в седьмом столбце. Подобная таблица удобна как для ручного счета, так и при использовании электронных таблиц типа Excel.
 |
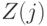 |
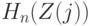 |
 |
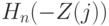 |
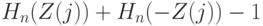 |
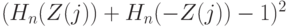 |
|---|---|---|---|---|---|---|
| 1 | -23 | 0,05 | 23 | 0,65 | -0,30 | 0,09 |
| 2 | -17 | 0,10 | 17 | 0,45 | -0,45 | 0,2025 |
| 3 | -5 | 0,15 | 5 | 0,20 | -0,65 | 0,4225 |
| 4 | -2 | 0,20 | 2 | 0,20 | -0,60 | 0,36 |
| 5 | 7 | 0,25 | -7 | 0,10 | -0,65 | 0,4225 |
| 6 | 8 | 0,30 | -8 | 0,10 | -0,60 | 0,36 |
| 7 | 11 | 0,35 | -11 | 0,10 | -0,55 | 0,3025 |
| 8 | 13 | 0,40 | -13 | 0,10 | -0,50 | 0,25 |
| 9 | 16 | 0,45 | -16 | 0,10 | -0,45 | 0,2025 |
| 10 | 18 | 0,50 | -18 | 0,05 | -0,45 | 0,2025 |
| 11 | 19 | 0,55 | -19 | 0,05 | -0,40 | 0,16 |
| 12 | 20 | 0,60 | -20 | 0,05 | -0,35 | 0,1225 |
| 13 | 21 | 0,65 | -21 | 0,05 | -0,30 | 0,09 |
| 14 | 24 | 0,70 | -24 | 0 | -0,30 | 0,09 |
| 15 | 25 | 0,75 | -25 | 0 | -0,25 | 0,0625 |
| 16 | 26 | 0,80 | -26 | 0 | -0,20 | 0,04 |
| 17 | 27 | 0,85 | -27 | 0 | -0,15 | 0,0225 |
| 18 | 34 | 0,90 | -34 | 0 | -0,10 | 0,01 |
| 19 | 35 | 0,95 | -35 | 0 | -0,05 | 0,0025 |
| 20 | 42 | 1,00 | -42 | 0 | 0 | 0 |
Результаты расчетов (суммирование значений по седьмому столбцу табл.8.3) показывают, что значение статистики 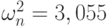 . В соответствии с табл.8.2 это означает, что на любом используемом в прикладных эконометрических исследованиях уровнях значимости отклоняется гипотеза симметрии распределения относительно 0 (а потому и гипотеза однородности в связанных выборках).
. В соответствии с табл.8.2 это означает, что на любом используемом в прикладных эконометрических исследованиях уровнях значимости отклоняется гипотеза симметрии распределения относительно 0 (а потому и гипотеза однородности в связанных выборках).
В настоящей лекции затронута лишь небольшая часть непараметрических методов анализа числовых статистических данных. В частности, обратим внимание на непараметрические оценки плотности, которые используются для описания данных, проверки однородности, в задачах восстановления зависимостей и других областях прикладной статистики. Непараметрические оценки плотности рассмотрены в "Описание данных" .
