Статистический анализ числовых величин

8.5. Методы проверки однородности связанных выборок

Начнем с практического примера. Приведем письмо главного инженера подмосковного химического комбината (некоторые названия изменены).

Комментарий. Вязкость - один из показателей качества мастики. Измерять его можно с помощью различных способов, которые, как оказалось, дают разные результаты. Ничего необычного в этом нет. Однако поставщику и потребителю следует согласовать способы измерения показателей качества. Иначе достаточно часто поставщик (производитель) будет утверждать, что он выполнил условия контракта, а потребитель заявлять, что нет. Такая конфликтная ситуация иногда называется арбитражной, поскольку для ее решения стороны могут обращаться в арбитражный суд. Простейший метод согласования способов измерения показателей состоит в том, чтобы выбрать один из них и внести в государственный стандарт, который тем самым будет содержать не только описание продукции, перечень ее показателей качества и требований к ним, но и способы измерения этих показателей.

Заключение по статистическим данным, представленным химическим комбинатом. Для каждой из 213 партий мастики представлены два числа - результат измерения вязкости на нестандартном приборе фабрики им. Петрова и результат измерения вязкости на стандартном вискозиметре ВЗ-4. Требуется установить, дают ли два указанных метода сходные результаты. Если они дают сходные результаты, то нет необходимости вводить в соответствующий ГОСТ указание о методе определения вязкости. Если же методы дают существенно различные результаты, то подобное указание ввести необходимо.

Для применения статистических методов в рассматриваемой задаче необходимо описать вероятностную модель. Считаем, что статистические данные имеют вид 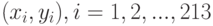где - результат измерения на нестандартном приборе фабрики им. Петрова в -ой партии, а - результат измерения вязкости на стандартном вискозиметре ВЗ-4 в той же -ой партии. Пусть - истинное значение показателя качества в -ой партии. Естественно считать, что указанные выше случайные векторы независимы в совокупности. При этом они не являются одинаково распределенными, поскольку отличаются истинными значениями показателей качества . Принимаем, что при каждом случайные величины и независимы и одинаково распределены. Это условие и означает однородность в связанных выборках. Параметры связи - величины . Их наличие не позволяет объединить первые координаты в одну выборку, вторую - во вторую, как делалось в случае проверки однородности двух независимых выборок.

В предположении непрерывности функций распределения из условия однородности в связанных выборках вытекает, что

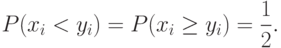
Рассмотрим случайные величины 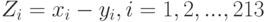. Из последнего соотношения вытекает, что при справедливости гипотезы однородности для связанных выборок эти случайные величины имеют нулевые медианы. Другими словами, проверка того, что методы измерения вязкости дают схожие результаты, эквивалентна проверке равенства 0 медиан величин .

Для проверки гипотезы о том, что медианы величин нулевые, применим широко известный критерий знаков (см., например, справочник [ [ 2.1 ] , с.89-91]). Согласно этому критерию необходимо подсчитать, в скольких партиях 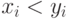и в скольких 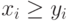. Для представленных химическим комбинатом данных 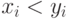в 187 случаях из 213 и 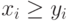в 26 случаях из 213.

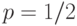Если рассматриваемая гипотеза верна, то число осуществлений события имеет биномиальное распределение с параметрами и 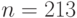. Математическое ожидание 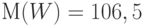, а среднее квадратическое отклонение 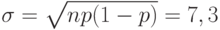. Следовательно, интервал 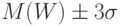- это интервал 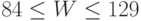. Найденное по данным химического комбината значение лежит далеко вне этого интервала. Поэтому рассматриваемую гипотезу необходимо отвергнуть (на любом используемом в прикладных работах уровне значимости, в частности, на уровне значимости 1%).

Таким образом, статистический анализ показывает, что два метода дают существенно различные результаты - по прибору фабрики им. Петрова результаты измерений, как правило, меньше, чем по вискозиметру ВЗ-4. Это означает, что в соответствующий ГОСТ целесообразно ввести указание на метод определения вязкости.

Система вероятностных моделей при проверке гипотезы однородности для связанных выборок. Как и в случае проверки однородности для независимых выборок, система вероятностных моделей состоит из трех уровней. Наиболее простая модель - на уровне однородности альтернативного признака - уже рассмотрена. Она сводится к проверке гипотезы о значении параметра биномиального распределения:

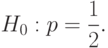
Речь идет о "критерии знаков". При справедливости гипотезы однородности число осуществлений события имеет биномиальное распределение с вероятностью успеха 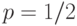и числом испытаний . Альтернативная гипотеза состоит в том, что вероятность успеха отличается от 1/2:

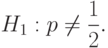
Гипотезу 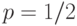можно проверять как непосредственно с помощью биномиального распределения (используя таблицы или программное обеспечение), так и опираясь на теорему Муавра-Лапласа. Согласно этой теореме

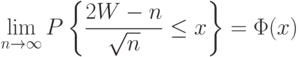
при всех , где - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Из теоремы Муавра-Лапласа вытекает правило принятия решений на уровне значимости 5%: если то гипотезу однородности связанных выборок принимают, в противном случае - отклоняют. Как обычно, при желании использовать другой уровень значимости применяют в качестве критического значения иной квантиль нормального распределения. Использование предельных теорем допустимо при достаточно больших объемах выборки. По поводу придания точного смысла термину "достаточно большой" продолжаются дискуссии. Обычно считается, что несколько десятков (два-три десятка) - это уже "достаточно много". Более правильно сказать, что ответ зависит от задачи, от ее сложности и практической значимости.

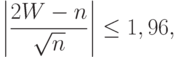
Второй уровень моделей проверки однородности связанных выборок - это уровень проверки однородности характеристик, прежде всего однородности математических ожиданий. Исходные данные - количественные результаты измерений (наблюдений, испытаний, анализов, опытов) двух признаков и 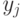, , 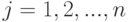а непосредственно анализируются их разности . Предполагается, что эти разности независимы в совокупности и одинаково распределены, однако функция распределения неизвестна статистику. Необходимо проверить непараметрическую гипотезу

Альтернативная гипотеза также является непараметрической и имеет вид:

Как и в случае проверки гипотезы однородности для независимых выборок с помощью критерия Крамера-Уэлча, в рассматриваемой ситуации естественно использовать статистику

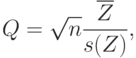
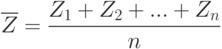
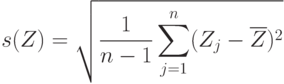
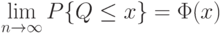
где среднее арифметическое разностей, а выборочное среднее квадратическое отклонение. Из Центральной предельной теоремы теории вероятностей и теорем о наследовании сходимости, полученных в монографии [ [ 1.15 ] ] и описанных в "Теоретическая база прикладной статистики" , вытекает, что при справедливости нулевой гипотезы при всех , где - функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1. Отсюда вытекает правило принятия решений на уровне значимости 5%: если то гипотезу однородности математических ожиданий связанных выборок принимают, в противном случае - отклоняют. Как обычно, при желании использовать другой уровень значимости применяют в качестве критического значения иной квантиль нормального распределения. Повторим, что использование предельных теорем допустимо при достаточно больших объемах выборки.

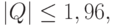
Третий уровень моделей проверки однородности связанных выборок - это уровень проверки однородности (совпадения) функций распределения. Необходимо проверить непараметрическую гипотезу наиболее всеохватного вида:

где

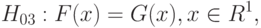
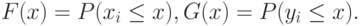
При этом предполагается, что все участвующие в вероятностной модели случайные величины независимы (в совокупности) между собой.

Отметим одно важное свойство функции распределения случайной величины . Если случайные величины и независимы и одинаково распределены, то для функции распределения 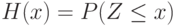случайной величины 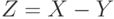выполнено, как нетрудно видеть, соотношение

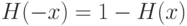
Это соотношение означает симметрию функции распределения относительно 0. Плотность такой функции распределения является четной функцией, ее значения в точках и 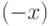совпадают.

Проверка гипотезы однородности связанных выборок в наиболее общем случае сводится к проверке симметрии функции распределения разности 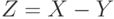относительно 0.