| Почему сейчас я не зачислена на курс? |
Выборочные исследования
Термин "выборочные исследования" применяют, когда невозможно изучить все единицы представляющей интерес совокупности. Приходится знакомиться с частью совокупности - с выборкой, а затем с помощью статистических методов и моделей переносить выводы с выборки на всю совокупность. Выборочные исследования - способ получения статистических данных и важная часть прикладной статистики. В качестве примера рассмотрим выборочные исследования предпочтений потребителей, которые часто проводят специалисты по маркетингу.
3.1. Применение случайной выборки (на примере оценивания функции спроса)
Функция спроса часто встречается в учебниках по экономической теории, но при этом обычно не рассказывается, как она получена. Между тем оценить ее по эмпирическим данным не так уж трудно. Например, можно выяснять ожидаемый спрос с помощью следующего простого приема - спрашиваем у потенциальных потребителей: "Какую максимальную цену Вы заплатили бы за такой-то товар?" Пусть для определенности речь идет о конкретном учебном пособии по менеджменту. В одном из экспериментов выборка состояла из 20 опрошенных. Они назвали следующие максимально допустимые для них цены (в рублях по состоянию на сентябрь 1998 г.):
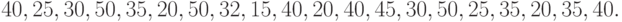
Первым делом названные величины надо упорядочить в порядке возрастания. Результаты представлены в табл.3.1. В первом столбце - номера различных численных значений (в порядке возрастания), названных потребителями. Во втором столбце приведены сами значения цены, названные ими. В третьем столбце указано, сколько раз названо то или иное значение.
№ п/п (  ) ) |
Цена 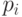 |
Повторы  |
Спрос 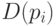 |
Прибыль  |
Прибыль  |
Прибыль 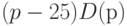 |
|---|---|---|---|---|---|---|
| 1 | 15 | 1 | 20 | 100 | 0 | - |
| 2 | 20 | 3 | 19 | 190 | 95 | - |
| 3 | 25 | 2 | 16 | 240 | 160 | 0 |
| 4 | 30 | 2 | 14 | 280 | 210 | 70 |
| 5 | 32 | 1 | 12 | 264 | 204 | 84 |
| 6 | 35 | 3 | 11 | 275 | 220 | 110 |
| 7 | 40 | 4 | 8 | 240 | 200 | 120 |
| 8 | 45 | 1 | 4 | 140 | 120 | 80 |
| 9 | 50 | 3 | 3 | 120 | 105 | 75 |
Таким образом, 20 потребителей назвали 9 конкретных значений цены (максимально допустимых или приемлемых для них значений), каждое из значений, как видно из третьего столбца, названо от 1 до 4 раз. Теперь легко построить выборочную функцию спроса в зависимости от цены. Она будет представлена в четвертом столбце, который заполним снизу вверх. Спрос как функция от цены  обозначен
обозначен 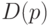 (от англ. Demand - спрос). Если мы будем предлагать товар по цене свыше 50 руб., то его не купит никто из опрошенных. При цене 50 руб. появляются 3 покупателя. Записываем 3 в четвертый столбец в девятую строку. А если цену понизить до 45? Тогда товар купят четверо - тот единственный, для кого максимально возможная цена - 45, и те трое, кто был согласен на более высокую цену - 50 руб.
Таким образом, легко заполнить столбец 4, действуя по правилу: значение в клетке четвертого столбца равно сумме значений в находящейся слева клетке третьего столбца и в лежащей снизу клетке четвертого столбца. Например, за 30 руб. купят товар 14 человек, а за 20 руб. - 19.
(от англ. Demand - спрос). Если мы будем предлагать товар по цене свыше 50 руб., то его не купит никто из опрошенных. При цене 50 руб. появляются 3 покупателя. Записываем 3 в четвертый столбец в девятую строку. А если цену понизить до 45? Тогда товар купят четверо - тот единственный, для кого максимально возможная цена - 45, и те трое, кто был согласен на более высокую цену - 50 руб.
Таким образом, легко заполнить столбец 4, действуя по правилу: значение в клетке четвертого столбца равно сумме значений в находящейся слева клетке третьего столбца и в лежащей снизу клетке четвертого столбца. Например, за 30 руб. купят товар 14 человек, а за 20 руб. - 19.
Зависимость спроса от цены - это зависимость четвертого столбца от второго. Табл.3.1 дает нам девять точек такой зависимости. Зависимость можно представить на рисунке, в координатах "спрос - цена" ( рис. 3.1). Если абсцисса - это спрос, а ордината - цена, то девять точек на кривой спроса, перечисленные в порядке возрастания абсциссы, имеют вид:

Эти девять точек можно использовать для построения кривой спроса каким-либо графическим или расчетным способом, например, методом наименьших квадратов (см.9.2).
Кривая спроса, в соответствии с экономической теорией, убывает, имея направления от левого верхнего угла чертежа к правому. Однако заметны отклонения от гладкого вида функции, связанные, в частности, с естественным пристрастием потребителей к круглым числам. Заметьте, все опрошенные, кроме одного, назвали числа, кратные 5 руб.
Данные табл.3.1 могут быть использованы для выбора цены продавцом-монополистом, или организацией, действующей на рынке монополистической конкуренции. Пусть расходы на изготовление или оптовую покупку единицы товара равны 10 руб. Например, оптовая цена книги - 10 руб. По какой цене ее продавать на том рынке, функцию спроса для которого мы только что нашли? Для ответа на этот вопрос вычислим суммарную ожидаемую прибыль, т.е. произведение прибыли на одном экземпляре  на число проданных (точнее, запрошенных) экземпляров
на число проданных (точнее, запрошенных) экземпляров 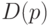 . Результаты приведены в пятом столбце табл.3.1. Максимальная прибыль, равная 280 руб., достигается при цене 30 руб. за экземпляр. При этом из 20 потенциальных покупателей окажутся в состоянии заплатить за книгу 14, т.е. 70%.
. Результаты приведены в пятом столбце табл.3.1. Максимальная прибыль, равная 280 руб., достигается при цене 30 руб. за экземпляр. При этом из 20 потенциальных покупателей окажутся в состоянии заплатить за книгу 14, т.е. 70%.
Если же удельные издержки производства, приходящиеся на одну книгу (или оптовая цена), повысятся до 15 руб., то данные столбца 6 табл.3.1 показывают, что максимальная прибыль, равная 220 руб. (она, разумеется, меньше, чем в предыдущем случае), достигается при более высокой цене - 35 руб. Эта цена доступна 11 потенциальным покупателям, т.е. 55% от всех возможных покупателей. При дальнейшем повышении издержек, скажем, до 25 руб., как вытекает из данных седьмого столбца табл.3.1, максимальная прибыль, равная 120 руб., достигается при цене 40 руб. за единицу товара, что доступно 8 лицам, т.е. 40% покупателей. Отметьте, что при повышении оптовой цены на 10 руб. оказалось выгодным увеличить розничную лишь на 5, поскольку более резкое повышение привело бы к такому сокращению спроса, которое перекрыло бы эффект от повышения удельной прибыли (т.е. прибыли, приходящейся на одну проданную книгу).
Представляет интерес анализ оптимального объема выпуска при различных значениях удельных издержек (табл.3.2).
В табл.3.2 звездочками указаны максимальные значения прибыли при том или ином значении издержек, не включенном в табл.3.1. Для удобства результаты расчетов оптимальных объемов выпуска и соответствующих цен из табл. 3.1 и 3.2 приведены в табл.3.3.
№ п/п (  ) ) |
Цена 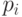 |
Спрос 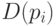 |
Прибыль 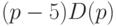 |
Прибыль  |
Прибыль  |
Прибыль 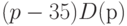 |
Прибыль 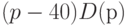 |
|---|---|---|---|---|---|---|---|
| 1 | 15 | 20 | 200 | - | - | - | - |
| 2 | 20 | 19 | 285 | 0 | - | - | - |
| 3 | 25 | 16 | 320 | 80 | - | - | - |
| 4 | 30 | 14 | 350* | 140 | 0 | - | - |
| 5 | 32 | 12 | 324 | 144 | 24 | - | - |
| 6 | 35 | 11 | 330 | 165* | 55 | 0 | - |
| 7 | 40 | 8 | 280 | 160 | 80* | 40 | 0 |
| 8 | 45 | 4 | 160 | 100 | 60 | 40 | 20 |
| 9 | 50 | 3 | 135 | 90 | 60 | 45* | 30* |
| Издержки | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 |
| Оптимальный выпуск | 14 | 14 | 11 | 11 | 8 | 8 | 3 | 3 |
| Цена | 30 | 30 | 35 | 35 | 40 | 40 | 50 | 50 |
Как видно из табл.3.3, с ростом издержек оптимальный выпуск падает, а цена растет. При этом изменение издержек на 5 единиц может вызывать, а может и не вызывать повышения цены. В этом проявляется микроструктура функции спроса - небольшое повышение цены может привести к тому, что значительные группы покупателей откажутся от покупок, и прибыль упадет.
Этот эффект напоминает известное в экономической теории разделение налогового бремени между производителем и потребителем. Неверно говорить, что производитель перекладывает издержки или, конкретно, налоги, на потребителя, повышая цену на их величину, поскольку при этом сокращается спрос (и выпуск), а потому и прибыль производителя.
Дальнейшее ясно - если оптовая цена будет повышаться, то и дающая максимальную прибыль розничная цена также будет повышаться, и все меньшая доля покупателей сможет приобрести товар. Крайняя точка - оптовая цена, равная 45 руб. Тогда только трое (15%) купят товар за 50 руб., а прибыль продавца составит только 15 руб. Наглядно видно, что повышение издержек производства приводит к ориентации производителя на наиболее богатые слои населения, но и повышение цен (до оптимального для монополиста-производителя уровня) не приводит к повышению прибыли, напротив, она снижается, и при этом большинство потенциальных потребителей не в состоянии купить товар. Таково влияние инфляции издержек на экономическую жизнь.
Отметим, что рыночные структуры не в состоянии обеспечить всех желающих - это просто не выгодно. Так, из 20 опрошенных лишь 14, т.е. 70%, могут рассчитывать на покупку, даже при минимальных издержках и ценах. Если общество желает чем-либо обеспечить всех граждан, оно должно раздавать это благо бесплатно, как это делается, например, с учебниками в школах.
Описанный выше метод оценивания спроса был разработан в Институте высоких статистических технологий и эконометрики в 1993 г.
Для изучения предпочтений потребителей часто используют более изощренные методы. Рассмотрим некоторые из них.

