| Стоимость "обучения" |
Прикладная теория организации очередей
Пример 13.6.1: Средние времена ожидания GI/M/1
Для 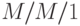 мы находим
мы находим  . Для
. Для  получается из уравнения:
получается из уравнения:
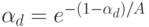
где 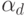 находится в пределах (0,1).
находится в пределах (0,1).
Можно показать, что 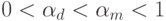 . Таким образом, система организации очереди D/M/1 будет всегда иметь среднее время ожидания меньше, чем
. Таким образом, система организации очереди D/M/1 будет всегда иметь среднее время ожидания меньше, чем 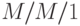 .
.
Для = 0,5 Эрл. мы находим следующие средние времена ожидания для всех клиентов (13.78):

где среднее время пребывания в системе используется как единица времени ( 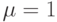 ).Среднее время ожидания пропорционально прошедшему до данного момента времени с коэффициентом формы распределения интервала поступления.
).Среднее время ожидания пропорционально прошедшему до данного момента времени с коэффициентом формы распределения интервала поступления.
Распределение времени ожидания: GI/M/1, FCFS
Когда клиент достигает системы организации очереди, число клиентов в системе геометрическое распределено и клиент, предположительно, ожидает некоторое время, равное нескольким геометрически экспоненциально распределенным фазам.
Это сводится к экспоненциально распределенному времени ожидания с параметром, данным в (13.80), когда дисциплина организации очереди - FCFS (секция 12.4 и рис.4.9).
Циклическое и совместное использование процессора
Циклическая ( RR - Round Robin ) модель организации очереди (рис.13.6) является моделью для исследования компьютерной системы с разделением времени, где мы хотим обеспечить быстрое время реакции для самых коротких работ. Эта дисциплина организации очереди также названа справедливой организацией очереди, потому что доступные ресурсы одинаково распределены среди заявок на работу (клиенты) в системе.
Задача распределена в интервале времени  для момента обслуживания. Если задача не закончена в этот интервал, то она возвращается в FCFS -очередь, где ставится на равных условиях с новыми задачами. Если мы допускаем уменьшение
для момента обслуживания. Если задача не закончена в этот интервал, то она возвращается в FCFS -очередь, где ставится на равных условиях с новыми задачами. Если мы допускаем уменьшение  , до нуля, то получаем дисциплину организации очереди типа "совместного использования процессора (PS - Processor Sharing).
, до нуля, то получаем дисциплину организации очереди типа "совместного использования процессора (PS - Processor Sharing).
Заявки на новые работы помещаются в FCFS -очередь, где они находятся на ожидании, пока не будут взяты на обслуживание, в пределах интервала времени (слота)  , который одинаков для всех заявок на работу. Если работа не закончена в пределах интервала времени, обслуживание прерывается и работа помещается в конце FCFS -очереди. Это продолжается, пока не будет представлено полное время обслуживания.
, который одинаков для всех заявок на работу. Если работа не закончена в пределах интервала времени, обслуживание прерывается и работа помещается в конце FCFS -очереди. Это продолжается, пока не будет представлено полное время обслуживания.
Мы принимаем, что очередь неограниченна и что заявки (новые работы) прибывают согласно Пуассоновскому процессу (  ). Распределение времени обслуживания может быть общим со средней величиной s. Интервал времени может изменяться.
). Распределение времени обслуживания может быть общим со средней величиной s. Интервал времени может изменяться.
Если он становится конечным, и все работы будут заканчиваться за один интервал, то мы получаем просто систему организации очереди 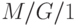 с дисциплиной FCFS. Если мы допускаем уменьшение интервала времени до нуля, то получаем дисциплину организации очереди типа "совместного использования процессора" (PS - Processor Sharing), которая имеет множество хороших аналитических свойств. Она была исследована Клейнроком (1967) и подробно изложена в (Kleinrock, 1976 [67] ). Модель совместного использования процессора может интерпретироваться как система организации очереди, где все работы обслуживаются непрерывно обслуживающим прибором (режим разделения времени). Если есть
с дисциплиной FCFS. Если мы допускаем уменьшение интервала времени до нуля, то получаем дисциплину организации очереди типа "совместного использования процессора" (PS - Processor Sharing), которая имеет множество хороших аналитических свойств. Она была исследована Клейнроком (1967) и подробно изложена в (Kleinrock, 1976 [67] ). Модель совместного использования процессора может интерпретироваться как система организации очереди, где все работы обслуживаются непрерывно обслуживающим прибором (режим разделения времени). Если есть  работ в системе, каждая из них получает
работ в системе, каждая из них получает  часть емкости компьютера. Так что нет никакой очереди, и дисциплина организации очереди бессмысленна.
часть емкости компьютера. Так что нет никакой очереди, и дисциплина организации очереди бессмысленна.
Когда предложенная нагрузка  меньше единицы, можно показать, что вероятности устойчивых состояний равны:
меньше единицы, можно показать, что вероятности устойчивых состояний равны:
 |
( 13.81) |
то есть, получается, геометрическое распределение со средней величиной 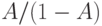 . Среднее время пребывания в системе (среднее время реакции) для работ с продолжительностью
. Среднее время пребывания в системе (среднее время реакции) для работ с продолжительностью  равно:
равно:
 |
( 13.82) |
Если бы эта работа была одна в системе, то ее время пребывания в системе было бы  . Так как нет очереди, мы можем говорить о средней задержке для работ с продолжительностью
. Так как нет очереди, мы можем говорить о средней задержке для работ с продолжительностью 
 |
( 13.83) |
Соответствующие средние величины для произвольной работы естественно равны:
 |
( 13.84) |
 |
( 13.85) |
Это показывает, что мы получаем точно такие же средние величины, что и для 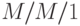 (секция 12.2.4). Но фактическое среднее время ожидания становится пропорциональным продолжительности работы. Такое свойство зачастую весьма желательно. Мы не предполагаем, что имеются какие-либо предварительные знания о продолжительности работы.
(секция 12.2.4). Но фактическое среднее время ожидания становится пропорциональным продолжительности работы. Такое свойство зачастую весьма желательно. Мы не предполагаем, что имеются какие-либо предварительные знания о продолжительности работы.
Среднее время ожидания пропорционально среднему времени обслуживания. Пропорциональность не должна пониматься при этом методе так, что две работы одной той же продолжительности имеют одинаковое время ожидания. Это справедливо только в среднем. По сравнению с результатами, которые мы получили ранее для 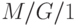 (формула Полячека-Хинчина (13.2)), результаты могут не соответствовать нашим интуитивным представлениям.
(формула Полячека-Хинчина (13.2)), результаты могут не соответствовать нашим интуитивным представлениям.
Очень полезное свойство модели совместно используемого процессора: процесс выхода из системы - Пуассоновский процесс, как и процесс поступления вызовов (секция 14.2). Это интуитивно объясняется тем фактом, что процесс выхода из системы получается из процесса поступления вызовов стохастическим смещением отдельных моментов поступления. Сдвиг по времени равен времени реакции со средней величиной, приведенной в (13.82) (секция 6.3.1, теорема Пальма).
Совместно использующая процессор модель очень полезна для того, чтобы анализировать системы с разделением времени, и для сетей, использующих организации очереди (Лекция 14).
Краткие итоги:
-
Для описания типа нагрузки и структуры очереди D.G. Kendall (1951 [61] ) ввел следующую систему обозначений для моделей организации очереди:
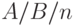
где
 - процесс поступления вызовов,
- процесс поступления вызовов, - распределение времени обслуживания,
- распределение времени обслуживания, - число обслуживающих приборов.
- число обслуживающих приборов. - Применяются три классических дисциплины организации очереди: FCFS (First Come - First Served): "Первый Пришел - Первый Обслужен", LCFS (Last Come - First Served) - "Последний Пришел - Первый Обслужен" и SIRO (Service In Random Orde) - "Обслуживание в Случайном Порядке".
-
Для компьютерных систем мы часто пробуем уменьшить полное время ожидания. Это может быть сделано с использованием дисциплин, учитывающих критерии времени обслуживания:
- Shortest Job First - "Первым - Самое короткое Задание";
- RR (Round Robin) - циклическая (круговая система);
- PS (Processor Sharing) - совместное использование процессора;
- FB (Foreground / Background) - "Передняя позиция план /Задняя позиция".
- На практике клиенты часто разделяются на N приоритетных классов. Различают два типа приоритетов: Неприоритетный, Приоритетный. Если обслуживаемый клиент имеет более низкий приоритет, чем новый поступивший вызовов, то обслуживание прерывается. При этом возможно возвращение к работе.
- Приоритетное возвращение к работе имеет варианты: приоритетное без повторения, приоритетное с повторением. В поведении клиентов рассматриваются дисциплины: Отказывающийся становиться в очередь, Нарушающий очередь, Перепрыгивающий.
-
Среднее время ожидания для системы
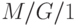 определяется формулой Полячека-Хинчина:
определяется формулой Полячека-Хинчина:
- Если мы рассматриваем только клиентов, которые задержаны, то можем найти моменты распределения времени ожидания для классических дисциплин организации очереди: FCFS, LCFS, M/G/1/k для системы, где общее количество мест ожидания для клиентов конечно и равно k.
- В соответствии с различными стратегиями организации очереди, времена ожидания могут быть распределены среди клиентов согласно приоритету. В этом случае клиенты разделены на
 классов (потоков нагрузки). В результате распределение времени обслуживания становится взвешенной суммой распределений времени обслуживания отдельных классов (секция 3.2: комбинация параллельных процессов).
классов (потоков нагрузки). В результате распределение времени обслуживания становится взвешенной суммой распределений времени обслуживания отдельных классов (секция 3.2: комбинация параллельных процессов). - Ранее мы предположили, что время обслуживания клиента не зависит от дисциплины организации очереди. Пропускная способность обслуживающего прибора, таким образом, постоянна и не зависит, например, от длины очереди. Дисциплина организации очереди, как говорят, сохраняет работу.
- Функция нагрузки
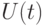 обозначает время, которое требуются, чтобы обслужить клиента, прибывшего в систему в момент времени
обозначает время, которое требуются, чтобы обслужить клиента, прибывшего в систему в момент времени  . В момент поступления вызова функция
. В момент поступления вызова функция 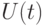 увеличивается скачком на величину времени обслуживания, а между поступлением вызовов
увеличивается скачком на величину времени обслуживания, а между поступлением вызовов 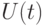 - уменьшается линейно с наклоном от 1 до 0.
- уменьшается линейно с наклоном от 1 до 0. - Используя принцип сохранения работы и функцию
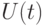 , можно получить закон сохранения Клейнрока: среднее время ожидания для всех классов взвешенной нагрузки не зависит от дисциплины очереди. Это справедливо только для неприоритетных дисциплин организации очереди.
, можно получить закон сохранения Клейнрока: среднее время ожидания для всех классов взвешенной нагрузки не зависит от дисциплины очереди. Это справедливо только для неприоритетных дисциплин организации очереди. -
Полное среднее время ожидания
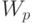 клиента класса
клиента класса  не зависит от того, какого класса клиенты ожидают, пока обработка очереди не будет закончена {V для всех классов одинаково}.
не зависит от того, какого класса клиенты ожидают, пока обработка очереди не будет закончена {V для всех классов одинаково}.
-
 приоритетная дисциплина организации очереди без прерывания обслуживания имеет среднее время ожидания
приоритетная дисциплина организации очереди без прерывания обслуживания имеет среднее время ожидания 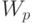 для класса
для класса  :
: .
. -
 дисциплина организации очереди с приоритетным возвращением к работе имеет среднее время ожидания
дисциплина организации очереди с приоритетным возвращением к работе имеет среднее время ожидания 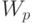 для класса
для класса  :
: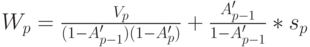 .
. - Для
 случай приоритетного возвращения к работе анализируется более сложно. Все клиенты должны иметь одинаковое среднее время обслуживания. Сначала среднее время ожидания может быть получено рассмотрением каждого класса автономно (12.15). Затем можно рассмотреть два класса вместе и получить время ожидания для двух классов и т. д.
случай приоритетного возвращения к работе анализируется более сложно. Все клиенты должны иметь одинаковое среднее время обслуживания. Сначала среднее время ожидания может быть получено рассмотрением каждого класса автономно (12.15). Затем можно рассмотреть два класса вместе и получить время ожидания для двух классов и т. д. - Системы с постоянными временами обслуживания имеют определяющее свойство: клиенты покидают обслуживающие приборы в том же самом порядке, в котором они приняты для обслуживания.
-
 обозначает среднее время ожидания для всех клиентов, и
обозначает среднее время ожидания для всех клиентов, и  обозначает среднее время ожидания для клиентов, которые стоят в очереди. Постоянные времена занятия требуют, чтобы мы помнили точное время начала. С экспоненциальным распределением иметь дело проще из-за отсутствия у него памяти: остающееся время "жизни" имеет то же самое распределение, как полное время "жизни" (секция 4.1), и поэтому мы можем забыть о периоде или моменте времени, когда начинается время обслуживания.
обозначает среднее время ожидания для клиентов, которые стоят в очереди. Постоянные времена занятия требуют, чтобы мы помнили точное время начала. С экспоненциальным распределением иметь дело проще из-за отсутствия у него памяти: остающееся время "жизни" имеет то же самое распределение, как полное время "жизни" (секция 4.1), и поэтому мы можем забыть о периоде или моменте времени, когда начинается время обслуживания. -
 - среднее время ожидания для всех клиентов, и
- среднее время ожидания для всех клиентов, и  - среднее время ожидания для клиентов, которые стоят в очереди в системе
- среднее время ожидания для клиентов, которые стоят в очереди в системе 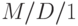 , определяются следующими формулами:
, определяются следующими формулами: .
. -
Для распределения времени ожидания
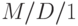 , FCFS формула времени ожидания имеет вид:
, FCFS формула времени ожидания имеет вид: ,
, -
Распределение времени ожидания
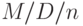 , FCFS определяется распределением Кроммелина:
, FCFS определяется распределением Кроммелина: ,
, - Системы
 эквивалентны относительно распределения времени ожидания.
эквивалентны относительно распределения времени ожидания. - Для конечной системы очереди
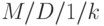 уравнения равновесия для вероятностей состояния
уравнения равновесия для вероятностей состояния  ,могут быть установлены с помощью уравнений состояний Фрея. Первые
,могут быть установлены с помощью уравнений состояний Фрея. Первые  уравнения (13.41) вместе с требованием нормализации и фактом, что предложенная нагрузка равняется обслуженной нагрузке плюс отклоненная нагрузка ( свойство PASTA ) дают в результате
уравнения (13.41) вместе с требованием нормализации и фактом, что предложенная нагрузка равняется обслуженной нагрузке плюс отклоненная нагрузка ( свойство PASTA ) дают в результате 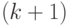 независимых линейных уравнений, которые легко решить.
независимых линейных уравнений, которые легко решить.

