| Стоимость "обучения" |
Теория вероятностей и статистика
Функции распределения
Временной интервал может быть описан случайной переменной Т, которая может быть охарактеризована функцией распределения F(t):
 |
( 3.1) |
В (3.1) мы интегрируем от 0, чтобы устранить возможную неоднозначность при  . При рассмотрении системы с ожиданием часто имеется положительная вероятность, что время ожидания равно нулю, a
. При рассмотрении системы с ожиданием часто имеется положительная вероятность, что время ожидания равно нулю, a  . С другой стороны, когда мы смотрим на времена между двумя моментами поступления вызова, мы обычно принимаем
. С другой стороны, когда мы смотрим на времена между двумя моментами поступления вызова, мы обычно принимаем 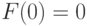 (Раздел. 5.2.3).
(Раздел. 5.2.3).
Вероятность того, что продолжительность временного интервала Т меньше или равна t
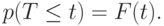
Иногда проще рассматривать дополнение функции распределения:
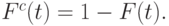
Ее также называют функцией распределения долговечности. Мы часто предполагаем, что 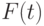 является дифференцируемой и что существует следующая функция плотности
является дифференцируемой и что существует следующая функция плотности  :
:
 |
( 3.2) |
Обычно мы принимаем, что время обслуживания является независимым от времени момента поступления вызова, и от времени обслуживания других вызовов. Аналитически, для любого распределения времени могут быть проведены множество вычислений. Вообще, мы всегда принимаем, что существует средняя величина времени обслуживания.
Характеристика распределений
Распределения времени, которые принимают только положительные значения, обладают некоторыми выгодными свойствами.
Для i-того нецентрального момента (см. Глоссарий), который мы обычно называем i -й момент, они могут быть показаны с помощью тождества Пальма:
 |
( 3.3) |
Тождество Пальма (3.3), которое справедливо для распределений времени "жизни" (определенно только для неотрицательных величин), было сначала доказано Пальма (1943, [79]) следующим образом.
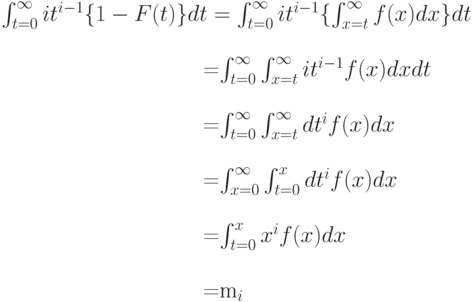
Порядок интегрирования может быть изменен, потому что подынтегральное выражение неотрицательно. Таким образом, мы доказали (3.3). Следующее упрощенное доказательство справедливо в предположении, что моменты существуют:
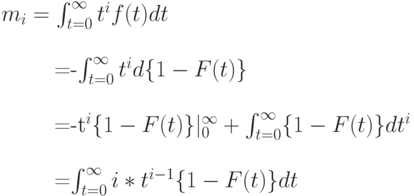
что и требовалось доказать.
Особо мы отмечаем два первых момента (если они существуют):
 |
( 3.4) |
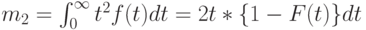 |
( 3.5) |
Средняя величина (математическое ожидание) - это первый момент.
 |
( 3.6) |
i -тый центральный момент определяется как:
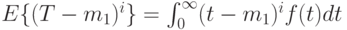 |
( 3.7) |
Дисперсия - 2-ой центральный момент:
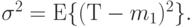
Просто показать, что
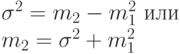 |
( 3.8) |
Распределение обычно однозначно определяется всеми его моментами. Нормализованная мера для отклонения распределения от средней величины - коэффициент вариации. Он определяется как отношение между стандартным отклонением и средней величиной:
 |
( 3.9) |
Эта величина безразмерна, и мы позже применим это свойство, чтобы характеризовать дискретные распределения (вероятности состояния). Другая мера нерегулярности - коэффициент формы Пальма, который определяется следующим образом:
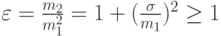 |
( 3.10) |
Коэффициент формы  , так же как
, так же как  независим от выбора масштаба времени, и в дальнейшем они еще появятся во многих формулах.
независим от выбора масштаба времени, и в дальнейшем они еще появятся во многих формулах.
Чем больше коэффициент формы, тем более нерегулярно распределение времени и, например, тем больше будет среднее время ожидания в системе с ожиданием. Коэффициент формы принимает минимальное значение, и равен единице для постоянных временных интервалов ( 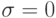 ).
).
Чтобы оценить распределение, вытекающие из наблюдений, мы часто удовлетворяемся знанием первых двух моментов (  и
и  или
или  ). Моменты более высокого порядка требуют получения чрезвычайно большого объема достоверных наблюдений. Распределения времени могут также быть характеризованы другими способами. Некоторые мы рассматриваем ниже.
). Моменты более высокого порядка требуют получения чрезвычайно большого объема достоверных наблюдений. Распределения времени могут также быть характеризованы другими способами. Некоторые мы рассматриваем ниже.
Пример3.1.1: Экспоненциальное распределение
Для экспоненциального распределения мы имеем:
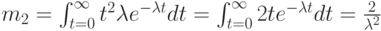
Заметим с удивлением, что эти два интеграла идентичны. Эти два подынтегральных выражения могут, кроме того, быть преобразованы к формулам Эрланга-3 и, соответственно, Эрланга-2 (4.8), функция плотности, которых имеет вероятность, равную единице:
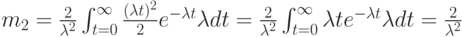
Пример 3.1.2: Постоянный временной интервал
Для постоянного временного интервала продолжительностью h мы имеем:

Остаток времени "жизни"
Мы хотим найти распределение времени остатка "жизни", при условии, что достигнут уже некоторый возраст  . Условное распределение
. Условное распределение 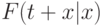 определено следующим образом, принимая
определено следующим образом, принимая 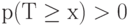 и
и
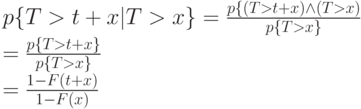
И, таким образом:
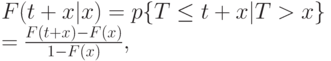 |
( 3.11) |
 |
( 3.12) |
Pис.3.1 иллюстрирует эти вычисления графически.
Средняя величина 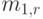 остаточного времени "жизни" может быть представлена как (3.4):
остаточного времени "жизни" может быть представлена как (3.4):
 |
( 3.13) |
Показатель время "гибели" х, то есть вероятность, что рассматриваемое время "жизни" заканчивается в пределах интервала  , при условии, что возраст* был достигнут, получается из (3.11), позволяя определить
, при условии, что возраст* был достигнут, получается из (3.11), позволяя определить  :
:
 |
( 3.14) |
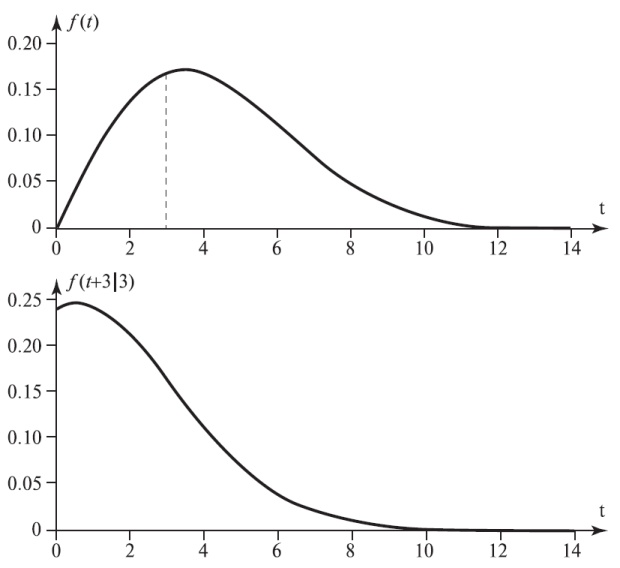
Рис. 3.1. Функия плотности остаточного времени "жизни", обусловленной данным возрастом х (3.11). Пример основан на распределении Вейбулла We (2,5), где х = 3 и F(3) = 0,3023
Условная функция плотности  также называется функцией интенсивности отказов. Если приводится эта функция, то
также называется функцией интенсивности отказов. Если приводится эта функция, то  может быть получена как решение следующего дифференциального уравнения:
может быть получена как решение следующего дифференциального уравнения:
 |
( 3.15) |
которое имеет следующее решение (предполагая, что 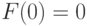 ):
):
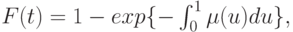 |
( 3.16) |
 |
( 3.17) |
Показатель "гибели"  является постоянным тогда и только, если время "жизни" имеет экспоненциальное распределение (часть 4).
является постоянным тогда и только, если время "жизни" имеет экспоненциальное распределение (часть 4).
Это фундаментальная характеристика показательного (экспоненциального) распределения, её называют Марковским свойством или свойством без последействия (при отсутствии памяти (возраста)): вероятность завершения не зависит от фактического возраста (истории) (секция 4.1).
Можно было бы ожидать, что среднее остаточное время "жизни" 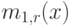 уменьшится при увеличении х, поскольку ожидаемое остаточное время жизни уменьшается, когда возраст х увеличивается. Но это верно не для всех случаев. Для показательного распределения с коэффициентом формы
уменьшится при увеличении х, поскольку ожидаемое остаточное время жизни уменьшается, когда возраст х увеличивается. Но это верно не для всех случаев. Для показательного распределения с коэффициентом формы  (секция 5.1) мы имеем
(секция 5.1) мы имеем 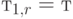 . Для распределений перевала
. Для распределений перевала  мы имеем
мы имеем 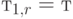 . (Секция . 4.2), тогда как для плоских распределений
. (Секция . 4.2), тогда как для плоских распределений 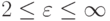 верно
верно  (Секция. 4.3).
(Секция. 4.3).
Пример3.1.3: распределение времени ожидания
Рассмотрим систему организации очереди с бесконечной очередью, где любой клиент не может быть заблокирован. Распределение времени ожидания 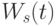 для случайного клиента обычно имеет положительную вероятность при
для случайного клиента обычно имеет положительную вероятность при  , потому что некоторые из клиентов обслуживаются немедленно без какой-либо задержки. Мы, таким образом, имеем
, потому что некоторые из клиентов обслуживаются немедленно без какой-либо задержки. Мы, таким образом, имеем  . Распределение времени ожидания
. Распределение времени ожидания  для клиентов, имеющих положительные времена ожидания, тогда определяется согласно уравнению (3.11):
для клиентов, имеющих положительные времена ожидания, тогда определяется согласно уравнению (3.11):
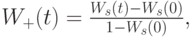
или, если мы обозначаем вероятность положительного времени ожидания 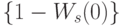 буквой
буквой  (вероятность задержки), то:
(вероятность задержки), то:
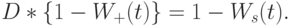 |
( 3.18) |
Тогда для функции плотности мы имеем согласно (3.11):
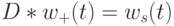 |
( 3.19) |
Средняя величина распределения получается:
 |
( 3.20) |
Где средняя величина для всех клиентов обозначена  , и средняя величина для задержанных клиентов обозначена
, и средняя величина для задержанных клиентов обозначена  . Формула действительна для любой системы с бесконечной очередью.
. Формула действительна для любой системы с бесконечной очередью.
Нагрузка по времени пребывания в системе продолжительностью меньше, чем х
До сих пор мы не рассматривали важности времени "жизни" заявок от их продолжительности. Важность времени "жизни" часто пропорциональна его продолжительности, например, когда мы рассматриваем нагрузку системы с организацией очереди, затраты времен центрального процессора, сеанс телефонной связи и т.д.
Если мы распределяем коэффициент веса времени "жизни" пропорционально его продолжительности, то средний вес всех временных интервалов становится равным средней величине
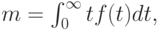 |
( 3.21) |
где  - вероятность наблюдения в пределах интервала
- вероятность наблюдения в пределах интервала 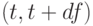 и
и  - вес этого наблюдения.
- вес этого наблюдения.
При обработке нагрузки нас интересует вычисление соотношения всей нагрузки, которая возникает в системе, и времени пребывания в системе заявок продолжительностью меньше, чем х:
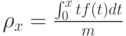 |
( 3.22) |
Это то же самое, что и соотношение средней величины нагрузки, которая возникает в системе, и времени "жизни" меньше, чем х.
Часто относительно небольшое время обслуживания позволяет обслужить относительно большую долю полной нагрузки. Из рис.3.2 мы видим, что если коэффициент формы 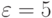 , то 75 % времен обслуживания вносят только 30 %-ую долю полной нагрузки (правило Вильфредо Парето). Этот факт можно использовать и предоставлять приоритет коротким задачам без большой задержки более длинных задач (Лекция 13).
, то 75 % времен обслуживания вносят только 30 %-ую долю полной нагрузки (правило Вильфредо Парето). Этот факт можно использовать и предоставлять приоритет коротким задачам без большой задержки более длинных задач (Лекция 13).
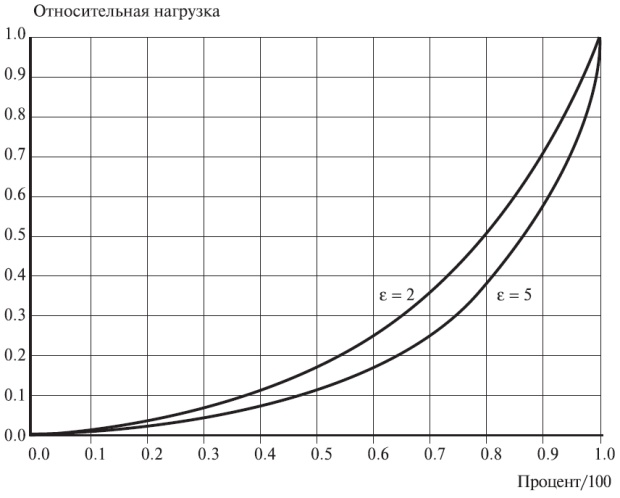
Рис. 3.2. Пример величины относительной нагрузки в зависимости от времени пребывания в системе, согласно уравнению (3.22).
Здесь  соответствует показательному распределению, а
соответствует показательному распределению, а 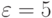 соответствует принципу Парето. Мы обращаем внимание, что 10% наибольших времен пребывания в системе вносят вклад от 33 % до 47 %, нагрузки (сравните математические ожидания времени обслуживания клиента и среднее время ожидания в Лекции 5)
соответствует принципу Парето. Мы обращаем внимание, что 10% наибольших времен пребывания в системе вносят вклад от 33 % до 47 %, нагрузки (сравните математические ожидания времени обслуживания клиента и среднее время ожидания в Лекции 5)
