| Стоимость "обучения" |
Теория вероятностей и статистика
Прямое время возвращения
Остаток времени "жизни", отсчитываемый от случайной точки времени, называется прямым временем возвращения. В этой секции мы получим некоторую важную формулу. Чтобы сформулировать проблему, рассмотрим пример. Мы желаем исследовать распределение времени "жизни" различных марок автомобилей, и опросить выбранных наугад автомобильных владельцев о возрасте их автомобиля. Так как точка времени опроса выбрана наугад, вероятность выбора автомобиля пропорциональна полному времени "жизни" автомобиля. Распределение будущего времени остатка "жизни" тогда будет идентично с уже достигнутым временем "жизни".
Составляя выборку таким способом, мы увидим, что вероятность выбора автомобиля определенной марки пропорциональна времени "жизни" автомобиля, то есть мы предпочтительно выберем автомобили с более длинными сроками службы (выбор, базирующийся на длине срока службы). Вероятность выбора автомобиля, имеющего полное время "жизни"  , дается с помощью приведенной ниже формулы (момент распределение в статистике) (дифференцирование (3.22):
, дается с помощью приведенной ниже формулы (момент распределение в статистике) (дифференцирование (3.22):
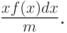
Так как мы рассматриваем случайную точку времени, распределение остающегося времени "жизни" будет однородно распределено в промежутке 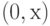 :
:
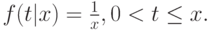
Тогда функция плотности остающегося времени "жизни" в случайной точке времени следующая:
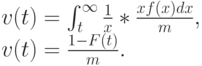 |
( 3.23) |
где F(t) - функция распределения полного времени "жизни" и m - средняя величина.
Применяя равенство (3.3), мы обращаем внимание, что  -тый момент
-тый момент 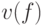 определяется с помощью
определяется с помощью  -того момента
-того момента 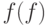 :
:
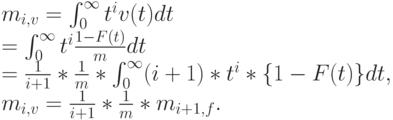 |
( 3.24) |
Мы получаем среднее значение
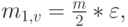 |
( 3.25) |
где является коэффициентом формы распределения "время жизни". Эта формула также действительна для дискретных распределений времени.
Распределение j'тых наибольших из к случайных переменных
Предположим, что к случайных переменных 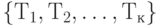 независимы и идентично распределены с функцией распределения
независимы и идентично распределены с функцией распределения 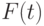 . Распределение
. Распределение  -той наибольшей переменной выглядит следующим образом:
-той наибольшей переменной выглядит следующим образом:
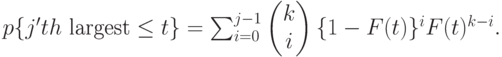 |
( 3.26) |
 переменных могут быть большими, чем
переменных могут быть большими, чем  . Меньшие переменные (или
. Меньшие переменные (или 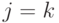 ) имеют функцию распределения:
) имеют функцию распределения:
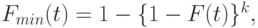 |
( 3.27) |
и наибольшая переменная 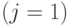 имеет функцию распределения
имеет функцию распределения
 |
( 3.28) |
Если случайные переменные имеют индивидуальные распределения функции 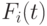 , мы получаем выражение, более сложное, чем (3.26). Для наименьшей и наибольшей переменной мы добираемся так:
, мы получаем выражение, более сложное, чем (3.26). Для наименьшей и наибольшей переменной мы добираемся так:
 |
( 3.29) |
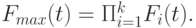 |
( 3.30) |
Комбинация случайных переменных
Мы можем комбинировать времена "жизни" случайных процессов, сочетая их последовательно или параллельно, либо применяя оба варианта.
Последовательные случайные переменные
Соединение последовательно  независимых временных интервалов соответствует сложению
независимых временных интервалов соответствует сложению  независимых случайных переменных, то есть свертыванию случайных переменных.
независимых случайных переменных, то есть свертыванию случайных переменных.
Если мы обозначаем среднюю величину и дисперсию  -того временного интервала соответственно
-того временного интервала соответственно 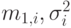 , тогда сумма случайных переменных имеет следующую среднюю величину и дисперсию:
, тогда сумма случайных переменных имеет следующую среднюю величину и дисперсию:
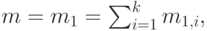 |
( 3.31) |
 |
( 3.32) |
Вообще, мы должны сложить так называемые кумулянты, или полуварианты ( cumulant ), и первые три кумулянта совпадают с первыми тремя центральными моментами.
Функция распределения суммы получена свертыванием:
 |
( 3.33) |
где  - оператор свертывания (Секция. 6.2.2).
- оператор свертывания (Секция. 6.2.2).
Пример 3.2.1: Биноминальное распределение и испытания Бернулли
Пусть вероятность успеха в испытании (например, бросание кубика при игре в кости) равна р, а вероятность отказа равняется 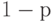 . Число успехов в единственном испытании тогда получается с помощью распределения Бернулли:
. Число успехов в единственном испытании тогда получается с помощью распределения Бернулли:
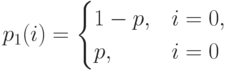 |
( 3.34) |
Если мы проведем  испытаний, то биноминальное распределение числа успехов
испытаний, то биноминальное распределение числа успехов
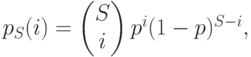 |
( 3.35) |
получается сборкой  распределений Бернулли. Если мы делаем одно дополнительное испытание, то распределение общего количества успехов получается сверткой Биноминального распределения (3.35) и Распределения Бернулли (3.34):
распределений Бернулли. Если мы делаем одно дополнительное испытание, то распределение общего количества успехов получается сверткой Биноминального распределения (3.35) и Распределения Бернулли (3.34):
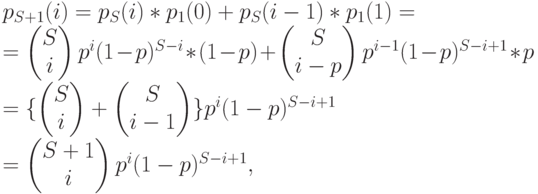
что и требовалось доказать.
Параллельные случайные переменные
Взвешивание l независимых случайных переменных, где  -тая переменная появляется с весовым коэффициентом
-тая переменная появляется с весовым коэффициентом 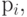 дает
дает
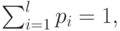
а средняя величина 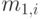 , и дисперсия
, и дисперсия 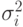 сумма случайных переменных имеет следующую среднюю величину и дисперсию:
сумма случайных переменных имеет следующую среднюю величину и дисперсию:
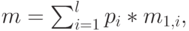 |
( 3.36) |
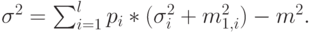 |
( 3.37) |
В этом случае мы должны взвесить нецентральные моменты. Для  -того момента мы имеем:
-того момента мы имеем:
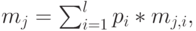 |
( 3.38) |
где 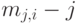 -тый нецентральный момент распределения
-тый нецентральный момент распределения  -того интервала.
-того интервала.
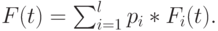 |
( 3.39) |
Подобная формула справедлива для функции плотности:

Взвешенная сумма распределений называется составным распределением.
Стохастическая сумма
Под стохастической суммой мы понимаем сумму стохастических случайных переменных (Feller, 1950 [27]). Рассмотрим группу направлений без перегрузки, где процесс поступления вызовов и времена пребывания в системе стохастически независимы. Если мы рассматриваем фиксированный временной интервал  , то число поступления заявок - случайная переменная
, то число поступления заявок - случайная переменная  . Ниже переведены свойства числа
. Ниже переведены свойства числа 
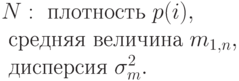 |
( 3.40) |
Число поступлений вызовов  имеет время пребывания в системе
имеет время пребывания в системе 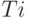 Все
Все 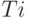 имеют одно и то же самое распределение, и каждое поступление (запрос) прибавляет некоторое число единиц времени (времени пребывания в системе), которые являются случайными переменными со следующими характеристиками.
имеют одно и то же самое распределение, и каждое поступление (запрос) прибавляет некоторое число единиц времени (времени пребывания в системе), которые являются случайными переменными со следующими характеристиками.
 |
( 3.41) |
Весь объем нагрузки, который получен из-за поступления заявок (запросов), пребывающих в пределах рассматриваемого временного интервала  , - случайная переменная:
, - случайная переменная:
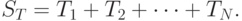 |
( 3.42) |
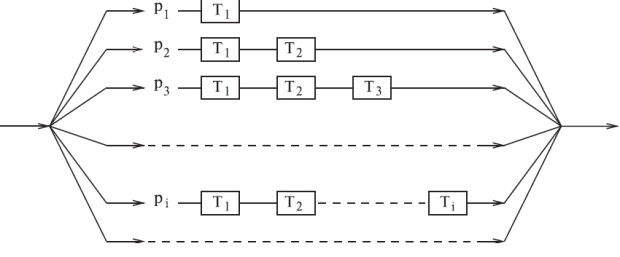
Рис. 3.3. Стохастическая сумма может интерпретироваться как комбинация последовательно/параллельных случайных переменных.
Далее мы принимаем, что 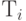 , и
, и  стохастически независимы. Это условие выполняется при условии нулевой перегрузки.
стохастически независимы. Это условие выполняется при условии нулевой перегрузки.
Следующие выводы правильны и для дискретных, и для непрерывных случайных переменных (суммирование можно заменить интеграцией или наоборот). Стохастическая сумма становится последовательной и параллельной комбинацией случайных переменных, как показано на рис.3.3. Для данной ветви i мы находим (рис.3.3):
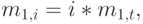 |
( 3.43) |
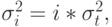 |
( 3.44) |
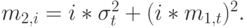 |
( 3.45) |
Суммируя по всем возможным значениям (ветвям)  , мы получаем:
, мы получаем:
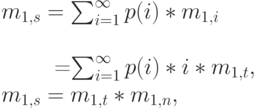 |
( 3.46) |
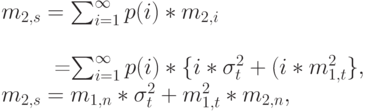 |
( 3.47) |
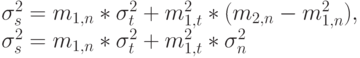 |
( 3.48) |
Можно отметить, что есть два элемента, составляющие полную дисперсию: один элемент отображает, что число вызовов - случайная переменная ( 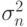 ), и второй - что продолжительность вызовов - случайная переменная (
), и второй - что продолжительность вызовов - случайная переменная ( 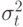 ).
).
Пример 3.3.1: Специальный случай 1: N = n = constant (m = п)
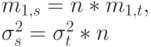 |
( 3.49) |
Это соответствует числу вызовов поступющих в одно и то же время, при измерении объема трафика мы можем оценить среднее время удержания.
Пример 3.3.2: Специальный случай 1:T=t = constant (m = t)
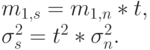 |
( 3.50) |
Если мы изменяем масштаб от 1 до 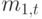 , то среднее значение есть произведение
, то среднее значение есть произведение 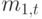 на дисперсию
на дисперсию 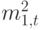 При среднем числе вызовов
При среднем числе вызовов 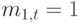 расчет числа вызовов является проблемой.
расчет числа вызовов является проблемой.
Пример 3.3.3: Стохастические суммы
Возьмем пример, не относящийся к телетрафику.  будет обозначить число ливневых дождей в течение одного месяца, а
будет обозначить число ливневых дождей в течение одного месяца, а 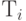 - обозначить количество осадков одного
- обозначить количество осадков одного  -того ливня.
-того ливня. 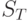 тогда - случайная переменная, описывающая полное количество осадков в течение месяца.
тогда - случайная переменная, описывающая полное количество осадков в течение месяца.
 может также означать для данного временного интервала число несчастных случаев, зарегистрированных страховой компанией, а
может также означать для данного временного интервала число несчастных случаев, зарегистрированных страховой компанией, а 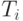 -компенсацию за
-компенсацию за  -ый несчастный случай.
-ый несчастный случай. 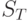 тогда - общая сумма, заплаченная компанией в течение рассмотренного периода.
тогда - общая сумма, заплаченная компанией в течение рассмотренного периода.
Краткие итоги
- Все временные интервалы, поступления и обслуживания вызовов (времена блокировки, времена занятости, время занятия Центрального процессора ( CPU )) могут быть выражены неотрицательными случайными переменными.
- Временной интервал может быть описан случайной переменной
 , которая может быть охарактеризована функцией распределения
, которая может быть охарактеризована функцией распределения 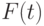 .
. - Обычно мы принимаем, что время обслуживания является независимым от времени момента поступления вызова, и что время обслуживания не зависит от времен обслуживания других вызовов.
- Распределение обычно однозначно определяется всеми его моментами. Средняя величина (математическое ожидание) - это первый момент. Дисперсия - 2-ой центральный момент
- Мера нерегулярности функции распределения определяется также отклонением распределения от средней величины - коэффициентом вариации, коэффициентом формы Пальма.
- Фундаментальная характеристика показательного (экспоненциального) распределения называется Марковским или свойством без последействия (при отсутствии памяти (возраста)) - время жизни не зависит от момента поступления заявки.
- Если мы распределяем коэффициент веса времени "жизни" пропорционально его продолжительности, то средний вес всех временных интервалов становится равным средней величине.
- Времена обслуживания большого числа вызовов составляют малую долю полной нагрузки (правило Вильфредо Парето). Этот факт можно использовать и предоставлять приоритет коротким задачам без большой задержки более длинных задач.
- Остаток времени "жизни", отсчитываемый от случайной точки времени, называется прямым временем возвращения.
- Если вероятность успеха в испытании (например, бросание кубика при игре в кости) равна р, вероятность отказа равняется
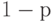 . Число успехов в единственном испытании тогда получается с помощью распределения Бернулли.
. Число успехов в единственном испытании тогда получается с помощью распределения Бернулли. - Средняя величина
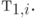 и дисперсия
и дисперсия 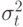 суммы параллельных случайных величин определяется взвешиванием
суммы параллельных случайных величин определяется взвешиванием  независимых случайных переменных, где
независимых случайных переменных, где  -тая переменная используется с весовым коэффициентом
-тая переменная используется с весовым коэффициентом 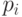 .
. - Есть два элемента стохастическая суммы, составляющие полную дисперсию: один элемент отображает, что число вызовов - случайная переменная (
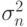 ), и второй элемент - что продолжительность вызовов - случайная переменная (
), и второй элемент - что продолжительность вызовов - случайная переменная ( 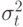 ).
).
