| Стоимость "обучения" |
Прикладная теория организации очередей
Классификация моделей организации очередей
В этой секции мы введем компактные системы обозначений для систем организации очереди, названных системой обозначений Кендалла.
Описание нагрузки и структуры
D.G. Kendall (1951 [61] ) ввел следующую систему обозначений для моделей организации очереди:
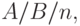
где:
 - процесс поступления вызовов,
- процесс поступления вызовов,
 - распределение времени обслуживания,
- распределение времени обслуживания,
 - число обслуживающих приборов.
- число обслуживающих приборов.
Для различных типов обрабатываемой нагрузки мы используем следующие стандартные системы обозначений (см. секцию 4.5).
 - Марковский. Экспоненциальные временные интервалы (Пуассоновский поток вызовов, экспоненциально распределенные времена обслуживания).
- Марковский. Экспоненциальные временные интервалы (Пуассоновский поток вызовов, экспоненциально распределенные времена обслуживания).
 - детерминированный. Постоянное время занятия оборудования.
- детерминированный. Постоянное время занятия оборудования.
 -
-  -Эрланговское распределение временных интервалов (
-Эрланговское распределение временных интервалов (  ).
).
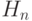 - гиперэкспоненциальный тип порядка n, распределенные временные интервалы.
- гиперэкспоненциальный тип порядка n, распределенные временные интервалы.
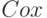 - Кокс - распределенные временные интервалы.
- Кокс - распределенные временные интервалы.
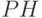 - распределения временных интервалов фазового типа.
- распределения временных интервалов фазового типа.
 - произвольный поток, произвольное время обслуживания (допускает корреляцию между соседними интервалами).
- произвольный поток, произвольное время обслуживания (допускает корреляцию между соседними интервалами).
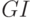 - рекуррентный поток (длительности соседних интервалов статистически независимы и имеют одинаковое распределение), возобновляемый процесс поступления заявок.Повторные вызовы).
- рекуррентный поток (длительности соседних интервалов статистически независимы и имеют одинаковое распределение), возобновляемый процесс поступления заявок.Повторные вызовы).
Пример 13.1.1: Обычные модели организации очередей
 - чистая система с ожиданием с Пуассоновским потоком вызовов, экспоненциально распределенными временами обслуживания и n обслуживающими приборами. Это классическая Эрланговская система с ожиданием (Лекция 12).
- чистая система с ожиданием с Пуассоновским потоком вызовов, экспоненциально распределенными временами обслуживания и n обслуживающими приборами. Это классическая Эрланговская система с ожиданием (Лекция 12).
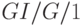 - рекуррентный входной поток, с произвольным временем обслуживания, ожиданием, и только одним обслуживающим прибором. Вышеупомянутая система обозначений широко используется в литературе. Для полной спецификации системы организации очереди требуется больше информации:
- рекуррентный входной поток, с произвольным временем обслуживания, ожиданием, и только одним обслуживающим прибором. Вышеупомянутая система обозначений широко используется в литературе. Для полной спецификации системы организации очереди требуется больше информации:
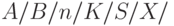
где:
 - полная емкость системы, или число мест ожидания,
- полная емкость системы, или число мест ожидания,
 - размер системы (число клиентов),
- размер системы (число клиентов),
 - дисциплина организации очереди (секция 13.1.2).
- дисциплина организации очереди (секция 13.1.2).
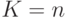 соответствует системе с потерями, которая часто обозначается как
соответствует системе с потерями, которая часто обозначается как 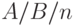 - Loss (Потери).
- Loss (Потери).
Верхний индекс  над
над  или, соответственно, над
или, соответственно, над  , указывает тип поступления вызовов (поступление навалом, пакетное поступление), соответственно обслуживание группы.
, указывает тип поступления вызовов (поступление навалом, пакетное поступление), соответственно обслуживание группы.  (Clocked -Тактируемый) может указать, что система работает в дискретное время. Обычно принимается полная доступность.
(Clocked -Тактируемый) может указать, что система работает в дискретное время. Обычно принимается полная доступность.
Стратегия организации очередей: дисциплины и организация
Клиенты, стоящие в очереди на обслуживание, могут быть выбраны для обслуживания в соответствии со многими различным принципами. Мы сначала рассмотрим три классических дисциплины организации очереди.
FCFS (First Come - First Served): "Первый Пришел - Первый Обслужен".
Она также называется справедливой очередью или упорядоченной очередью. На практике, когда клиенты - люди, эта дисциплина часто предпочитается другим. Она также называется в порядке поступления. Часто она обозначается FIFO: First In - First Out ("Первый на Входе - Первый на Выходе").
Обратите внимание, что дисциплина в порядке поступления рассматривается только по отношению к очереди, а к не полной системе. Если мы имеем больше чем один обслуживающий прибор, то клиент с небольшим временем обслуживания может "догнать" клиента с большим временем ожидания, даже если мы используем дисциплину очереди в порядке поступления.
LCFS (Last Come - First Served): "Последний Пришел - Первый Обслужен".
Эта дисциплина соответствует принципу стека. Она, например, используется при хранении, на полках магазинов и т.д. Также она называется "дисциплина обслуживания в магазинном порядке". Иногда она обозначается LIFO ( Last In - First Out: "Последний на Входе - Первый на Выходе").
SIRO (Service In Random Order): Обслуживание в Случайном Порядке.
Все клиенты, стоящие в очереди, имеют одинаковую вероятность быть выбранным для обслуживания. Она также называется случайной (RANDOM или RS (Random Selection)).
Первые две дисциплины учитывают времена поступления, а третий не рассматривает никаких критериев вообще и поэтому не требует никакой памяти (в отличие от первых двух).
Они могут быть реализованы с помощью простых технических систем. Например, в электромеханической телефонной станции дисциплина организации очереди SIRO часто использовалась сходным образом с последовательным поиском без возвращения.
Для трех вышеупомянутых дисциплин полное время ожидания для всех клиентов одно и тоже. Дисциплина организации очереди лишь решает, как время ожидания распределено между отдельными клиентами. В управляемой программой системе организации очереди могут быть более сложные дисциплины. В теории организации очереди мы вообще принимаем, что полная предложенная нагрузка не зависит от дисциплины организации очереди.
Для компьютерных систем мы часто пробуем уменьшить полное время ожидания. Это может быть сделано с использованием следующих дисциплин, учитывающих критерии времени обслуживания.
SJF (Shortest Job First): "Первым - Самое короткое Задание", она же обозначается SJN (Shortest Job Next - "Следующее - Самое короткое Задание") или SPF (Shortest Processing time First - "Сначала - Самое короткое время Обработки" ). Дисциплина предполагает, что мы заранее знаем время обслуживания и это минимизируем полное время ожидания для всех клиентов.
Вышеупомянутые дисциплины принимают во внимание или время поступления заявки, или время обслуживания. Компромисс между ними получается в следующих дисциплинах.
Round Robin: Циклическая (круговая система), при которой обслуживаемому клиент определяется самое большее фиксированное время обслуживания (отрезок времени или слот). Если обслуживание не заканчивается в течение этого интервала, клиента возвращают в очередь типа FCFS.
PS: Processor Sharing: Совместное использование Процессора. Все клиенты совместно используют производительность.
FB- Foreground / Background: Передняя позиция / Задняя позиция.
Эта дисциплина, не зная заранее времена обслуживания, пробует осуществлять дисциплину SJF. Сервер предлагает обслуживание клиенту, который до сих пор обслуживался меньшее время. Когда все клиенты обслужены за равное время обслуживания, FB становится идентичной с PS (Processor Sharing).
Последние упомянутые дисциплины являются динамическими, так как дисциплины организации очереди зависят от времени, затраченного на обслуживания.
Приоритет клиентов
На практике клиенты часто разделяются на  приоритетных классов, где клиент, принадлежащий классу
приоритетных классов, где клиент, принадлежащий классу  , имеет более высокий приоритет, чем клиент, принадлежащий классу
, имеет более высокий приоритет, чем клиент, принадлежащий классу  . Мы различаем два типа приоритета.
. Мы различаем два типа приоритета.
Неприоритетное обслуживание (Non-preemptive)
Поступивший вызов с более высоким приоритетом, чем обслуживаемый клиент, ждет до конца обслуживания, пока сервер будет свободен (и все клиенты с более высоким приоритетом будут обслужены). Это дисциплина также называется HOL (Head-Of-the-Line - "Во главе очереди").
Приоритетное обслуживание (Preemptive)
Если обслуживаемый клиент имеет более низкий приоритет, чем новый поступивший вызов, то обслуживание прерывается. При этом возможны следующие способы возвращения к работе:
- приоритетное возвращение к работе PR (Preemptive resume), после прерывания обслуживание прерванного вызова продолжается, при этом имеются варианты:
- приоритетное без повторения (Preemptive without re-sampling), обслуживание перезапускается, начиная с того самого момента, на котором оно было прервано.
- приоритетное с повторением (Preemptive with re-sampling), обслуживание начинается снова с новым временем обслуживания.
Две последних дисциплины применяются, например, в производственных системах и при обеспечении надежности. В пределах отдельных классов мы упоминали эти дисциплины в секции 13.1.2.
В литературе, посвященной организации очереди, мы встречаем много других стратегий и обозначений. GD обозначает произвольную дисциплину организации очереди (general discipline).
Поведение клиентов является также предметом моделирования.
Отказывающийся становиться в очередь - применяется к системам организации очереди, где клиенты с вероятностью, которая зависит от длины очереди, могут отказаться от присоединения к очереди.
Нарушающий очередь - применяется к системам с нетерпеливыми клиентами, которые уходят из очереди без обслуживания.
Перепрыгивающий - применяется к системам, где клиенты могут "перепрыгнуть" из одной, например, длинной, очереди в другую - короткую очередь.
Таким образом, есть много возможных различных моделей. В этой лекции мы будем иметь дело только с самыми важными моделями и обычно будем рассматривать системы с одним обслуживающим прибором.
Пример 13.1.2: Система коммутации с программным обеспечением (Накопленная Управляемая Программа (SPC)
В SPC (Stored Program Controlled) задачи систем процессоров разделены, скажем, на десять приоритетных классов. Приоритет, например, обновляется каждые 5 миллисекунд. Сообщения об ошибках от процессора имеют самый высокий приоритет, тогда как стандартные задачи управления имеют самый низкий приоритет. Обслуживание принятых вызовов имеет более высокий приоритет, чем обнаружение новых попыток вызова.
