| Стоимость "обучения" |
Системы с ожиданием
Состояния терминалов и характеристики нагрузки
Характеристики качества работы легко могут быть получены на основе аналогии с классической системой с потерями Эрланга (12.37). Заменяя  на
на 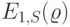 , получаем, что компьютер работает с вероятностью
, получаем, что компьютер работает с вероятностью 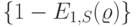 . Тогда среднее число терминалов, обслуживаемых компьютером, равно:
. Тогда среднее число терминалов, обслуживаемых компьютером, равно:
 |
( 12.38) |
Среднее число ожидающих терминалов равно:
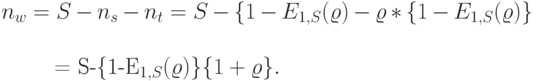 |
( 12.40) |
Если мы рассматриваем случайный терминал в случайный момент времени, то получаем:
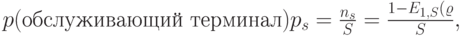 |
( 12.41) |
 |
( 12.42) |
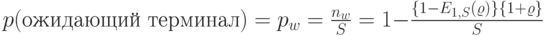 |
( 12.43) |
Мы также интересуемся временем реакции  , которая имеет среднюю величину
, которая имеет среднюю величину  Применяя формулу Литла
Применяя формулу Литла  к терминалам, установленным на ожидание, и к компьютеру, мы, соответственно, получаем (обозначая скорость обращения заявок
к терминалам, установленным на ожидание, и к компьютеру, мы, соответственно, получаем (обозначая скорость обращения заявок  ):
):
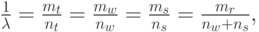 |
( 12.44) |
или
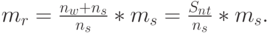
Используя (12.38) и (12.44) 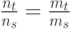 , мы получим:
, мы получим:
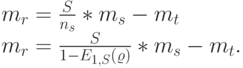 |
( 12.45) |
Таким образом, среднее время ответа не зависит от типа распределения времени, поскольку оно базируется на формуле Литла (12.38) и (12.44). Однако, 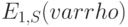 будет зависеть от типов распределений, так же, как это было в B-формуле Эрланга. Если время обслуживания компьютера является экспоненциально распределенным (средняя величина
будет зависеть от типов распределений, так же, как это было в B-формуле Эрланга. Если время обслуживания компьютера является экспоненциально распределенным (средняя величина 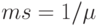 ), то
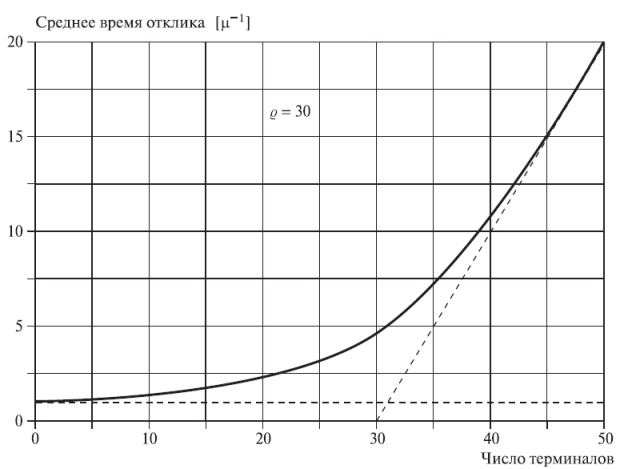
), то 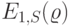 будет определяться формулой (12.37). Pис.12.8 в этом случае показывает время реакции как функцию числа терминалов.
будет определяться формулой (12.37). Pис.12.8 в этом случае показывает время реакции как функцию числа терминалов.
Если все временные интервалы являются постоянными, то компьютер может работать без пауз, обслуживая  терминалов без всякой задержки, когда:
терминалов без всякой задержки, когда:
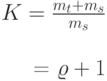 |
( 12.46) |
 - подходящий параметр для описания точки насыщения системы. Среднее время ожидания для произвольного терминала может быть получено из (12.45):
- подходящий параметр для описания точки насыщения системы. Среднее время ожидания для произвольного терминала может быть получено из (12.45):
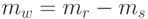
Сервисный коэффициент -  = 30. Среднее время реакции переходит в прямую линию, пересекающую ось
= 30. Среднее время реакции переходит в прямую линию, пересекающую ось  при
при  терминалов. Среднее виртуальное время реакции для системы с S терминалами равно фактическому среднему времени реакции для системы с
терминалов. Среднее виртуальное время реакции для системы с S терминалами равно фактическому среднему времени реакции для системы с 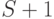 терминалами (теорема моментов поступления, теорема 8.1).
терминалами (теорема моментов поступления, теорема 8.1).
Пример 12.5.2: Компьютер в режиме разделения времени
В системе, обслуживающей терминалы, компьютер иногда свободен (ждет заявок от терминалов), а иногда терминалы ждут компьютер. Если терминалов мало, результатом будет низкое использование компьютера, тогда как если подключено много терминалов, то пользователи будут тратить время впустую на ожидание.
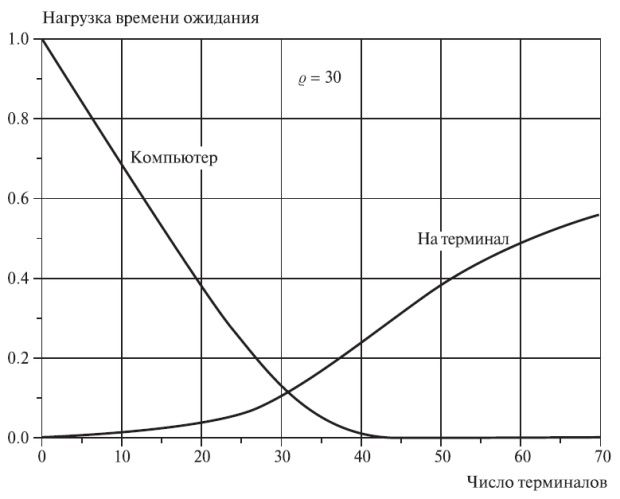
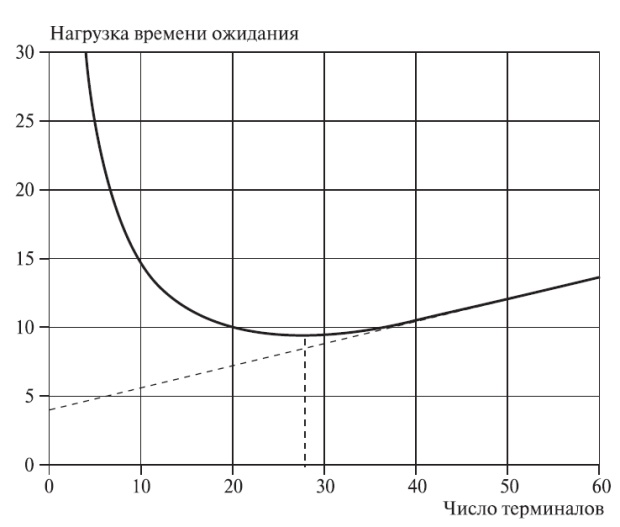
Pис.12.9 показывает нагрузку времени ожидания в Эрл для компьютера и для одного терминала. Соответствующая надбавка затрат и сумма времен ожидания для компьютера и для всех терминалов дает стоимость ожидания.
Нагрузка времени ожидания (соотношение времени, потраченного на ожидание), измеренная в Эрл для компьютера и соответственно для терминалов при интерактивной системе организации очереди (коэффициент обслуживания -  = 30).
= 30).
Например, на рис.12.9 мы получаем минимальные полные затраты ожидания приблизительно для 45 терминалов. Стоимость ожидания компьютера - в сотню раз больше стоимости времени одного терминала. При 31 терминале и одном компьютере каждый терминал тратит 11,4 % времени для ожидания. Если отношение стоимости - 31, то 31 - оптимальное число терминалов. Однако должны быть учтены несколько других факторов.
Пример 12.5.3: Потери по нагрузке
Мы можем определить потери по нагрузке обычным способом (секция 2.3). Предложенная нагрузка - это нагрузка, которая будет при отсутствии очереди.
Удельная нагрузка будет (8.8):
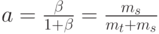
На один источник обслуженная нагрузка:
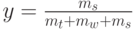
Потери по нагрузке равны:
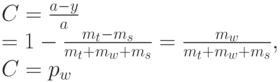
Потери по нагрузке становятся равными соотношению времени, потраченного на ожидание. Для системы Эрланга с ожиданием потери по нагрузке являются нулевыми, потому что вся предложенная нагрузка обслуживается.
Модель восстановления машин с п серверами
Вышеупомянутая модель легко может быть обобщена на  компьютеров.
компьютеров.
Диаграмма переходов показана на рис.12.10 Вероятности устойчивых состояний равны:
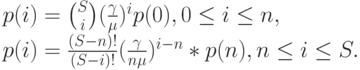 |
( 12.47) |
где мы имеем нормировочное ограничение:
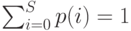 |
( 12.48) |
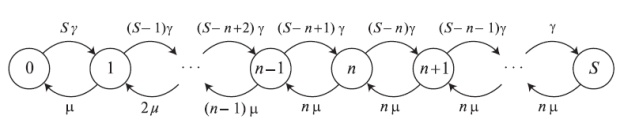
Рис. 12.10. Диаграмма переходов состояний для модели восстановления машин с S терминалами и n компьютерами
Можно показать, что вероятности состояния не зависят от распределения времени паузы (размышление или работа с терминалом), как и в случае с одним компьютером. (Мы получаем Пуассоновский поток вызовов, зависимый от состояния).
Произвольный терминал - в случайный момент времени может находиться в одном из трех возможных состояний:
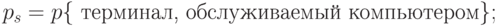


Мы имеем:
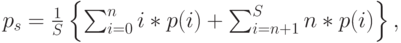 |
( 12.49) |
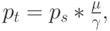 |
( 12.50) |
 |
( 12.51) |
Среднее использование компьютеров равно:
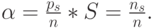 |
( 12.52) |
Среднее время ожидания для терминала равно:
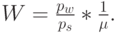 |
( 12.53) |
Иногда 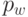 называют коэффициентом потерь терминалов, и аналогично
называют коэффициентом потерь терминалов, и аналогично  называют коэффициентом потерь компьютеров (рис.12.9).
называют коэффициентом потерь компьютеров (рис.12.9).
Пример 12.5.4: Числовой пример
Следующие числовые примеры иллюстрируют то, что мы получаем самое высокое использование для больших значений  (и
(и  ). Рассмотрим систему с
). Рассмотрим систему с 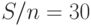 и
и 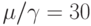 для большого числа компьютеров (в этом случае
для большого числа компьютеров (в этом случае  ).
).
 |
1 | 2 | 4 | 8 | 16 |
|---|---|---|---|---|---|
 |
0.0289 | 0.0300 | 0.0307 | 0.0313 | 0.0316 |
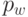 |
0.1036 | 0.0712 | 0.0477 | 0.0311 | 0.0195 |
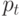 |
0.8675 | 0.8989 | 0.9215 | 0.9377 | 0.9489 |
 |
0.8675 | 0.8989 | 0.9215 | 0.9377 | 0.9489 |
![W[\mu^1]](/sites/default/files/tex_cache/41e03d64e1070ff719f605c4f721449f.png) |
3.5805 | 2.3754 | 1.5542 | 0.9945 | 0.6155 |
Оптимизация модели восстановления машин
В этой секции мы оптимизируем модель восстановления машин тем же способом, как сделал это Пальм в 1947 г. Заметим, что модель для единственного ремонтника (одного обслуживающего прибора) похожа на систему с потерями Эрланга, которую мы оптимизировали в Лекции 7. Мы можем видеть, что одна и та же модель может быть оптимизирована несколькими способами.
Рассмотрим терминальную систему с одним компьютером и  терминалами и найдем оптимальное значение
терминалами и найдем оптимальное значение  . Примем следующую структуру затрат:
. Примем следующую структуру затрат:
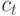 - стоимость на терминал в единицу времени при паузе (размышление или работа только с терминалом);
- стоимость на терминал в единицу времени при паузе (размышление или работа только с терминалом);
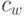 - стоимость на один терминал в единицу времени при ожидании;
- стоимость на один терминал в единицу времени при ожидании;
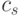 - стоимость на один терминал в единицу времени при обслуживании;
- стоимость на один терминал в единицу времени при обслуживании;
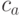 - стоимость на компьютер в единицу времени.
- стоимость на компьютер в единицу времени.
Предполагается, что стоимость компьютера не зависит от использования и разбита однородно по числу всех терминалов. Результат (конечный продукт) процесса - это некоторое время паузы (размышления и подготовки информации в терминалах) во время производства продукта.
Общая стоимость 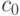 в единицу времени, когда терминал в паузе:
в единицу времени, когда терминал в паузе:
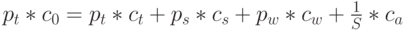 |
( 12.54) |
Модель восстановления машины. Общие стоимости, данные в (12.57), показывают общую стоимость как функцию числа терминалов для сервисного отношения 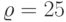 и отношения стоимости
и отношения стоимости 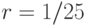 (см. рис. 7.6)
(см. рис. 7.6)
Мы хотим минимизировать  . Сервисное отношение
. Сервисное отношение  равно
равно 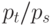 . Вводя отношение стоимости
. Вводя отношение стоимости  получаем:
получаем:
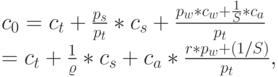 |
( 12.55) |
Это выражение должно быть свернуто как функция S. Учитывая, что только последний член зависит от числа терминалов, получаем:
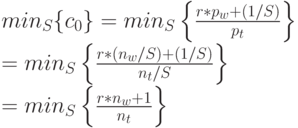 |
( 12.56) |
![=min_S \left \{ \frac{r[S-\{1-E_{1,S}(\varrho)\}\{1+ \varrho\}]+1}{\{1-E_{1,S}(\varrho)\}*\varrho}\right \}\\
=min_s \left \{ \frac{r*S+1}{\{1-E_{1,S}(\varrho)\}* \varrho}+1+\frac{1}{\varrho} \right \},](/sites/default/files/tex_cache/1ec506a43397c37965a0b00c198a3278.png) |
( 12.57) |
Мы замечаем, что минимум не зависит от 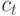 и
и 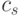 и что только отношение
и что только отношение  содержит характеристики стоимости. Числитель соответствует (7.31), тогда как знаменатель соответствует обслуженной нагрузке в соответствующей системе с потерями. Таким образом мы минимизируем стоимость обслуживания в Эрл. для соответствующей системе с потерями. На рис.12.10 показан пример. Мы замечаем, что результат отличается от результата, полученного с использованием принципа Мо для системы с потерями Эрланга (рис.7.6), где мы оптимизируем прибыль.
содержит характеристики стоимости. Числитель соответствует (7.31), тогда как знаменатель соответствует обслуженной нагрузке в соответствующей системе с потерями. Таким образом мы минимизируем стоимость обслуживания в Эрл. для соответствующей системе с потерями. На рис.12.10 показан пример. Мы замечаем, что результат отличается от результата, полученного с использованием принципа Мо для системы с потерями Эрланга (рис.7.6), где мы оптимизируем прибыль.
Краткие итоги
- В этой лекции рассматривается система с ожиданием, имеющая бесконечное число мест ожидания. Когда все
 обслуживающих приборов заняты, поступивший вызовов ставится в очередь и ждет, пока не освободится хотя бы один обслуживающий прибор.
обслуживающих приборов заняты, поступивший вызовов ставится в очередь и ждет, пока не освободится хотя бы один обслуживающий прибор. - Когда хотя бы один обслуживающий прибор свободен, клиенты не могут оставаться в очереди (полная доступность).
o Рассмотрены два случая потоков нагрузки, Пуассоновский поток вызовов ( бесконечное число источников ) и экспоненциально распределенное время обслуживания ( PCT-I ) - Эрланговская система с ожиданием (
 ).
). - Также рассмотрены ограниченное число источников и экспоненциально распределенное время обслуживания ( PCT-II ). Это - модель Пальма, называемая моделью восстановления машин.
-
Система с ожиданием типа
 обслуживает Пуассоновский поток вызовов (
обслуживает Пуассоновский поток вызовов (  ) и имеет экспоненциальные время обслуживания (
) и имеет экспоненциальные время обслуживания (  ) и
) и  обслуживающих приборов при бесконечном числе мест ожидания.
обслуживающих приборов при бесконечном числе мест ожидания. - Состояние системы определяется как общее количество пользователей в системе (или в обслуживании, или ожидающих в очереди).
-
Вероятность, что система c ожиданием находится в состоянии
 , равна
, равна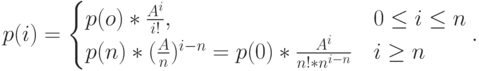
где
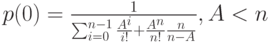 .
. -
Вероятность ожидания
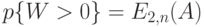 в системе c ожиданием равна:
в системе c ожиданием равна: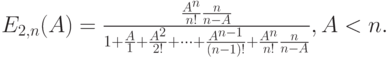
( формула Эрланга для систем с ожиданием ).
-
Поскольку мы имеем очень точную рекурсивную формулу для числовой оценки B-формулы (7.29) Эрланга, можно использовать следующие отношения для того, чтобы получить числовые значения для C-формулы:

- Мы должны отличать длину очереди в произвольный момент времени и длину очереди, когда есть клиенты, стоящие в очереди.
-
Длина очереди
 в произвольной момент времени называется виртуальной длиной очереди. Эта длина очереди определяется для произвольного клиента:
в произвольной момент времени называется виртуальной длиной очереди. Эта длина очереди определяется для произвольного клиента:
-
Средняя длина очереди со временем ожидания больше нуля (длина очереди, когда есть клиенты, стоящие в очереди):
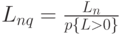
где
 - случайная переменная, обозначающая длину очереди.
- случайная переменная, обозначающая длину очереди. -
Теорема Литла говорит, что средняя длина очереди в произвольный момент времени равна интенсивности прибытия, умноженной на среднее время ожидания:

- Представляют интерес две характеристики: среднее время ожидания
 для всех клиентов и среднее времени ожидания
для всех клиентов и среднее времени ожидания  для клиентов, для которых время ожидания имеет положительное значение.
для клиентов, для которых время ожидания имеет положительное значение. -
Среднее время обслуживания для системы равно:
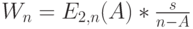 .
. -
Среднее время ожидания
 для задержанных вызовов:
для задержанных вызовов: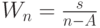 .
. -
Mo предложил свой принцип для систем организации очереди. Согласно этому принципу оптимальное решение равно:
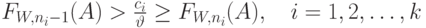
где
 - переменная стоимость канала;
- переменная стоимость канала;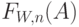 - функция увеличения времени ожидания;
- функция увеличения времени ожидания; - Системы организации очереди, где дисциплина обслуживания зависит от времени поступления вызовов, все имеют одни и те же средние времена ожидания. В этом случае стратегия оказывает влияние только на распределение времен ожидания для каждого отдельного клиента.
- Вероятность
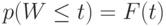 , что положительное время ожидания
, что положительное время ожидания  превосходит заданную величину, равна вероятности, что в Пуассоновском потоке вызовов с интенсивностью
превосходит заданную величину, равна вероятности, что в Пуассоновском потоке вызовов с интенсивностью 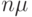 , по крайней мере,
, по крайней мере, 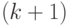 вызовов поступят в течение интервала
вызовов поступят в течение интервала  .
. - Исследование распределения времени ожидания упрощается в случае дисциплины (First Come First Served - "Первый прибыл - Первый обслужен"). Та же дисциплина обозначается FIFO (First In First Out). Эта дисциплина также называется дисциплина обслуживания в порядке поступления.
-
При поступлении вызова в систему с ожиданием и дисциплиной обслуживания FCFS со всеми ранее занятыми обслуживающими приборами можно:
- рассчитать число
 ждущих клиентов. Полное время ожидания тогда будет
ждущих клиентов. Полное время ожидания тогда будет 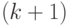 - Эрланговское распределение;
- Эрланговское распределение; - если не учитывать этих ждущих клиентов, то время ожидания становится экспоненциально распределенным.
- рассчитать число
-
Среднее время пребывания заявки в системе в случае одного обслуживающего прибора:
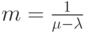
- Режим разделения времени - это лучшее решение для оптимального обслуживания большой группы источников нагрузки, использующих, например, терминалы, подключенные к универсальному компьютеру.
- Вероятности состояния модели ремонта машин с одним компьютером и
 терминалами справедливы в течение произвольных времен пауз (размышления и работа с компьютером), когда времена обслуживания компьютером являются экспоненциально распределенными.
терминалами справедливы в течение произвольных времен пауз (размышления и работа с компьютером), когда времена обслуживания компьютером являются экспоненциально распределенными. - Модель ремонта машин легко может быть обобщена на
 компьютеров и может быть оптимизирована для терминальной системы с одним компьютером и
компьютеров и может быть оптимизирована для терминальной системы с одним компьютером и  терминалами.
терминалами.

 (тета) -
(тета) -