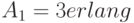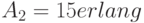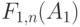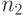| Стоимость "обучения" |
Планирование телекоммуникационных сетей
Пучок резервных каналов
В иерархических телекоммуникационных сетях с альтернативной маршрутизацией мы защищаем от потерь первичную нагрузку. Если рассматривать часть сети (рис.11.1), то можно убедиться, что прямая нагрузка AT конкурирует за свободные каналы пучка каналов группы AT с потерянной нагрузкой на участке AB. Как нагрузка, AB уже имеет прямой маршрут, но мы хотим дать приоритет нагрузке AT для доступа к каналам пучка линий AT. Это может быть сделано, если ввести пучок резервных каналов. Мы позволяем нагрузке AB занимать AT -каналы, только если на направлении AT есть больше, чем  свободных каналов, (
свободных каналов, (  - параметр резервирования). Таким образом, нагрузка AT получает более высокий приоритет, чем нагрузка, поступающая от AB. Если все вызовы имеют одинаковое среднее время пребывания в системе (
- параметр резервирования). Таким образом, нагрузка AT получает более высокий приоритет, чем нагрузка, поступающая от AB. Если все вызовы имеют одинаковое среднее время пребывания в системе ( 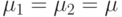 ) и односло-товую PCT-I нагрузку, то можно легко установить диаграмму переходов состояний и найти вероятность блокировки.
) и односло-товую PCT-I нагрузку, то можно легко установить диаграмму переходов состояний и найти вероятность блокировки.
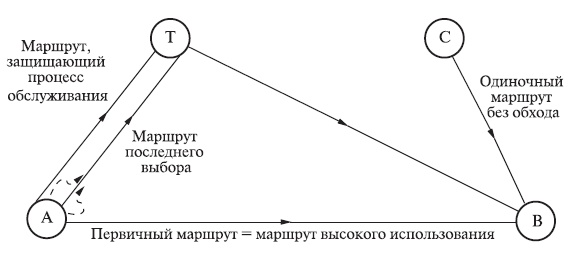
Рис. 11.1. Альтернативная маршрутизация нагрузки (см. пример 11.6.2). Нагрузка от A до B частично обслуживается прямым маршрутом (первичный маршрут = маршрут высокого использования), частично - вторичным маршрутом через транзитную станцию T.
Если отдельные потоки нагрузки имеют различные средние времена пребывания в системе либо если мы рассматриваем биноминальную нагрузку или нагрузку Паскаля, то нужно установить N-мерную диаграмму переходов состояний, которая будет необратима. При некоторых состояниях вызова, которые были приняты ранее, состояние может измениться, но изменения будут обнаружены, и таким образом процесс будет необратимым. Мы не можем применить алгоритм свертки, разработанный в секции 10.4 для этого случая, но обобщенный алгоритм в секции 10.5.2 может легко быть изменен, если принять, что 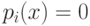 , когда
, когда 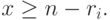
Основной недостаток метода резервного пучка линий в том, что он касается только местной стратегии, при которой рассматривают лишь одну группу пучков каналов (линий связи), а не полное соединение из "конца в конец". Кроме того, это односторонний механизм, который защищает один поток нагрузки за счет другого, но не наоборот. Поэтому он не может применяться для взаимной защиты соединений и услуг в широкополосных сетях.
Пример 11.6.1: Канал дежурного приема
В беспроводной подвижной системе связи мы можем гарантировать более низкую вероятность блокировки вызовов при хендовере (передаче вызова), чем для новых попыток вызова, резервируя последний свободный канал (называемый каналом дежурного приема) для вызовов хендовера.
11.6.2. Защита виртуального канала
При интегрированном обслуживании необходимо взаимно защитить все услуги от влияния друг на друга и гарантировать некоторый уровень обслуживания. Это может быть получено:
- некоторым минимальным распределением пропускной способности, которое гарантирует некоторое минимальное обслуживание, и
- максимальным распределением, которое учитывает преимущества статистического мультиплексирования и гарантирует, что не доминирует одна-единственная услуга. Эта стратегия имеет фундаментальную форму произведения, и вероятности состояния нечувствительны к распределению времени обслуживания. Также класс обслуживания (GoS) гарантируется не только для отдельного участка, но и из "конца в конец".
Принцип Мо
Теорема 11.1 - принцип Мо: оптимальное распределение ресурса получается при одновременном балансе предельных доходов и предельных затрат по всем секторам.
В этой секции мы представляем основные принципы Mo, изданные в 1924 г. Мы рассматриваем систему с некоторыми секторами, которые потребляют ресурсы (оборудование) для того, чтобы произвести продукцию (нагрузку). Проблема может быть разбита на две части.
- Как мы должны распределить их по секторам, учитывая, что доступно ограниченное количество ресурсов?
- Сколько всего ресурсов должно быть распределено?
Эти принципы применимы вообще для любого вида производства. В нашем случае ресурсы соответствуют кабелям и оборудованию коммутации, а продукция состоит в обслуженной нагрузке. Сектор может быть линиями связи к станции. Проблема может состоять в определении линий связи между некоторой станцией и ее соседними станциями, с которым у нее есть прямые соединения. Тогда проблему можно сформулировать так:
- Сколько нагрузки нужно должна обслужить каждая линии связи, когда известно общее фиксированное количество нагрузки, которую надо обслужить?
- Сколько нагрузки нужно обслужить всего?
Вопрос 1 решен в секции 11.7.1, а вопрос 2 - в секции 11.7.2. Мы осуществляем дифференцирование для непрерывных переменных, потому что это проще. Подобное дифференцирование может быть сделано для дискретных переменных, соответствующих множеству каналов.
Этот принцип Мо рассмотрен в (Jensen, 1950 [50] ).
Балансирование предельных затрат
Пусть данная станция имеет прямые подключения к  другим станциям. Предположим, что стоимость подключения к станции
другим станциям. Предположим, что стоимость подключения к станции  , линейная функция от числа каналов:
, линейная функция от числа каналов:
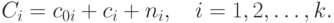 |
( 11.5) |
Общая стоимость кабелей тогда равна:
 |
( 11.6) |
где  - константа.
- константа.
Полная обслуженная нагрузка есть функция числа каналов:
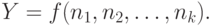 |
( 11.7) |
Если мы работаем с ограниченными ресурсами, то получим:
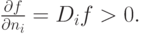 |
( 11.8) |
B системе с явными потерями 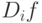 соответствует функции увеличения, которая является всегда положительной для конечного числа каналов из-за выпуклости B-формулы Эрланга.
соответствует функции увеличения, которая является всегда положительной для конечного числа каналов из-за выпуклости B-формулы Эрланга.
Мы хотим минимизировать  для данной полной обслуженной нагрузки
для данной полной обслуженной нагрузки  :
:
 |
( 11.9) |
Применяя множитель Лагранжа 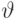 , где мы вводим
, где мы вводим 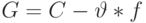 , получим эквивалентность:
, получим эквивалентность:
![min\{G(n_1, n_2, \dots, n_k)\}=min\{C(n_1, n_2, \dots, n_k)-\vartheta [f(n_1, n_2, \dots, n_k)-Y]\}](/sites/default/files/tex_cache/8e891f59e62fc133287bb73b4d331842.png) |
( 11.10) |
Необходимое условие для нахождения минимума:
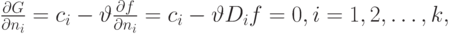 |
( 11.11) |
или
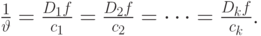 |
( 11.12) |
Таким образом, необходимым условием оптимального решения является то, что отношение роста обслуженной нагрузки при увеличении числа каналов (функции увеличения) к стоимости канала должно быть одинаковым для всех групп пучков каналов (7.33).
Установить набор необходимых и достаточных условий можно с помощью производных второго порядка, что и сделано в Принципе Мо (Jensen, 1950 [50]). Функции увеличения, с которыми мы работаем, будут всегда выполнять эти условия. Если мы также имеем различные доходы gдля отдельных групп пучков каналов (направлений), то должны ввести дополнительный коэффициент веса и заменить (11.12)  на
на 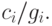
Оптимальная обслуженная нагрузка
Рассмотрим случай, когда обслуженная нагрузка является функцией числа каналов (11.7) -  . Если мы обозначаем доход
. Если мы обозначаем доход 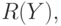 а затраты
а затраты 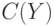 (11.6), то прибыль равна:
(11.6), то прибыль равна:
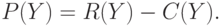 |
( 11.13) |
Необходимое условие оптимальной прибыли:
 |
( 11.14) |
то есть предельный доход должен быть равен предельным затратам.
Применяя
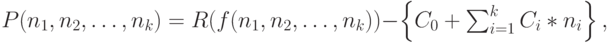 |
( 11.15) |
получаем оптимальное решение
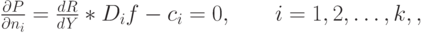 |
( 11.16) |
которое при использовании (11.12) дает
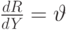 |
( 11.17) |
Коэффициент, 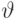 данный в (11.12) - отношение между стоимостью одного канала и нагрузки, которую можно обслужить дополнительно, если соединение будет увеличено на один канал. Таким образом, мы будем добавлять каналы к соединению, пока предельный доход не будет равен предельной стоимости
данный в (11.12) - отношение между стоимостью одного канала и нагрузки, которую можно обслужить дополнительно, если соединение будет увеличено на один канал. Таким образом, мы будем добавлять каналы к соединению, пока предельный доход не будет равен предельной стоимости 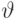 (7.35).
(7.35).
Пример 11.7.1: Оптимальное распределение емкости
Мы рассматриваем два направления (две группы пучков каналов), где предложенная нагрузка - 3 Эрл. и соответственно 15 Эрл. Каналы для этих двух систем имеют одну и ту же стоимость, общее количество доступных каналов - 25. Как мы должны распределить эти 25 каналов среди двух направлений?
Из (11.12) мы замечаем, что функции увеличения должны иметь приблизительно одинаковые значения для этих двух направлений. Поэтому проводим вычисления, используя таблицу:
Для 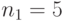 и
и 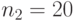 мы используем все 25 каналов. Это кончается перегрузкой 11.0 %, соответственно 4.6 %, то есть отмечается более высокая перегрузка для меньшей группы пучка каналов.
мы используем все 25 каналов. Это кончается перегрузкой 11.0 %, соответственно 4.6 %, то есть отмечается более высокая перегрузка для меньшей группы пучка каналов.
Пример 11.7.2: Оптимизация треугольника
Это классическая оптимизация сети треугольника используемой при альтернативной маршрутизации нагрузки (рис. 11.1). От A до B мы имеем запрос нагрузки, равный A Эрл. Нагрузку частично обслуживает на прямой маршрут (первичный маршрут) от A до B и частично - альтернативный маршрут (вторичный маршрут) 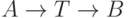 , где
, где  - транзитная станция. Другие возможности маршрутизации не используются. Стоимость прямого подключения -
- транзитная станция. Другие возможности маршрутизации не используются. Стоимость прямого подключения - 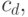 и для вторичного подключения -
и для вторичного подключения - 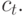
Сколько нагрузки нужно обслужить в каждом из этих двух направлений? Маршрут 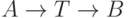 уже обслуживает нагрузку "к и от" других пунктов назначения, и мы обозначаем, предельное использование для канала на этом маршруте
уже обслуживает нагрузку "к и от" других пунктов назначения, и мы обозначаем, предельное использование для канала на этом маршруте  . Мы предполагаем независимость дополнительной нагрузки, которая поступит на обходной маршрут в результате блокировки от
. Мы предполагаем независимость дополнительной нагрузки, которая поступит на обходной маршрут в результате блокировки от 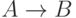 .
.
Согласно (11.12), условия минимума равны:
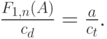
Здесь  - число каналов первичного маршрута. Это означает, что затраты должны быть одинаковыми как при обслуживании вызовов через прямой маршрут, так и через альтернативный маршрут.
- число каналов первичного маршрута. Это означает, что затраты должны быть одинаковыми как при обслуживании вызовов через прямой маршрут, так и через альтернативный маршрут.
Если бы один маршрут был дешевле другого, то мы направляли бы больше нагрузки в более дешевом направлении.
Так как нагрузки, которые мы применяем как основание для планирования, получаются путем измерения, они обычно характеризуются ненадежностью из-за ограниченной выборки, ограниченного периода измерений, принципа измерения и т.д. Как показано в Лекции 15, эта ненадежность приблизительно пропорциональна измеренному объему нагрузок. Измеряя за один и тот же период времени нагрузку для всех направлений, мы получим самую высокую неопределенность для маленьких по ёмкости направлений (групп пучков каналов), но она частично компенсируется вышеупомянутой чувствительностью к блокировкам, которая является наименьшей для маленьких групп пучков каналов. Как типичное представительское значение мы выбираем измеренную среднюю величину плюс стандартное отклонение, умноженное на константу, например, 1,0.
Мы должны быть уверены, и это должно далее быть подчеркнуто, что планируем сеть для обслуживания нагрузки в течение 1-2 лет от момента планирования. Поэтом значение, используемое для планирования, дополнительно имеет неопределенность прогноза. Мы не рассмотрели факт, что некоторая часть оборудования может не работать из-за технических ошибок.
ITU-T рекомендует, чтобы нагрузка для планирования была измерена в течение всех часов наибольшей нагрузки в течение года. Мы выбираем  , используя среднюю величину 5 наибольших наблюдений из 30 наибольших, чтобы получить следующие вероятности блокировки:
, используя среднюю величину 5 наибольших наблюдений из 30 наибольших, чтобы получить следующие вероятности блокировки:
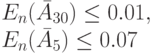 |
( 11.18) |
Вышеупомянутые критерии обслуживания могут быть непосредственно применены к отдельным группам пучков каналов. Практически, мы стремимся к заданной вероятности блокировки от A-абонента кB-абоненту, которая должна быть одинаковой для всех типов вызовов. При программном управлении станциями тенденция состоит в том, чтобы обеспечить непрерывную диспетчеризацию нагрузки на всех дорогих и международных маршрутах.
В заключение мы можем сказать, что значения нагрузки, используемое для планирования, имеет неопределенность, которая в большом пучке каналов суммируется. В некоторых приложениях непредвиденное значение нагрузки может кончиться серьезными последствиями для уровня обслуживания. В течение последних лет, наблюдается повышенный интерес к программам адаптации нагрузки и управления маршрутизацией (управление нагрузкой сети ), которые могут быть введены в программное управление цифровых систем телекоммуникаций. С помощью таких технологий мы можем в принципе выбирать оптимальную стратегию маршрутизации нагрузки при возникновении любого сценария.
Краткие итоги
- Планирование сети включает в себя проектирование, оптимизацию и поддержку функционирования телекоммуникационных сетей.
- Для того чтобы определить нагрузку в заданной области с
 станциями, мы должны знать значения
станциями, мы должны знать значения  нагрузки (
нагрузки ( 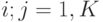 ), как это дано в матрице нагрузки. Матрица нагрузки предполагает, что мы знаем зоны нахождения станций.
), как это дано в матрице нагрузки. Матрица нагрузки предполагает, что мы знаем зоны нахождения станций. - Матрица нагрузки позволяет выбрать топологию сети и принцип маршрутизации нагрузки.
- Посредством метода двойных коэффициентов Круитофа мы можем оценить отдельные будущие значения
 матрицы нагрузки. Этот прогноз нагрузки может быть получен из абонентских прогнозов на отдельные станции.
матрицы нагрузки. Этот прогноз нагрузки может быть получен из абонентских прогнозов на отдельные станции. -
Если предположить, что линии связи на сети обслуживаются независимо, то вероятность блокировки из "конца в конец" вычисляется по классической формуле

Для малых вероятностей блокировки мы имеем:
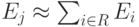 .
. - В телекоммуникационных сетях со многими пользователями, конкурирующими за одни и те же ресурсы (многостанционный доступ), важно определить сервисные требования пользователей и гарантировать, что при нормальных сервисных условиях будет гарантирован класс обслуживания (GoS).
- В системах (станциях) с программным управлением мы можем применять введение промежутков между вызовами ( call-gapping ) и распределение приоритетов для задач.
- Принцип Мо состоит в том, что оптимальное распределение ресурса получается при одновременном балансе предельных доходов и предельных затрат по всем секторам.