НОУ ИНТУИТ | Разработка телетрафика и планирование сетей. Лекция 9: Полнодоступные системы с потерями

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2011 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Пример 8.5.2: Ограниченное число источников

Можно оценить влияние ограничения числа источников, рассматривая либо потери по времени, либо потери по вызовам, либо потери по нагрузке. Значения потерь показаны на рис. 8.6 для фиксированного числа каналов я, фиксированной предложенной нагрузки А и увеличивающегося значения пиковости Z, соответствующего множеству источников S, который определяется как S=A/(1-Z) (8.23).

Предложенная нагрузка определяется как нагрузка, которую можно обслужить в системе при отсутствии блокировки ( п=1 ). Здесь

Z=1 соответствует Пуассоновскому потоку вызовов (В-формула Эрланга, Е=В=С ). Для Z< 1 мы получаем модель Энгсета, и для этого случая потери по времени Е являются больше, чем потери по вызовам В которые, в свою очередь, являются больше, чем потери по нагрузке С. Для Z>1 мы получаем модель Паскаля (секции 8.6 и 8.7 и пример 8.7.1).

Распределение Паскаля (отрицательное биноминальное распределение)

В Биноминальной модели интенсивность прибытия уменьшается линейно с увеличивающимся числом занятых источников. Пальма и Вальстром ввели модель, где интенсивность прибытия увеличивается линейно с числом занятых источников (Wallstrom, 1964 [100]). Интенсивность прибытия в состоянии i равна:

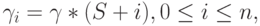$\gamma_i=\gamma*(S+i), 0 \le i \le n,$

( 8.59)

где $\gamma$ и S - положительные константы. Время пребывания в системе все еще принимается экспоненциально распределенным с интенсивностью $\mu$ .

В этой секции примем, что число каналов бесконечно. Мы составляем диаграмму переходов состояний (рис. 8.5 с п равным бесконечности) и находим устойчивые вероятности состояния, которые существуют только для 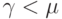$\gamma < \mu$ .

Мы получаем вероятности состояния:

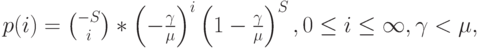$p(i)={-S\choose i}*\left (-\frac {\gamma}{\mu} \right )^i \left (1-\frac{\gamma}{\mu} \right )^S, 0 \le i \le \infty, \gamma < \mu,$

( 8.60)

где

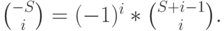${-S\choose i}=(-1)^i*{S+i-1\choose i}.$

( 8.61)

Формула (8.60) - отрицательное биноминальное распределение, также называемое распределением Паскаля (Таблица 6.1). Характеристики нагрузки этой модели получены соответствующей подстановкой параметров биноминального распределения. С этим распределением мы встретимся в следующей секции, которая имеет дело с более реальным случаем.

Усеченное распределение Паскаля

Мы рассматриваем тот же самый процесс и тип нагрузки, как в секции 8.6, но теперь ограничим число обслуживающих приборов конечным числом п. Ограничение 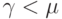$\gamma < \mu$ более не нужно, так как мы всегда будем получать статистическое равновесие с конечным числом состояний. Диаграмма переходов состояний показана на рис. 8.5, и вероятности состояния равны:

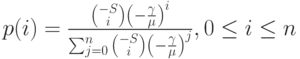$p(i)=\frac{{-S\choose i} \left (-\frac{\gamma}{\mu}\right )^i}{\sum_{j=0}^n{-S\choose i} \left (-\frac{\gamma}{\mu} \right )^j}, 0 \le i \le n$

( 8.62)

Это усеченное отрицательное биноминальное распределение (Паскалевское). Формально оно получено из Бернулли/Энгсета с использованием следующих подстановок:

$S \mbox{ заменено на } (-S)$

( 8.63)

$\gamma \mbox{ заменено на } (-\gamma)$

( 8.64)

С этими подстановками все формулы модели Бернулли/Энгсета справедливы для усеченного распределения Паскаля, и для числовой оценки могут быть использованы те же самые компьютерные программы.

Можно показать, что вероятности состояния (8.62), подобно вероятностям состояния для систем с потерями Эрланга и Энгсета, справедливы для произвольного распределения времени пребывания в системе (Iversen, 1980 [38]).

Если принять экспоненциально распределенные времена пребывания в системе, эта модель имеет те же самые вероятности состояния как первая нормальная форма Пальма. То есть система с Пуассоновским потоком вызовов имеет случайно распределенную интенсивность, как и гамма-распределение (интервалы поступления) становится распределенным по Парето. Такое распределение является медленно убывающим распределением. Эта модель используется для того, чтобы моделировать потерянную нагрузку, которая имеет пиковость больше единицы. Таким образом, мы получаем из (8.21) с помощью вышеупомянутой подстановки (8.64):

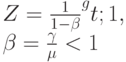$Z=\frac{1}{1- \beta} ^gt; 1, \\ \beta=\frac{\gamma}{\mu} < 1$

( 8.65)

Это усеченное отрицательное биноминальное распределение (Паскалевское). Напомним, что формально пиковость потока нагрузки вычисляется для бесконечного числа каналов. Для модели Паскаля мы получаем (см. (8.49)):

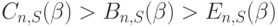$C_{n,S}(\beta) > B_{n,S}(\beta) > E_{n,S}(\beta)$

( 8.66)

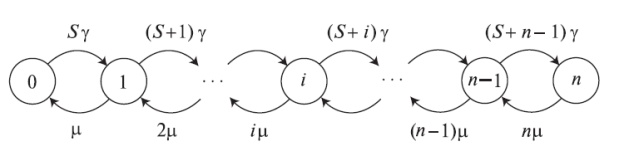
Рис. 8.5 . Диаграмма переходов состояний для модели Паскаля (усеченная отрицательная биноминальная модель)

Пример 8.7.1: Пиковость: числовой пример

На рис.8.6 мы принимаем число каналов n и при фиксированной предложенной нагрузке вычисляем вероятности блокировки, чтобы увеличить пиковость Z. Для Z>1 мы получаем модель Паскаля. Для этого случая потери по времени Е - меньше, чем потери по вызовам В, которые, в свою очередь, меньше, чем потери по нагрузке С.

Мы видим, что потери по времени и потери по вызовам имеют максимальное значение. Только потери по нагрузке дает разумное описание рабочих характеристик системы.

Пример 8.7.2: система с потерями Паскаля

Рассмотрим систему с потерями Паскаля с n=4 каналами и S=2 источниками. Интенсивность поступления 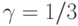$\gamma=1/3$ вызовов/ в единицу времени на свободный источник, и среднее время пребывания в системе 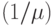$(1/\mu)$ - одна (1) единица времени. Мы находим следующие параметры для модели Энгсета, предположив, что S=-2 (8.63) и = -1/3 (8.64):

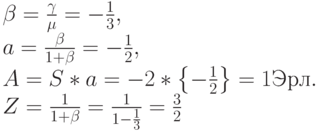
$\beta =\frac{\gamma}{\mu}=-\frac 13,\\ a=\frac{\beta}{1+\beta}=-\frac 12,\\ A=S*a=-2*\left \{ -\frac 12 \right \}=1 Эрл.\\ Z=\frac{1}{1+\beta}=\frac{1}{1-\frac 13}=\frac 32$

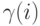	$\gamma(i)$	$\mu(i)$				$\gamma(i)*p(i)$
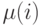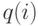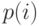0	0.6667	0	1.0000	0.4525	0.0000	0.3017
1	1.0000	1	0.6667	0.3017	0.3017	0.3017
2	1.3333	2	0.3333	0.1508	0.3017	0.2011
3	1.6667	3	0.1481	0.0670	0.2011	0.1117
4	2.0000	4	0.0617	0.0279	0.1117	0.0559
Total			2.2099	1.0000	0.9162	0.9721

Из диаграммы переходов состояний мы получаем следующие параметры:

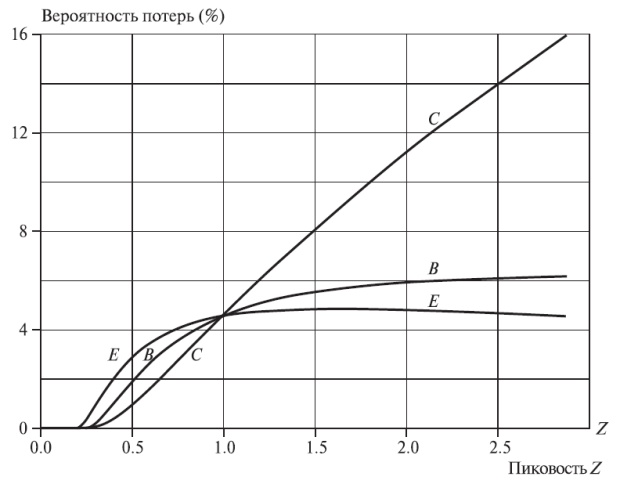
Потери по времени Е, потери по вызовам В и потери по нагрузке С как функция пиковости Z для РРР-нагрузки в системе с я=20 пучками каналов и предложенной нагрузкой =15 Эрл. Подробные комментарии даются в примерах 8.5.2 и 8.7.1. Для приложений самой важной характеристикой являются потери по нагрузке С, так как это почти линейная функция пиковости

Рис. 8.6. Потери по времени Е, потери по вызовам В и потери по нагрузке С как функция пиковости Z для РРР-нагрузки в системе с я=20 пучками каналов и предложенной нагрузкой =15 Эрл. Подробные комментарии даются в примерах 8.5.2 и 8.7.1. Для приложений самой важной характеристикой являются потери по нагрузке С, так как это почти линейная функция пиковости

Мы находим следующие вероятности блокировки.

Потери по времени:

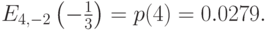
$E_{4,-2}\left ( - \frac 13 \right )=p(4)=0.0279.$

Потери по нагрузке:

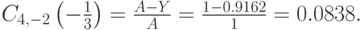
$C_{4,-2} \left (-\frac 13 \right )=\frac{A-Y}{A}=\frac{1-0.9162}{1}=0.0838.$

Потери по вызовам:

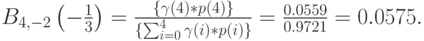
$B_{4,-2} \left ( -\frac 13 \right)=\frac{\{\gamma (4)*p(4)\}}{\{\sum_{i=0}^4 \gamma(i)*p(i)\}}=\frac{0.0559}{0.9721}=0.0575.$

Заметим, что Е<В<С является общим результатом для случая Паскаля. Используя для этого случая рекурсивную формулу для модели Энгсета случая (8.50), мы получаем те же самые результаты:

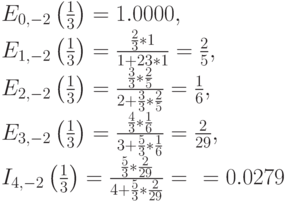
$E_{0,-2}\left( \frac 13 \right)=1.0000,\\ E_{1,-2}\left( \frac 13 \right)=\frac{\frac 23 *1}{1+ \farc 23 *1}=\frac 25,\\ E_{2,-2}\left( \frac 13 \right)=\frac{\frac 33 * \frac 25}{2+ \frac 33 *\frac 25}=\frac 16,\\ E_{3,-2}\left( \frac 13 \right)=\frac{\frac 43*\frac 16}{3+ \frac 53*\frac 16}=\frac{2}{29},\\ I_{4,-2}\left( \frac 13 \right)=\frac{\frac 53*\frac{2}{29}}{4+\frac 53*\frac{2}{29}}=\frac{}{}=0.0279$

Краткие итоги

В этой лекции обобщается классическая система с потерями Эрланга, Пуассоновским процессом поступления заявок, зависящих от состояния, которые обрабатывают так называемые модели ВРР-нагрузки ( ВРР - binomial, Poisson, Pascal).
Биноминальный случай характеризуется тем, что число источников S (абонентов, клиентов, заявителей) ограничено, а число каналов п всегда достаточно ( $S \le n$ ).
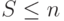В усеченном биноминальном распределении, которое также называется Распределением Энгсета, применяется ограниченное количество каналов, меньшее, чем число источников ( n < S ).
Рассматриваем систему со структурой "полнодоступная группа" и стратегией, в которой "потерянный вызов покидает систему без влияния на дальнейшие процессы". Далее мы предполагаем, что времена обслуживания являются экспоненциально распределенными с интенсивностью $\mu$ (средняя величина $1/\mu$ ,)
Для модели Энегсета и для модели Паскаля предложенная нагрузка определяется как нагрузка, которую может обслужить неограниченное число обслуживающих приборов.
Пиковость определяется как отношение между дисперсией и средней величиной вероятностей состояния. Для предложенной нагрузки пиковость рассматривается для бесконечного числа каналов.
Модель Энегсета (B-Биноминальная модель) рассматривает ограниченное число источников S. Отдельный источник имеет постоянную интенсивность поступления вызовов (прибытие), когда он свободен. Когда он занят, интенсивность вызовов рана нулю.
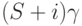Модель Палъма-Волъстрема (Р-модель Паскаля): рассматривает ограниченное число источников S. Если в данный момент мы имеем / занятых источников, то интенсивность прибытия равняется $(S+i)\gamma$ .
Биноминальное распределение определяется выражением:

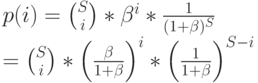
$p(i)={S\choose i}*\beta^i*\frac{1}{(1+\beta)^S}\\ ={S\choose i}* \left( \frac{\beta}{1+\beta} \right)^i* \left ( \frac{1}{1+\beta} \right)^{S-i}$
Вероятности состояния модели Энгсета:

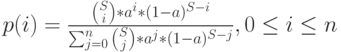
$p(i)=\frac{{S\choose i}*a^i*(1-a)^{S-i}}{\sum_{j=0}^n {S\choose j}*a^j*(1-a)^{S-j}}, 0 \le i \le n$
Потери по времени Е, по определению, пропорциональны времени, когда система заблокирована для новых попыток вызова:

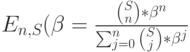
$E_{n,S}(\beta}=\frac{{S\choose n}*\beta^n}{\sum_{j=0}^n {S\choose j}*\beta^j}$
Потери по вызовам В, по определению, пропорциональны числу потерянных попыток вызова:

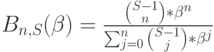
$B_{n,S}(\beta)=\frac{{S-1\choose n}*\beta^n}{\sum_{j=0}^n {S-1\choose j}* \beta^j}$
Потери по нагрузке выражаются следующей формулой:

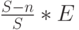
$\frac{S-n}{S}*E$
Обслуженная нагрузка на один источник выражается следующей формулой:

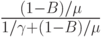
$\frac{(1-B)/\mu}{1/ \gamma +(1-B)/\mu}$
Полная обслуженная нагрузка выражается следующей формулой:

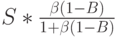
$S*\frac{\beta (1-B)}{1+ \beta (1-B)}$
Число попыток вызова в единицу времени:

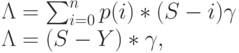
$\Lambda = \sum_{i=0}^n p(i)*(S-i) \gamma\\ \Lambda = (S-Y)* \gamma,$
где Y - обслуженная нагрузка.
Потерянная нагрузка:

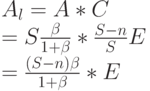
$A_l=A*C\\ =S \frac{\beta}{1+\beta}*\frac{S-n}{S}E\\ =\frac{(S-n) \beta}{1+ \beta}*E$
Пальма и Вальстром ввели модель, где интенсивность прибытия увеличивается линейно с числом занятых источников (Wallstrom, 1964 [100]). Интенсивность прибытия в состоянии равна:

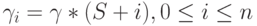
$\gamma_i=\gamma * (S+i), 0 \le i \le n$
и
Усеченное отрицательное биноминальное распределение (Паскалевское):

$p(i)=\frac{{-S\choose i}\left ( -\frac{\gamma}{\mu}\right )^i}{\sum_{j=0}^n {-S\choose j} \left ( -\frac{\gamma}{\mu} \right )^j}, 0 \le i \le n$