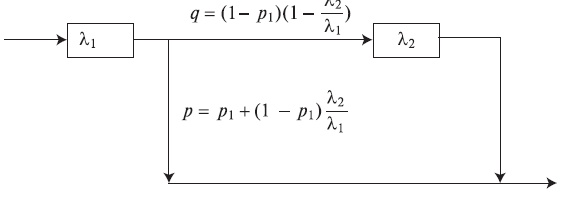НОУ ИНТУИТ | Разработка телетрафика и планирование сетей. Лекция 5: Распределение моментов поступления вызовов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 20.04.2011 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Принципы декомпозиции

Диаграммы состояния - полезный инструмент для того, чтобы анализировать Распределения Кокса. Ниже приводится фундаментальная характеристика экспоненциального распределения (Iversen и Nielsen, 1985 [41]).

Теорема 4.1. Экспоненциальное распределение с интенсивностью $\lambda$ может быть представлено как два фазовых распределения Кокса, где первая фаза имеет интенсивность $\mu > \lambda$ и вторая - фазовую интенсивность $\lambda$ (сравните с рис.4.8).

Согласно Теореме 4.1 гиперэкспоненциальное распределение с 'l фазами эквивалентно распределению Кокса с тем же самым числом фаз. Случай l = 2 показан на рис.4.10.

Другое свойство распределений Кокса (Iversen и Nielsen, 1985 [41]):

Теорема 4.2. Фазы в любом Распределении Кокса можно упорядочить как $\lambda \ge \lambda_{+1}$ .

Теорема 4.1 показывает, что экспоненциальное распределение эквивалентно гомогенному распределению Кокса (здесь "гомогенное" означает "имеет одну и ту же интенсивность во всех фазах") с интенсивностью m и бесконечное число фаз (рис.4.8). Заметим, что переходные вероятности постоянны.

Pис.4.9 показывает взвешенную сумму k распределений Эрланга, где весовые коэффициенты распределены геометрически.

Рис. 4.8.

Экспоненциальное распределение с коэффициентом /lambda эквивалентно показанному распределению Кокса (Теорема 4.1)

Рис. 4.9.

Экспоненциальное распределение с коэффициентом /lambda может быть декомпозировано с помощью последовательного разложения в составное распределение гомогенных k распределений Эрланга с коэффициентом $\mu > \lambda$ , где весовые коэффициенты геометрически распределены (частное $p=\lambda / \mu$ ).

Используя диаграммы состояния, просто показать, что любой экспоненциальный временной интервал $(\lambda)$ может быть разложен на распределения фазового типа $(\lambda_i)$ , где $\lambda_i \ge \lambda$ . Что касается рис.4.11, мы заметим, что интенсивность макросостояния (обведенный штриховой линией блок) $\lambda$ независима от микросостояния.

Рис. 4.10.

Гиперэкспоненциальное распределение с двумя фазами ( $\lambda_1 > \lambda_2, p_2=1-p_1$ ) может быть преобразовано в распределение Кокса 2 (сравните с рис.4.4)

Когда число фаз k конечно и нет обратной связи, конечная фаза должна иметь интенсивность $\lambda$ .

Рис. 4.11.

Это распределение фазового типа эквивалентно единственному экспоненциальному распределению. Когда $p_i* \lambda_i=\lambda$ . Соответственно $\lambda_i \ge \lambda$ и $0 < p_i \le 1$ .

Важность Распределения Кокса

В последние годы распределения Кокса привлекли к себе большое внимание, поскольку они обладают следующими свойствами:

распределение Кокса может быть проанализировано с использованием метода фаз;
для произвольного распределения можно найти хорошее приближение к распределению Кокса. Свойство, справедливое для распределения Кокса, справедливо для любого распределения, имеющего практический интерес.

Используя Распределения Кокса, мы можем элементарными методами получать результаты, которые раньше требовали очень сложной математики.

В практических приложениях теории мы использовали распределения Кокса для получения методов оценки параметров. При решении статистической проблемы есть 2k параметра. Обычно мы можем выбрать специальное распределение Кокса (например, k - распределение Эрланга или гиперэкспоненциальное распределение) и приблизительный первый момент.

Применяя метод рулетки, мы с помощью числового моделирования на компьютерах автоматически получаем результаты наблюдений временных интервалов в виде распределения Кокса с одной и той же интенсивностью для всех фаз.

Другие распределения времени

В принципе, каждое распределение, которое не имеет отрицательных значений, может использоваться как распределение времени и описывать временные интервалы. Но, практически, прежде всего востребованы вышеупомянутые распределения.

Мы предполагаем, что параметр k -распределении Эрланга (4.8) принимает неотрицательные реальные значения, и получаем гамма- распределение:

$f(t)=\frac{1}{\Gamma(k)}(\lambda t)^{k-1}*e^{-\lambda t}*\lambda, \lambda > 0, t \ge 0.$

( 4.39)

Средняя величина и дисперсия даются в (4.11) и (4.12). Это распределение также известно в теории телетрафика как Распределение Вейбулла.

Оно дает зависимость интенсивности времени отказа (3.14):

$\frac{dF(t)}{1-F(t)}=\mu(t)=\frac{\lambda e^{-(\lambda t)^k}*k(\lambda t)^{k-1} dt}{e^{-(\lambda t)^k}}\\ \qquad \qquad=\lambda k(\lambda t)^{k-1}.$

( 4.41)

Распределение применяется в теории надежности. Для k=1 мы имеем экспоненциальное распределение. Распределение Парето получается:

$F(t)=1-(1+\eta_0t)^{-(1=\frac{\lambda}{\eta_0})}.$

( 4.42)

Средняя величина и коэффициент формы следующие:

$m_1=\frac{1}{\lambda},\\ \varepsilon=\frac{2\lambda}{\lambda - \eta_0}, 0 < \eta_0 < \lambda.$

( 4.43)

Надо обратить внимание, что для $\lambda \le \eta_0$ дисперсия не существует. Если $\eta_0 \to 0$ (4.42), распределение становится экспоненциальным. Если интенсивность Пуассоновского процесса - гамма-распределеление, то времена между прибытиями распределены, согласно Парето.

Далее мы будем иметь дело с набором дискретных распределений, которые также описывают время жизни - такие, как геометрическое распределение, распределение Паскаля, Биноминальное распределение, распределение Вестенберга и т.д. На практике параметры распределений не всегда постоянны.

Время обслуживание (удержания) может быть физически коррелированным с состоянием системы. В системах человек/машина время обслуживания изменяется из-за занятости (уменьшается) или усталости (увеличивается). Электромеханические системы работают более медленно в течение периодов высокой нагрузки, потому что в это время наблюдается уменьшение напряжения электрической сети.

Для некоторых распределений, которые широко применяются в теории организации очереди, мы используем следующую систему сокращенных обозначений (сравните с секцией 13.1):

М - экспоненциальное (марковское) распределение,

E_k - k -распределение Эрланга,

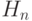H_n - гиперэкспоненциальное распределение порядка n,

D - (детерминированная) константа,

Сох - распределение Кокса,

G - общий - произвольное распределение.

Наблюдения распределения времени жизни

Pис.4.5 показывает пример наблюдаемых времен пребывания в системе местной телефонной станции. Время пребывания в системе состоит из времени сигнализации и в случае, если появляется ответ, дополняется время сеанса связи.

Pис.4.2 показывает наблюдаемые времена между прибытиями входящих вызовов на транзитную телефонную станцию в течение одного часа.

С самого начала для теории телетрафика было характерно сильное взаимодействие с практикой, и были превосходные возможности проводить измерения.

Эрланг (1920, [11]) и звещает об измерениях, при которых был зарегистрирован 2461 сеанс связи на телефонной станции в Копенгагене.

Пальм (1943 [79]) и теоретически и фактически анализировал измерения нагрузки. Он проводил объемные измерения в Швеции.

При помощи компьютерной технологии может быть собрано большое количество данных. Первая программа, управляющая компьютерным измерением, описана в (Iversen, 1973 [35]). Важность использования дискретных значений времени при наблюдении значений показано в Лекции 15.

В. Болотин (1994, [7]) измерил и моделировал времена пребывания в телекоммуникационной системе.

Многочисленные измерения были проведены на компьютерных системах. В телефонных системах мы редко имеем коэффициенты формы больше, чем 6, При измерении нагрузки передачи данных наблюдаются коэффициенты формы больше, чем 100. Так обстоит дело, например, при передаче данных, когда мы передаем либо несколько символов, либо большое количество данных. Чтобы описать эти данные, используются медленно убывающие распределения. Медленно сходящиеся распределения в строгом смысле - это функция, остаток распределения которой ведет себя согласно степенному закону, то есть

$1-F(t) \approx t^{-\alpha}, 0 < \alpha \le 2.$

Распределение Парето (4.42) - медленно убывающее в строгом смысле. Иногда распределения, убывающие медленнее, чем экспоненциальное распределение, классифицируются как медленно убывающие: например, распределения гиперэкспоненциальное, Вейбулла, нормальное распределение.

В настоящее время выполнены большие измерения и проведено моделирование распределения, использующее самоподобные модели трафика (Jerkins & other,1999 [51]). С этими распределениями мы будем иметь дело в следующих лекциях.

Краткие итоги

Экспоненциальное распределение - самое важное распределение времени в теории телетрафика.
Экспоненциальное распределение имеет некоторые уникальные характеристики, которые делают возможным его аналитическое и практическое использование. Экспоненциальное распределение играет ключевую роль среди всех распределений времени "жизни".
Экспоненциальное распределение характеризуется единственным параметром: интенсивностью или скоростью $\lambda$ . Самая фундаментальная характеристика экспоненциального распределения - отсутствие памяти.
Распределение остатка времени соединения связи не зависит от фактической продолжительности этого соединения и равно распределению всего времени "жизни".
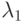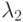Пусть две случайных переменные и являются взаимно независимыми и экспоненциально распределенными с интенсивностями $\lambda_1$ и $\lambda_2$ соответственно. Новая случайная переменная X определяется как:

$X+min\{X_1, X_2\}.$
Функция распределения X равна:

$p\{X \le t\}=1-e^{-(\lambda_1+\lambda_2)t}$ .
С помощью одного экспоненциального распределения (то есть одного параметра) мы не можем описать достаточно детально временные интервалы, поэтому придется использовать комбинацию двух или более экспоненциальных распределений.
Пальма ввел два класса распределений: крутое и плоское. Крутое распределение соответствует набору последовательных, стохастических независимых экспоненциальных распределений, а плоское - параллельным экспоненциальным распределениям.
Комбинируя крутое и плоское распределения, мы можем получить произвольно хорошее приближение для любой функции распределения.
Крутые распределения также называют гиперэкспоненциальными распределениями или обобщенными распределениями Эрланга с коэффициентом формы в интервале $1 \varepsilon \le 2$ .
Плоское распределение - это обобщенная функция распределения, полученная свертыванием k экспоненциальных распределений.
Гиперэкспоненциальные распределения могут быть получены комбинацией k параллельных экспоненциальных распределений, где вероятность выбора i -того распределения - .
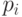Комбинируя крутые и плоские распределения, мы получаем общий класс распределений (распределения фазового типа) - распределения Кокса, которые могут быть описаны с помощью экспоненциальной фазы в последовательном и параллельном случае (например, $k \times l$ матрицей).
Если мы полагаем, что точка выбрана наугад в пределах временного интервала, подчиняющегося распределению Кокса, то вероятность, что эта точка - в пределах фазы , равна:

$\frac{m_i}{m}, i=1,2, \dots, k.$
Если мы повторяем этот эксперимент раз (независимо), то вероятность, что фаза наступала раз, определяется с помощью мулътино-мжального распределения (полиномиальное распределение).
Экспоненциальное распределение с интенсивностью $\lambda$ может быть представлено как два фазовых распределения Кокса, где первая фаза имеет интенсивность $\mu > \lambda$ и вторая - фазовую интенсивность $\lambda$ .