| Высшее образование |
Организация компьютерных экспериментов
7.3.6. Проведение экспериментов
Вначале проведите эксперимент согласно варианту 1 (см. п. 7.3.3 и рис. 7.14).
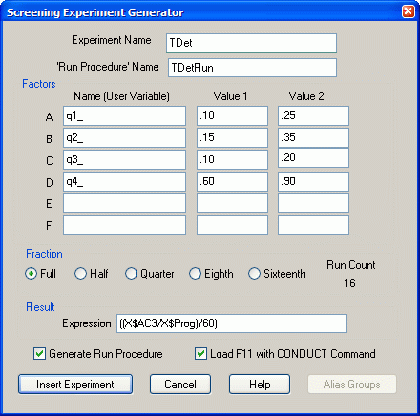
Рис. 7.14. Диалоговое окно (заполненное) Screening Experiment Generator (Генератор отсеивающего эксперимента)
Ранее (п. 4.9) отмечалось, что из трех подходов получения достоверной статистики наиболее удобен подход сброса статистики на определенном этапе моделирования с последующим его продолжением без модификации модели. Для реализации этого подхода в GPSS World имеется команда RESET.
Однако остается открытым вопрос: сколько нужно выполнить предварительных прогонов модели до сброса статистики?
Для получения ответа на этот вопрос проведите несколько экспериментов с моделью, меняя в каждом из них только количество предварительных прогонов модели.
В первой команде START генератора экспериментов укажите 20 прогонов. Во второй команде START - 170 прогонов, которые были определены ранее (п. 7.3.4). Результаты экспериментов - оценку матожидания времени TDet изготовления Det деталей - заносите в табл. 7.5.
| Оценка | Количество прогонов модели | ||||||
|---|---|---|---|---|---|---|---|
| 20 | 40 | 60 | 80 | 100 | 120 | 150 | |
| TDet | 3,988 | 3,975 | 4,007 | 4,024 | 3,986 | 3,995 | 4,044 |
Согласно табл. 7.5 изменяйте и количество прогонов модели. Для сокращения времени проведения экспериментов изменяйте их непосредственно в процедуре запуска генератора экспериментов.
По окончании экспериментов получите (табл. 7.5). Видно, что изменения результата моделирования столь малы, что ими для данной модели практически можно пренебречь.
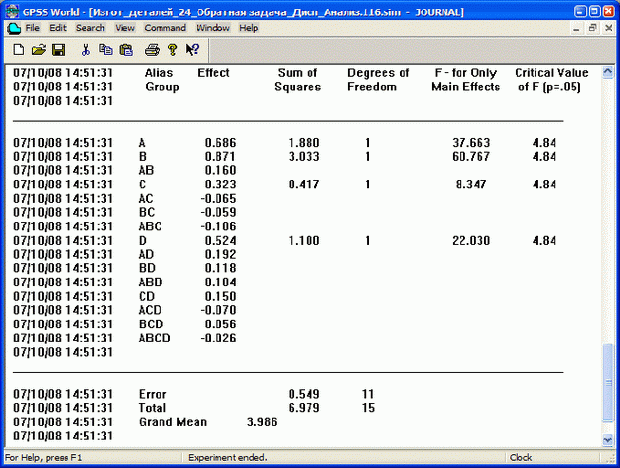
Повторите эксперимент, указав, например, 100 предварительных прогонов. Получите результаты дисперсионного анализа, представленные на рис. 7.15.
Видно, что все четыре фактора существенные. Наибольшее влияние на функцию отклика оказывает фактор В, что вполне логично, так как из первых трех имеет наибольший верхний уровень, т. е. наибольшую долю брака. Ожидаемое время изготовления четырех деталей DET = 4 деталей составляет ТDet = 3,986 ч.
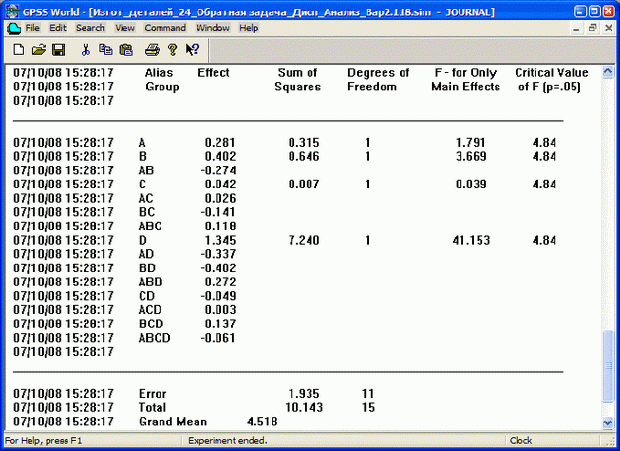
Теперь проведите эксперимент согласно варианту 2 (см. п. 7.3.3) при том же количестве предварительных и основных прогонов. Получите (рис. 7.16), что ожидаемое время изготовления четырех деталей ТDet = 4,518 ч. Все факторы, кроме фактора D (время выполнения третьей операции), несущественные.
Уменьшите верхний уровень фактора D: возьмем, например, K1 = 1,5. Проведите эксперимент с новым значением фактора D. Получите, что время изготовления ТDet ожидается 3,992 ч, а все факторы можно считать практически не существенными.
Вопросы для самоконтроля
- Что понимается под компьютерным экспериментом?
- Каковы цели стратегического и тактического планирования эксперимента?
- Какова цель и средства проведения дисперсионного анализа (отсеивающего эксперимента) в GPSS World?
- В каком виде выводятся результаты дисперсионного анализа? Дайте характеристику выводимых величин.
- Как изучить группы смешивания с целью осуществления стратегического планирования эксперимента?
- Какова цель и средства проведения оптимизирующего эксперимента в GPSS World?
- Дайте характеристику метода поверхности отклика.
- Как должны быть представлены в программе модели характеристики моделируемой системы, которые будут использоваться при проведении исследований с применением генераторов экспериментов?
- Можно ли при проведении отсеивающего или оптимизирующего эксперимента указывать, например, для нормального или равномерного распределения, по отдельности в качестве факторов среднее значение и среднеквадратическое отклонение? Если да, приведите примеры. Если нет, обоснуйте причину, к каким ошибкам это может приводить, как их избежать.
- Может ли пользователь изменять условия проведения отсеивающего и оптимизирующего экспериментов? Если да, какие?
- Измените условия примера 6.1 так, чтобы сервер стал однофазной системой массового обслуживания с ожиданием разомкнутого типа (добавьте входной накопитель емкостью на L сообщений). В соответствии с этим откорректируйте программу модели решения прямой задачи (п. 6.3.1). Проведите дисперсионный анализ. Исследуйте влияние на вероятность обработки запросов сервером четырех факторов: три указаны в табл. 6.1, а четвертый фактор - емкость входного накопителя сервера.
- В программу модели, измененную при ответе на вопрос 7.11, добавьте сегмент имитации сбоев сервера. Проведите дисперсионный анализ. Исследуйте влияние на вероятность обработки запросов сервером пяти факторов: четыре указаны в вопросе 7.11, а пятый фактор - среднее значение интервалов времени наработки на отказ.
- Проведите оптимизирующий эксперимент, используя те же факторы, что и в дисперсионном анализе (вопрос 7.11). Попробуйте получить регрессионную зависимость, изменяя, при необходимости, значения уровней факторов.
- Проведите оптимизирующий эксперимент согласно условиям варианта 1 (п. 6.4.1.3). Попробуйте получить регрессионную зависимость, изменяя, при необходимости, значения уровней факторов.
- Проведите оптимизирующий эксперимент согласно условиям варианта 2 (п. 6.4.1.3). Попробуйте получить регрессионную зависимость, изменяя, при необходимости, значения уровней факторов.
- Измените исходные данные задачи (п. 6.5.2): добавьте телефонные аппараты третьей категории (ТА3). Откорректируйте в соответствии с этим программу модели (п. 6.5.4). Проведите дисперсионный анализ. Исследуйте зависимость вероятностей разговоров абонентов ТА по категориям и в целом от интенсивности заявок на звонки и длительности ведения разговоров.
- Проведите оптимизирующий эксперимент по условиям вопроса 7.16. Попробуйте получить регрессионную зависимость, изменяя, при необходимости, значения уровней факторов.
- Проведите дисперсионный анализ согласно постановке п. 7.3.1. Но при этом решите прямую задачу, т. е. определите количество деталей, которое будет изготовлено за четыре часа. Для этого замените сегмент завершения моделирования и расчета результатов сегментом задания времени моделирования и расчета результатов:
GENERATE TMod ; Время моделирования TEST L X$Prog,TG1,Met11 ; Если условие выполняется, то SAVEVALUE Prog,TG1 ; X$Prog=TG1 содержимому счетчика завершений SAVEVALUE Prog1,TG1 ; X$Prog1=TG1 содержимому счетчика завершений Met11 TEST E TG1,1,Met12 ; Если содержимое счетчика завершений равно 1, то расчет результатов моделирования SAVEVALUE NDet,(INT(N$EndOper1/X$Prog1)) ; Количество готовых деталей, шт. SAVEVALUE Brak,(INT(N$EndOper/X$Prog1)) ; Количество забракованных деталей, шт. SAVEVALUE DoljaBrak,(X$Brak/(X$Brak+X$NDet)) ; Общая доля брака SAVEVALUE DoljaDet,(X$NDet/(X$Brak+X$NDet)) ; Доля готовых деталей SAVEVALUE TDet,((AC1-X$AC2)/N$EndOper1) ; Среднее время изготовления одной детали, мин SAVEVALUE AC2,AC1 SAVEVALUE Prog,0 Met12 TERMINATE 1
Остальную необходимую корректировку модели выполните самостоятельно.