| Высшее образование |
Организация компьютерных экспериментов
7.2. Регрессионный анализ (оптимизирующий эксперимент). Прямая задача
Дисперсионный анализ (отсеивающий эксперимент) показывает силу влияния каждого фактора на наблюдаемую переменную (отклик). Однако оптимизация и количественный прогноз поведения систем часто являются основными задачами моделирования. В GPSS World решение таких задач возможно посредством проведения регрессионного анализа (оптимизирующего эксперимента).
Оптимизация моделируемого процесса состоит в определении таких значения уровней факторов, при которых показатель эффективности процесса достигает максимального значения (или минимального - в зависимости от смысла показателя эффективности).
В общем случае показатель эффективности представляется уравнением регрессии
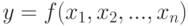
где 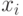 - значения уровней факторов процесса;
- значения уровней факторов процесса;  -количество управляемых факторов.
-количество управляемых факторов.
Оптимизация многофакторного, особенно нелинейного уравнения регрессии, задача не простая, и для ее решения разработан ряд численных методов. Наиболее эффективен при компьютерном моделировании так называемый метод поверхностей, при котором уравнение регрессии трактуется как уравнение поверхности в многофакторном пространстве. Оптимальное решение в этом случае составляют координаты из значений факторов вершины (или впадины) этой поверхности. Поиск оптимума осуществляется последовательными изменениями (шагами) значений уровней факторов в направлении, на котором обнаруживается улучшение показателя эффективности. Такой метод реализован в GPSS World.
Пользователь задает исходные условия, а GPSS World автоматически создает план и проводит с поверхностью отклика эксперимент, который отыскивает оптимальное значение. В ходе эксперимента GPSS World пытается подобрать либо линейную модель, либо модель второго порядка (включая двухфакторные взаимодействия).
Рассмотрим на примере проведение регрессионного анализа (оптимизирующего эксперимента).
Пример 7.2. В условиях примера 6.1 провести регрессионный анализ результатов моделирования. При этом вычислительную сложность обработки запросов сервером взять распределенной не по нормальному, а по экспоненциальному закону, т. е. в программе модели примера 6.1 удалить строку
S2_ EQU 200000 ; Стандартное отклонение вычислительной сложности запросов, оп
а строку с блоком ADVANCE заменить строкой:
ADVANCE ((Exponential(32,0,S_))/Q_) ; Имитация обработки запроса
Откройте модель примера 6.1. Сохраните как Reg_Server. Внесите рекомендованные изменения.
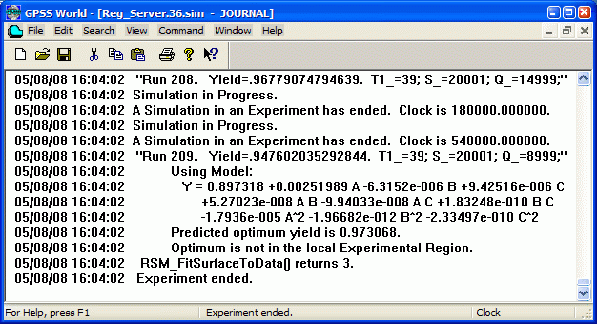
Выберите Edit / Insert Experiment / Optimising … ( Правка / вставить эксперимент / Оптимизирующий … ). Откроется диалоговое окно Optimizing Experiment Generator ( Генератор оптимизирующего эксперимента ).
Введите имена факторов и значения уровней (рис. 7.10).
В поле Expression ( Выражение ) группы Result ( Результат ) введите выражение, по которому рассчитывается результат наблюдения:
(N$ObrZap/N$KolZap)
Оптимизирующий эксперимент нужно ограничить пределами. Группа полей Movement ( Пределы перемещения ) позволяет ограничить перемещение локальной экспериментальной области. Если это возможно, необходимо ввести пределы изменения для каждого фактора эксперимента. Другой способ ограничить поиск - задание величины Redirection Limit ( Предел изменения направления ). Это значение устанавливает предел на количество изменений направления движения эксперимента по факторному пространству.
Введите в поля эти данные, приведенные на рис. 7.10.
Далее, так как вероятность обработки запросов должна быть максимальной, оставьте Maximize. Также установите флажки, позволяющие выбрать опции Generate Run Procedure и Load F12 with CONDUCT Command. Назначение этих опций такое же, как и в генераторе отсеивающего эксперимента. Только после создания объекта "Процесс моделирования" для запуска эксперимента нужно нажать функциональную клавишу [ F12 ], а не [ F11 ].
Все необходимые данные введены в соответствующие поля. Нажмите кнопку Insert Experiment ( Вставить эксперимент ). Так как GPSS World было указано сгенерировать процедуру запуска, то появится диалоговое окно, позволяющее отредактировать ее так же, как и в генераторе отсеивающего эксперимента. После корректировки нажмите Ok. Автоматически сгенерированные Plus-операторы появятся в нижней части модели.
Для запуска эксперимента сначала создайте, нажав [ Ctrl ]+[ Alt ]+[ S ], объект "Процесс моделирования". При успешном завершении появится соответствующее сообщение (рис. 7.11).
Рис. 7.11. Сообщение об успешном создании объекта "Процесс моделирования" для проведения регрессионного анализа
После такого сообщения нажмите функциональную клавишу [ F12 ]. Эксперимент начнет выполняться. В окно Journal ( Журнал ) процесса моделирования будут выводиться отчеты о состоянии и результатах каждого наблюдения.
По отчетам можно узнать о перемещении локальной экспериментальной области. Plus-эксперимент пытается переместить локальную экспериментальную область так, чтобы она включала в себя оптимальные условия. Если это происходит, или, если достигнут предел изменения направления или предел перемещения, эксперимент заканчивается.
Когда перемещение останавливается, в окно Journal ( Журнал ) также выводятся результаты проверки критерия адекватности и уравнение подобранной (найденной) поверхности отклика. Затем, если это еще не сделано, Plus-эксперимент пытается проверить прогнозируемые оптимальные условия, запустив процесс моделирования для них.
Результаты регрессионного анализа (оптимизирующего эксперимента), после 209 наблюдений, приведены на рис. 7.12.
Заметим, что это на 201 наблюдение больше, чем при проведении дисперсионного анализа (отсеивающего эксперимента) (п. 7.1). Оптимум не находится в локальной экспериментальной области.
Полученное уравнение поверхности отклика имеет вид:
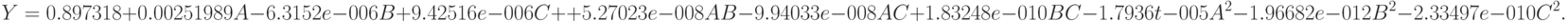
Оптимальное значение вероятности обработки запросов сервером составляет 0.973068.
При проведении оптимизирующего эксперимента важным является задание локальной экспериментальной области. Значения факторов, указанные исследователем, формируют начальную точку эксперимента. От этого зависит достижение его цели, заключающейся:
- в получении оптимального значения в пределах локальной области;
- выполнении подтверждающего прогона;
- выводе модели, которая была использована.
Следует иметь в виду, что цель получения математической модели в оптимизирующем эксперименте достигается не всегда.