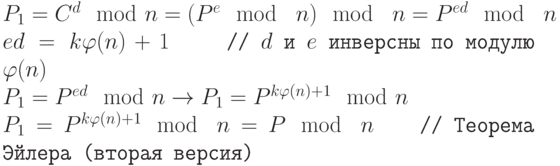| Экстернат |
Криптографическая система RSA
14.2. Криптографическая система RSA
Самый общий алгоритм открытого ключа доступа — криптографическая система RSА, названная по имени его изобретателей Ривеста, Шамира, Эделмана (Rivest, Shamir и Adelman).
Введение
RSА использует два типа ключей — e и d, где e — открытый, a d — секретный. Предположим, что P — исходный текст и C — зашифрованный текст. Алиса использует C = Pe mod n, чтобы создать зашифрованный текст C из исходного текста P ; Боб использует P = Cd mod n, чтобы извлечь исходный текст (файл), переданный Алисой. Модулей n создается очень большое количество с помощью процесса генерации ключей, который мы обсудим позже.
Для шифрования и дешифрования применяют возведение в степень по модулю. Как мы уже обсуждали в лекциях 12-13, при использовании быстрого алгоритма возведение в степень по модулю выполнимо в полиномиальное время. Однако нахождение модульного логарифма так же сложно, как и разложение числа по модулю. Для него нет алгоритма с полиномиальным временем. Это означает, что Алиса может зашифровать сообщение общедоступным ключом (e) в полиномиальное время. Боб также может расшифровать его в полиномиальное время (потому что он знает d ). Но Ева не может расшифровать это сообщение, потому что она должна была бы вычислить корень e -той степени из C с использованием модульной арифметики. Рисунок 14.5 показывает идею RSA.
Другими словами, Алиса использует одностороннюю функцию (возведение в степень по модулю) с лазейкой, известной только Бобу. Ева не знает лазейку, поэтому не может расшифровать сообщение. Если когда-нибудь найдут полиномиальный алгоритм для модуля вычисления корня e -той степени из n, то возведение в степень по модулю n не будет больше односторонней функцией.
Процедура
Рисунок 14.6 показывает общую идею процедуры, используемой в RSA.
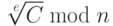
Две алгебраические структуры
RSA использует две алгебраических структуры: кольцо и группу.
Кольца шифрования/дешифрования. Шифрование и дешифрование сделаны с использованием коммутативного кольца  с двумя арифметическими операциями: сложение и умножение. В RSA это кольцо общедоступно, потому что модуль n общедоступен. Любой может послать сообщение Бобу, используя это кольцо для шифрования.
с двумя арифметическими операциями: сложение и умножение. В RSA это кольцо общедоступно, потому что модуль n общедоступен. Любой может послать сообщение Бобу, используя это кольцо для шифрования.
Группы генерирования ключей. RSA использует мультипликативную группу  для генерации ключей. Группа поддерживает только умножение и деление (мультипликативную инверсию), которые необходимы для того, чтобы создать открытые и секретные ключи. Эту группу надо скрыть, потому что ее модуль
для генерации ключей. Группа поддерживает только умножение и деление (мультипликативную инверсию), которые необходимы для того, чтобы создать открытые и секретные ключи. Эту группу надо скрыть, потому что ее модуль  является секретным. Мы увидим, что если Ева найдет этот модуль, она сможет легко атаковать криптографическую систему.
является секретным. Мы увидим, что если Ева найдет этот модуль, она сможет легко атаковать криптографическую систему.
 (n)* , x >.
(n)* , x >.Генерация ключей
Боб использует шаги, показанные в алгоритме 14.2, чтобы создать свои открытый и секретный ключи. После генерации ключей Боб объявляет кортеж (e, n) как свой открытый ключ доступа: Боб сохраняет d как свой секретный ключ. Боб может отказаться от p, q и  ; они не могут изменить его секретный ключ, не изменяя модуль. Для безопасности рекомендуется размер для каждого простого p или q — 512 бит (почти 154 десятичные цифры). Это определяет размер модуля, n 1024 бита ( 309 цифр).
; они не могут изменить его секретный ключ, не изменяя модуль. Для безопасности рекомендуется размер для каждого простого p или q — 512 бит (почти 154 десятичные цифры). Это определяет размер модуля, n 1024 бита ( 309 цифр).
14.2. RSA-генерация ключей
Шифрование
Передать сообщение Бобу может любой, используя его открытый ключ доступа. Шифрование в RSA может быть выполнено с использованием алгоритма с полиномиальной сложностью по времени, как показано в алгоритме 14.3. Быстрый алгоритм возведения в степень был рассмотрен в лекциях 12-13. Размер исходного текста должен быть меньше чем n ; если размер исходного текста больше, то он должен быть разделен на блоки.
RSA_Encryption (P, e, n) // P — исходный текст в Zn и P < n
{
C <- Fast_Exponentiation (P, e, n) //Вычисление (Pe mod n)
return C
}
14.3.
Шифрование RSA
Дешифрование
Чтобы расшифровать сообщение зашифрованного текста, которое Боб получил в RSA, он может использовать алгоритм 14.4. Это можно выполнить, используя алгоритм с полиномиальной сложностью по времени, если размер зашифрованного текста меньше, чем n.
RSA_Decryption (C, d, n) //C — зашифрованный текст в Zn
{
P <- Fast_Exponentiation (C, d, n) // Вычисление (Cd mod n)
return P
}
14.4.
Дешифрование RSA
Доказательство RSА
Используя вторую версию теоремы Эйлера, которая обсуждалась в лекциях 12-13, мы можем доказать, что шифрование и дешифрование инверсны друг другу.

Предположим, что исходный текст, восстановленный Бобом, есть P1. Докажем, что он эквивалентен P.