| ВКР |
Поведение фирмы на финансовых рынках
Распределение финансовых средств фирмы
Теперь мы переходим к исследованию того, каким образом фирма решает, куда вкладывать денежные средства. Есть два основных направления их расходования: вложения в ценные бумаги и вложения в реальное производство. Первому способу посвящается анализ портфельного подхода фирмы к распределению средств по рискованным активам. Второй способ связан с анализом инвестиционных проектов.
Анализ оптимального портфеля ценных бумаг фирмы
Вложения в ценные бумаги других компаний называются рисковыми активами, так как поступления по ним отличаются большей или меньшей степенью нестабильности и неопределенности. Для снижения вероятности неудачи в случае рискованных активов распределение денежных средств происходит в виде портфеля - набора рискованных активов разного рода, оптимизация которого составляет главную задачу фирмы на финансовом рынке. Рассмотрим подробнее, каким образом осуществляется выбор фирмой оптимального портфеля рискованных активов - ценных бумаг.
К основным характеристикам портфель рискованных активов относятся такие их качества, как:
-
Доходность
Доходность определяется как средняя ожидаемая величина дохода набора ценных бумаг
где M - доходность портфель рискованных активов ; pi - вероятность получения дохода по i-му активу; yi - величина дохода от i-го актива.![M = \sum {\left[ {p_i *y_i } \right]} ,](/sites/default/files/tex_cache/a2b0a62dd7442731c2ba533902e807cd.png)
-
Рискованность
Рискованность портфеля вложений может быть оценена с помощью разного рода показателей.
- o дисперсия:
![s^2 = \sum {\left[ {p_i (y_i - M)^2 } \right]} = D](/sites/default/files/tex_cache/e08d18ac4ac88a326d7f1483a3ba10cf.png)
- o cтандартное отклонение:
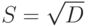
- o коэффициент вариации:
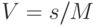
- o среднее квадратичное отклонение в доходах (SD) в динамике:где y - чистый доход за период t; ya - средний доход за период; n - количество лет наблюдений.
![SD = \sqrt {\left[ {S(y - y_a )^2 /n} \right]} ,](/sites/default/files/tex_cache/2363120f4a56aa2a3cb711101596f459.png)
- индекс нестабильности доходов при изменениях стоимости денежной единицы во времени:где yr - изменение доходов за период t, подсчитанное как
![I = \sqrt {\left[ {S(y - y^r )^2 /n} \right]} ,](/sites/default/files/tex_cache/2355f29170a21ee7e2f113d57b7f3a0e.png) где a - помехи, вызванные изменением стоимости денежной единицы (например, курса доллара как базы отсчета в случае с рублем); b - размер изменения; t - временной период.
где a - помехи, вызванные изменением стоимости денежной единицы (например, курса доллара как базы отсчета в случае с рублем); b - размер изменения; t - временной период.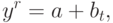
- o дисперсия:
Значения данных коэффициентов показывают относительный риск в зависимости от масштаба вложений. Высокие значения показателей указывают на низкое качество доходов, означают повышенный риск и отражают вариацию между действительными доходами и изменениями доходов.
Кривая безразличия фирмы при выборе портфеля вложений зависит от двух параметров - доходности активов и их рискованности: U = U(M, s), где M представляет собой доходность портфеля, а s является совокупной характеристикой его рискованности. Причем доходность является благом для фирмы, а рискованность - антиблагом, то есть  .
.
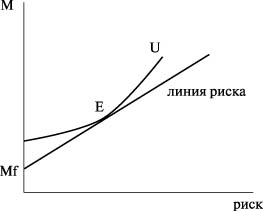
Если Mf - доход на безрисковый актив (например, государственные краткосрочные обязательства, получение дохода по которым практически всегда гарантировано правительством для любого периода времени и для любого экономического агента), то плата за дополнительный риск может быть выражена в виде дополнительного дохода для рисковых активов:
![\left[ {M - M_f } \right] = P*s,](/sites/default/files/tex_cache/49028ce142851143b1f2607f9dfe29c4.png)
Эта линия является линией бюджетного ограничения для фирмы, выбирающей портфель активов. Тогда равновесие на рынке рискованных активов будет в точке касания кривой безразличия и линии цены риска - линии бюджетного ограничения (рис. 7.4). Это будет точка оптимального соотношения доходности актива и его риска - точка Е.
Таким образом, оптимальный выбор фирмы представляет собой распределение денежных средств между рискованными активовами до тех пор, пока не будет выполняться следующее соотношение:
![- \left[ {\partial U/\partial s} \right]:\left[ {\partial U/\partial M} \right] = \left[ {M - M_f } \right]/s.](/sites/default/files/tex_cache/71f24d9d751908ea632bd5fd1cf0e16f.png)
Поскольку в портфель рискованных активов входят ценные бумаги разного рода, возможно возникновение взаимного влияния активов друг на друга. Измерение риска вложений при взаимном влиянии активов друг на друга происходит с помощью бета-коэффициента. Бета-коэффициент рассчитывается как
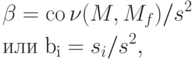
Бета-коэффициент характеризует систематический риск ценных бумаг, то есть он измеряет рискованность данного актива по сравнению с рискованностью рынка ценных бумаг в целом. Для безрискового актива  .
.
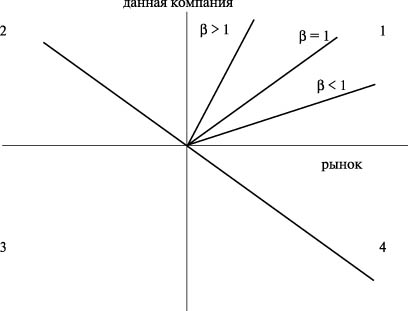
Бета-коэффициент показывает состояние экономической конъюнктуры в целом на рынке, он представляет собой тангенс угла наклона выявленной линейной зависимости между общерыночными прибылями по всем акциям на бирже в целом и прибылями по отдельным акциям. При сходном изменении рыночных цен и цен на конкретные ценные бумаги 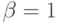 , то есть изменение общерыночной цена на 10% влечет за собой изменение на 10% цены данных бумаг. Если
, то есть изменение общерыночной цена на 10% влечет за собой изменение на 10% цены данных бумаг. Если 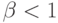 , то это означает слабую зависимость данных ценных бумаг от рынка в целом. Если
, то это означает слабую зависимость данных ценных бумаг от рынка в целом. Если 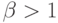 , это означает сильную зависимость. Эти зависимости отражены в квадранте 1 (рис. 7.5).
, это означает сильную зависимость. Эти зависимости отражены в квадранте 1 (рис. 7.5).
Если зависимость движения рынка и курса данных ценных бумаг противоположная, то она отражается в квадранте 3. Если на рынке происходит увеличение средних курсов при одновременном уменьшении курса данных акций, то это отразится в квадранте 2. При возникновении на рынке ситуации, когда средние курсы падают, а конкретный курс начинает расти, этот процесс отражается в квадранте 4. Это может характеризовать переломный момент в развитии фондового рынка.
Равновесие на рынке рискованных активов можно рассчитать с помощью коэффициента бета следующим образом. Цена единицы риска равна 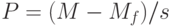 . Совокупный риск для i-го актива равен произведению единицы риска для этого актива и объему риска:
. Совокупный риск для i-го актива равен произведению единицы риска для этого актива и объему риска: 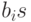 . Тогда цена совокупного риска равна
. Тогда цена совокупного риска равна 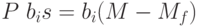 .
.
На рынке происходит выравнивание риска для всех активов, то есть
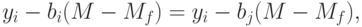
Такое выравнивание происходит и для безрискового актива. Поэтому
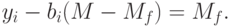
 - премия за риск.
- премия за риск.Модель оптимизации вложений с учетом отношения к риску
До сих пор мы рассматривали простую модель поведения фирмы при распределении портфеля рискованных активов, то есть мы учитывали только одну форму отношения фирмы к риску - отрицательное отношение к риску, несклонность менеджера, принимающего решение, рисковать вложенными средствами. Такая модель позволила проанализировать общие основы выбора фирмы. Теперь можно перейти к более сложному варианту функционирования фирмы, включив в модель типы поведения принимающего решения управляющего состава фирмы по отношению к риску.
Можно выделить три типа поведения менеджеров по отношению к риску, что определяет характер риска с точки зрения фирмы.
- Менеджеры не склонны к риску: в данном случае мы имеем обычный вид кривых безразличия, где риск - антиблаго, а доход - благо для фирмы; соответственно, мы получаем обычное состояние равновесия фирмы.
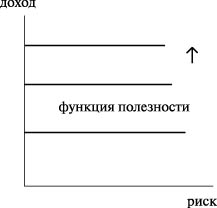
- Менеджеры нейтральны к риску: кривые безразличия представляют собой горизонтальные линии. Риск рассматривается как нейтральный товар, предпочитаемым благом по-прежнему является доходность портфеля (рис. 7.6).
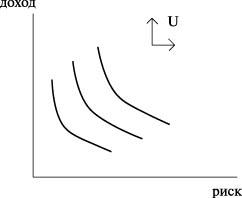
- Менеджеры, предпочитающие риск: здесь риск рассматривается как благо наряду с другим благом - доходностью. Поэтому кривые безразличия имеют обычный вид для двух благ (рис. 7.7).
В качестве бюджетного ограничения здесь принимается линия "риск-доход", которая имеет перевернутую U-образную форму: по мере роста риска доходность активов вначале увеличивается, достигая максимума, а затем сокращается - дополнительный риск перевешивает дополнительный доход. Соответственно, оптимальные соотношения риска и дохода будут зависеть от типа склонности к риску менеджера, принимающего решения, причем максимальное значение дохода достигается в случае нейтрального отношения менеджера к риску. Несклонность и предпочтение риска могут давать одинаковую доходность, но разную степень рискованности вложений.