Деление

Сложение и вычитание

Обе операции выполняются по сходным алгоритмам.

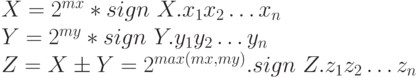
Операция выполняется следующим образом:

1. Находится разность порядков:
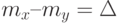
2. Производится выравнивание порядков, при этом если разность порядков положительна, то в качестве порядка результата берётся m_x, а мантисса M_y сдвигается вправо на |m_x– m_y| разрядов; еcли разрядность порядков отрицательна, то денормализуется мантисса M_x.
3. Производится алгебраическое суммирование мантисс слагаемых.
4. Выполняется нормализация влево или вправо на соответствующее число разрядов с необходимым исправлением порядка.

Пример:

порядок       мантисса
[mx]пк = 0.11 [Mx]пк = 0.1010
[my]пк = 0.10 [My]пк = 0.1110
Находим разность порядков:
    +00.11 = [mx]мок
     11.01 = [-my]мок
  1| 00.00
   |_ _->1

00.01 = - разность порядков.

Так как m x > my, то:
        +00.1010 = [Mx]мок
         00.0111 = [My]мок * 2-1
[Z]мок = 01.0001 – переполнение
         2-1 * [Z]мок = 00.1000 – нормализация
                max(mx,my) = [mx]мок = +00.11
                              [1]мок = 00.01
                             [mx]мок = 01.00 – переполнение порядка

Z = .

При выполнении операции сложения возможны следующие специфические случаи, называемые блокировками:

а) При определении разности порядков может оказаться, что необходимо мантиссу одного из чисел сдвигать на величину, большую, чем число разрядов в разрядной сетке. В этом случае, естественно, такое число может быть воспринято как нуль, а операция дальнейшего сложения может блокироваться, то есть не выполняться.

В качестве результата берётся максимальное число.

Пример:

[mx]ок = 0.101 [Mx]ок = 0.10111101
[my]ок = 1.001 [My]ок = 0.10000001

Разность порядков:

+00.101 = [mx]мок
 00.110 = [-my]мок

– то есть это число 11 ₁₀ , а в разрядной сетке мантиссы только 8 разрядов.

Поэтому операция блокируется, а результатом является число:

[mx] = 0.101 [Mx] = 0.10111101

Аналогичный случай может быть, когда разность порядков – отрицательна (отрицательное переполнение). В этом случае операция также блокируется, а результатом будет число с максимальным порядком.

Пример:

[mx]ок = 1.010 [Mx]ок = 1.10101011
[my]ок = 0.110 [My]ок = 1.11111111

Разность порядков:

+  11.010 = [mx]мок
   11.001 = [-my]мок
   _______
+1| 10.011
         1
   _______

10.100 =

То есть разность порядков меньше (-8).

Операция блокируется, а результатом будет число:

[my]ок = 0.110 [My]ок = 1.11111111

Десятичные двоично-кодированные системы.

Иногда в ЭВМ используются десятичные системы счисления. Их выгодно использовать тогда, когда объем исходных данных для обработки на ЭВМ – велик, сама обработка производится по относительно несложным программам. На этом происходит значительная экономия времени, которая вытекает из того, что не нужно делать перевод из десятичной в двоичную систему и обратно.

Как правило, в состав оборудования таких ЭВМ вводится АУ, работающее с числами в десятичной системе счисления. Поскольку в качестве основного запоминающего элемента используется триггер-ячейка с двумя устойчивыми состояниями, то каждая десятичная цифра кодируется совокупностью двоичных символов.

Перевод чисел из десятичной системы в десятичную двоично-кодированную выполняется исключительно просто, поразрядно и одновременно по всей сетке:

879,65_10 -> 1000 0111 1001, 0110 010110^-2

Аналогично, выполняется и обратный перевод:

0110 1001, 0101 001110^-2 -> 69, 5310

Существует большое разнообразие десятичных двоично-кодированных систем. Это многообразие вытекает из избыточности двоичного кода, при котором из 16 возможных комбинаций в каждом разряде используется по прямому информационному назначению лишь 10.

Наиболее широкое применение находят системы кодирования 8421 и 8421⁺³ (код Штибитца).

Система 8421 – неудобна тем, что при выполнении операции вычитания нет прямого перехода от цифры каждого разряда к дополнительному коду.

0000 - 0

0001 - 1

0010 - 2

0011 - 3

0100 - 4

0101 - 5

0110 - 6

0111 - 7

1000 - 8

1001 - 9

В то же время эта система обладает свойством аддитивности , поскольку результаты операции сложения над числами в десятичной системе и над их изображением в системе 8421 – совпадают.

Система 8421⁺³ - более интересна, т.к. она обладает свойством самодополнения. Видно, что дополнение до 9 можно получить, применяя операцию поразрядного инвертирования кода.

0011 – 0

0100 – 1

0101 – 2

0110 – 3

0111 – 4

1000 – 5

1001 – 6

1010 – 7

1011 – 8

1100 – 9

Всего существует А₁₆¹⁰ = 2,9•10¹⁰ вариантов 10-ых двоично-кодированных систем.