Совершенные дизъюнктивные и конъюнктивные нормальные формы ФАЛ
Введем понятие степени:
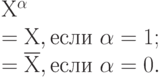
Рассмотрим конъюнкцию вида:

Существует 2n наборов вида 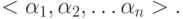 Поставим в соответствие каждой конъюнкции (*) номер набора i и образуем дизъюнкцию всех конъюнкций:
Поставим в соответствие каждой конъюнкции (*) номер набора i и образуем дизъюнкцию всех конъюнкций:
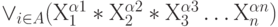
Теорема (без доказательства):
Любая ФАЛ, зависящая от ' n ' аргументов, может быть представлена в форме:
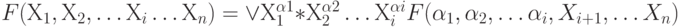
Из этой теоремы вытекает ряд важных следствий:
- Она дает возможность перейти от табличного задания функции к аналитической форме и сделать обратный переход.
- Устанавливает так называемую функциональную полноту связок (базиса) "
 -", т.к. позволит построить в этом базисе произвольную ФАЛ от произвольного числа аргументов.
-", т.к. позволит построить в этом базисе произвольную ФАЛ от произвольного числа аргументов.
Примечание:
- Если
 то соответствующая форма функции называется дизъюнктивной нормальной (ДНФ).
то соответствующая форма функции называется дизъюнктивной нормальной (ДНФ). - Если i=n, то каноническая форма функции носит название совершенной ДНФ (СДНФ). Дизъюнкции берутся по тем наборам, на которых функция f(X_{1},X_{2},...,X_{n})=1
Пример: ДНФ
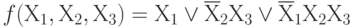

В ДНФ в каждый член любая переменная входит в прямом виде или с отрицанием.
Аналогичная теорема справедлива и для представления функции в конъюнктивной нормальной форме (КНФ):
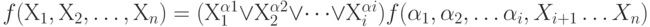
или при представлении в совершенной КНФ (СКНФ):
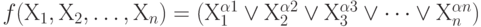
где: & означает, что конъюнкции берутся по тем наборам, на которых
f(Х_{1}, Х_{2}, ... Х_{n})=0.Дадим на основании этих теорем правило перехода от табличной формы функции к СДНФ и СКНФ.
Переход от табличной формы функции к СДНФ или правило записи функции по единицам:
- Выбрать те наборы аргументов, на которых f(Х_{1}, Х_{2}, ... Х_{n})=1.
- Выписать все конъюнкции для этих наборов. Если при этом Х_{i} имеет значение ' 1 ', то этот множитель пишется в прямом виде, если ' 0 ', то с отрицанием.
- Все конъюнктивные члены соединить знаком дизъюнкции
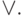
Пример:
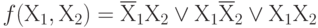
Правило перехода от табличной формы задания функции к СКНФ или правило записи функции по нулям.
- Выбрать те наборы аргументов, на которых f(Х_{1}, Х_{2}, ... Х_{n})=0.
- Если при этом Х_{i} имеет значение ' 0 ', то остается без изменений. Если ' 1 ', то с отрицанием.
- Все дизъюнктивные члены соединить знаком конъюнкции
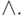
Пример:

Пример:
| X_{1} | Х_{2} | Х_{3} | f(Х_{1}, Х_{2}, Х_{3}) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
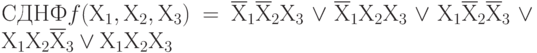
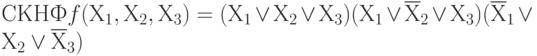
Рассмотрим способ получения СДНФ из СКНФ и обратно.
Из таблицы 2.1 с помощью способа записи функции по нулям следует, что СКНФ той же функции дизъюнкции будет иметь вид:

Итак, имеем две формы одной и той же функции:
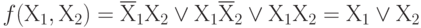
Итак, видно, что общее число членов в этих двух формах равно сумме нулей и единиц функции, то есть равно 2n.
Если в исходной форме функции, записанной в СКНФ или СДНФ, содержится z членов, то в другой ее форме (т.е. СДНФ или СКНФ ) их будет (2n- z).
Поскольку в функцию мы включаем дизъюнктивные или конъюнктивные члены и берем их по наборам, на которых функция или обращается в ' 0 ', или в ' 1 ', то для перехода от одной формы задания функции к другой нужно выписать все недостающие члены и поставить над каждой переменной отрицание, а также заменить знаки конъюнкции на дизъюнкцию и обратно.

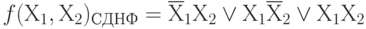
Практический смысл перехода заключается в том, что можно определить, реализация какой формы потребует меньший объем оборудования.

