Арифметические основы

Перевод чисел из одной системы счисления в другую.

Всякий раз, когда используется для вычислений система счисления, отличная от фактической, необходимо выполнить перевод 10 => p, p => 10.

Есть системы, дающие значительно более высокие скорости, но и требующие большего количества оборудования.

Этот перевод может быть выполнен:

1. вручную,
2. на ЭВМ (с помощью специальных программ).

Во всех этих случаях принципиально используется различные подход и методы. В связи с тем, что нам придется готовить информацию для программы вручную, мы рассмотрим, прежде всего, методы, направленные на ручной перевод.

Итак, имеем дело с позиционной системой счисления с основанием " p ", с естественными весами разрядов.

В качестве промежуточной используется, естественно, десятичная система. Вначале число переводится из системы " p " в 10-ую, затем из 10-ой в систему с нужным основанием.

Мы отступим от этого правила и воспользуемся алгоритмом непосредственного перевода из системы с основанием " p " в систему с основанием " q ".

Обычно произвольное число, содержащее целую и дробную части, переводят по частям: вначале целую, затем дробную часть.

Рассмотрим перевод целых чисел:

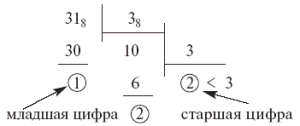
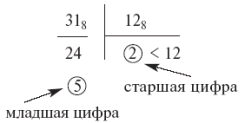
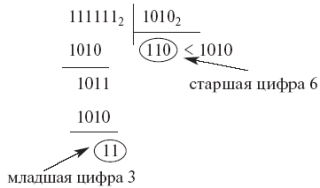
Перевод осуществляется по следующему правилу: исходное число, записанное в системе с основанием " p " и его частные последовательно делятся на число " q ", представленное в системе " p ". Деление производится в системе с основанием " p " и продолжается до получения результата, меньшего " q ". Первый остаток, меньший " q ", дает старшую цифру числа N_q. Остатки от деления дают остальные цифры числа N_q.

Пример:

1. 3110 => 2;   3110 = 111112

   

   
   

2. 318 => 3;  318 = 2213 = 
   2*32 + 2*31 + 1*30 = 18 + 6 + 1 = 2510.

   

   
   

3. 318 => 10;  318 = 2510.

   

   
   

4. 1111112 => 10;  1111112 = 6310.

   

   
   

Перевод дробных чисел из системы с основанием " p " в систему с основанием " q " выполняется по следующему правилу: исходное число D_p последовательно умножается на число " q ", записанное в системе " p ". Целые части получаемых произведений дают " p "-ые записи " q "-х цифр, начиная со старшей. Умножение производится в системе с основанием " p " до получения необходимой точности.

Пример:

1. 0,5314₈ => 5; 0,5314₈ = 0,3141...₅.

   0,	53148 58
   3	2774 5
   1	6754 5
   4	2634 5
   1	6014
2. 0,318₁₀ => 2; 0,318₁₀ = 0,01010...₂.

   0,	31810 210
   0	636 2
   1	272 2
   0	544 2
   1	088 2
   0	176
3. 0,5314₈ => 10; 0,5314₈ = 0,674...₁₀

   0,	53148 128
   1 5	2630 314
   6	57708 128
   1 5	3760 770
   7	36608 128
   1 3	7540 660
   4	6340