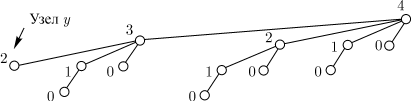
|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Тонкие кучи
Операция DeleteMin(H).
Эта операция предназначена для удаления узла с минимальным
ключом из непустой кучи  . Для ее реализации удаляем минимальный
узел из корневого списка кучи
. Для ее реализации удаляем минимальный
узел из корневого списка кучи  , добавляем список детей удаленного
узла в корневой список и повторяем следующий "связывающий шаг".
, добавляем список детей удаленного
узла в корневой список и повторяем следующий "связывающий шаг".
Находим любые два дерева, корни которых имеют одинаковые ранги,
и связываем их, делая корень с большим ключом новым левым потомком корня
с меньшим ключом, увеличивая ранг нового полученного тонкого дерева на
единицу. При этом следует удалить из корневого списка кучи  корень с большим ключом. Как только не останется деревьев с корнями одинакового
ранга, в полученном корневом списке необходимо найти элемент с минимальным
ключом.
корень с большим ключом. Как только не останется деревьев с корнями одинакового
ранга, в полученном корневом списке необходимо найти элемент с минимальным
ключом.
Рассмотрим теперь, с помощью каких средств реализуется связывающий шаг.
Для хранения ссылок на корни деревьев используем временный
массив  , размера
, размера  . Величина
. Величина ![{\rm RankT}[i]](/sites/default/files/tex_cache/8291d6c8c038f0ccbdd9a6b6796ee98d.png) будет
указателем на тонкое дерево ранга
будет
указателем на тонкое дерево ранга  . Если найдется еще одно дерево
ранга
. Если найдется еще одно дерево
ранга  , то свяжем два дерева ранга
, то свяжем два дерева ранга  в одно дерево
ранга
в одно дерево
ранга  , в
, в  -й ячейке массива
-й ячейке массива  установим нулевой
указатель и продолжим связывающую процедуру с вновь полученным деревом
ранга
установим нулевой
указатель и продолжим связывающую процедуру с вновь полученным деревом
ранга  .
.
При включении списка детей необходимо учесть возможность помеченности
детей минимального узла. То есть уменьшить их ранг там, где это
необходимо. Это требование вытекает из свойства 2 определения тонкого
дерева. Очевидно, что для проверки помеченности узла требуется  операций.
операций.
В результате выполнения связывающих шагов получаем заполненный
массив  . Теперь остается только связать все деревья,
находящиеся в этом массиве, в корневой список и найти в этом списке новый минимальный
элемент. Очевидно, все это можно выполнить
с трудоемкостью
. Теперь остается только связать все деревья,
находящиеся в этом массиве, в корневой список и найти в этом списке новый минимальный
элемент. Очевидно, все это можно выполнить
с трудоемкостью  .
.
Чтобы оценить амортизационную стоимость операции  ,
подсчитаем фактическую стоимость операции и изменение потенциала.
Фактическая стоимость складывается из
,
подсчитаем фактическую стоимость операции и изменение потенциала.
Фактическая стоимость складывается из  операций на проверку
кучи на пустоту,
операций на проверку
кучи на пустоту,  действий при добавлении детей
минимального узла в корневой список и
действий при добавлении детей
минимального узла в корневой список и  (количество связывающих
шагов) +
(количество связывающих
шагов) +  при выполнении связывающих шагов.
при выполнении связывающих шагов.
В итоге фактическая стоимость операции удаления минимального элемента есть  (количество связывающих шагов) +
(количество связывающих шагов) +  .
.
Очевидно, что потенциал уменьшился, как минимум, на число связывающих
шагов, так как при каждом связывающем шаге количество деревьев в корневом
списке уменьшается на единицу. Поскольку амортизационная стоимость равна
фактической стоимости плюс изменение потенциала, то амортизационная
стоимость равна  .
.
Операция DecreaseKey 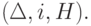 При уменьшении ключа у некорневого элемента
При уменьшении ключа у некорневого элемента  в куче
в куче  на величину
на величину  может быть нарушено свойство
кучеобразности. Для восстановления этого свойства
перемещаем поддерево с корнем в изменяемом
элементе в корневой список, но при этом, возможно, оставшееся после
переноса дерево может не оказаться тонким.
может быть нарушено свойство
кучеобразности. Для восстановления этого свойства
перемещаем поддерево с корнем в изменяемом
элементе в корневой список, но при этом, возможно, оставшееся после
переноса дерево может не оказаться тонким.
Покажем, как, затратив  амортизированного времени,
исправлять его структуру. В процедуре
амортизированного времени,
исправлять его структуру. В процедуре 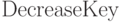 после уменьшения
ключа корректируется, если это необходимо, указатель на минимальный
элемент кучи. После этого проверяется, не является ли измененный
узел
после уменьшения
ключа корректируется, если это необходимо, указатель на минимальный
элемент кучи. После этого проверяется, не является ли измененный
узел  корнем дерева
корнем дерева  . Если это действительно так, то процедура
завершается, в противном случае переносим поддерево с корнем
в узле
. Если это действительно так, то процедура
завершается, в противном случае переносим поддерево с корнем
в узле  в корневой список кучи и запускаем процедуру коррекции
оставшегося дерева
в корневой список кучи и запускаем процедуру коррекции
оставшегося дерева 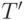 .
.
Будем различать два вида нарушений свойств тонкого дерева:
- Братские нарушения — это нарушения третьего правила из определения тонкого дерева.
- Родительские нарушения — это нарушения первого или второго правила.
Рассмотрим подробнее каждое из двух видов нарушений. Назовем
узел  узлом локализации братского нарушения среди детей узла
узлом локализации братского нарушения среди детей узла  , если
ранг узла
, если
ранг узла  отличается от ранга его ближайшего правого брата на 2,
либо он не имеет правого брата и его ранг равен 1. Пример —
на рис. 8.3.
отличается от ранга его ближайшего правого брата на 2,
либо он не имеет правого брата и его ранг равен 1. Пример —
на рис. 8.3.
Назовем узел  узлом локализации родительского нарушения,
если выполнено одно из трех условий:
узлом локализации родительского нарушения,
если выполнено одно из трех условий:
-
Ранг узла
 на три больше, чем ранг его
самого левого сына.
на три больше, чем ранг его
самого левого сына. -
Ранг узла
 равен двум, и он не имеет детей.
равен двум, и он не имеет детей. - Узел
 есть помеченный корень дерева.
есть помеченный корень дерева.
Пример приведен на рис. 8.4.