|
на стр 6, лекции 3, Очевидно "Ck <= модуль(Gk(е))*b(k+1)" (1) - , подскажите что значит "модуль" и почему это очевидно... |
Толстые кучи
Рассматриваемое в этой лекции представление приоритетной очереди основано на использовании так называемых избыточных счетчиков, позволяющих за время O(1) инкрементировать любой разряд. Заметим, что использованные здесь счетчики — лишь один из способов реализации толстых куч. На самом деле, для их реализации подойдет произвольный d-арный счетчик, при условии, что трудоемкость инкрементирования любого его разряда является константной.
Избыточное представление чисел
Основные определения.
Избыточным  -арным
представлением неотрицательного целого числа
-арным
представлением неотрицательного целого числа  будем считать
последовательность
будем считать
последовательность 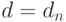 ,
, 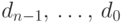 , такую, что
, такую, что
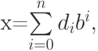
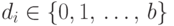 ,
,  .
Будем называть
.
Будем называть  цифрой, стоящей в
цифрой, стоящей в  -м
разряде. В примерах запятые между цифрами опускаем.
-м
разряде. В примерах запятые между цифрами опускаем.Заметим, что избыточное представление отличается от обычного  -арного представления использованием "лишней"
цифры
-арного представления использованием "лишней"
цифры  , что
приводит к неоднозначности представления чисел. Например, при
, что
приводит к неоднозначности представления чисел. Например, при 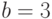 число
число  может быть представлено как
может быть представлено как  и
как
и
как  .
.
В примерах, в которых 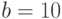 , "цифру" 10 будем
обозначать
символом
, "цифру" 10 будем
обозначать
символом  .
.
Назовем  -арное избыточное представление числа регулярным, если в нем между любыми двумя цифрами,
равными
-арное избыточное представление числа регулярным, если в нем между любыми двумя цифрами,
равными  , найдется цифра, отличная от
, найдется цифра, отличная от  .
.
Пример.
Пусть 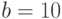 , а число
, а число  представляется
в обычной десятичной системе последовательностью
представляется
в обычной десятичной системе последовательностью 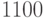 , тогда
представления
, тогда
представления  и
и 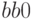 не являются регулярными
не являются регулярными  -арными избыточными представлениями числа
-арными избыточными представлениями числа  ,
а представления
,
а представления 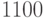 и
и  регулярны.
регулярны.
Пусть  — номер разряда, отличного от
— номер разряда, отличного от  и ближайшего слева от
и ближайшего слева от  -го разряда в регулярном
-го разряда в регулярном  -арном избыточном представлении
-арном избыточном представлении  .
.
Определим 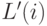 следующим образом:
следующим образом:  ,
если
,
если  ,
, 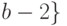 и
и 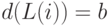 ;
; 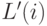 — произвольное число
— произвольное число 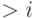 , если
, если  и
и  ;
; 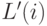 — не определено,
если
— не определено,
если 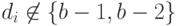 .
.
Величину 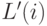 будем называть прямым указателем.
Пусть
будем называть прямым указателем.
Пусть 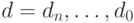 —
—  -арное
регулярное представление
некоторого числа.
-арное
регулярное представление
некоторого числа.
Фиксацией цифры b, стоящей в i-м разряде
представления d, 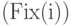 назовем операцию, заключающуюся в обнулении цифры
назовем операцию, заключающуюся в обнулении цифры  и инкрементировании цифры
и инкрементировании цифры 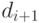 , при этом если
, при этом если 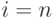 , то полагаем
, то полагаем 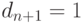 . При каждом выполнении
операции фиксации будем обновлять значение
. При каждом выполнении
операции фиксации будем обновлять значение 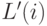 . Очевидно,
при
. Очевидно,
при 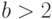 операцию
операцию 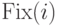 можно выполнить
с помощью следующих операторов.
можно выполнить
с помощью следующих операторов.
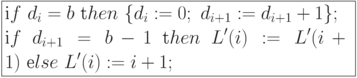
Инкрементирование i-й цифры избыточного
представления d  можно выполнить
с помощью операторов
можно выполнить
с помощью операторов
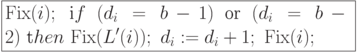
Очевидно, что инкрементирование  -го разряда регулярного
-го разряда регулярного  -арного избыточного представления числа
-арного избыточного представления числа  производит представление числа
производит представление числа 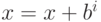 .
.
Нетрудно доказать, что операции фиксации и инкрементирования, примененные
к регулярному избыточному представлению, не нарушают регулярности и
корректно вычисляют указатели  с
трудоемкостью
с
трудоемкостью  .
.
Эта схема может быть расширена для выполнения за константное время
декрементирования произвольной цифры добавлением дополнительного цифрового
значения 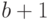 . Оставляем детали в качестве упражнения.
. Оставляем детали в качестве упражнения.
Толстые деревья
Основные определения
Определяем толстое
дерево  ранга
ранга 
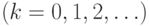 следующим образом:
следующим образом:
-
Толстое дерево
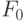 ранга ноль состоит из
единственного узла.
ранга ноль состоит из
единственного узла. -
Толстое дерево
 ранга
ранга  ,
для
,
для  , состоит из трех деревьев
, состоит из трех деревьев 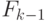 ранга
ранга  , связанных так, что корни двух из них являются самыми
левыми потомками корня третьего.
, связанных так, что корни двух из них являются самыми
левыми потомками корня третьего.
Ранг узла  в толстом
дереве определяется как ранг толстого поддерева с корнем в узле
в толстом
дереве определяется как ранг толстого поддерева с корнем в узле  .
.
На рис. 9.1 приведены примеры толстых деревьев.
Свойства толстых деревьев:
- В толстом дереве ранга
 ровно
ровно 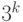 узлов.
узлов. - Для любого натурального числа
 существует лес из толстых
деревьев, в котором ровно
существует лес из толстых
деревьев, в котором ровно  узлов. Такой лес можно построить,
включив в него столько деревьев ранга
узлов. Такой лес можно построить,
включив в него столько деревьев ранга  , каково
значение
, каково
значение  -го разряда представления числа
-го разряда представления числа  в троичной системе счисления.
Заметим, что для построения такого леса можно использовать и избыточные троичные
представления.
в троичной системе счисления.
Заметим, что для построения такого леса можно использовать и избыточные троичные
представления. - Толстый лес из
 узлов содержит
узлов содержит  деревьев.
деревьев.
Доказательства этих свойств оставим читателю в качестве упражнения.
Рассмотрим лес из нескольких толстых деревьев, ранги которых не
обязательно попарно различны и узлам которых взаимно однозначно поставлены
в соответствие элементы взвешенного множества. Такой лес будем называть
нагруженным. Узел в нагруженном лесе назовем неправильным, если его ключ
меньше ключа его родителя. Нагруженный лес назовем почти кучеобразным,
если для каждого значения  в нем имеется не более двух
неправильных узлов ранга
в нем имеется не более двух
неправильных узлов ранга  .
.

