НОУ ИНТУИТ | Управление инвестиционным проектом. Лекция 13: Принятие оптимального инвестиционного решения в условиях риска и неопределенности

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 08.02.2012 | Уровень: для всех | Доступ: свободно

Чтобы определить критерий Вальда, нужно выбрать в матрице доходности проект, который даст наибольшую доходность при реализации пессимистического сценария:

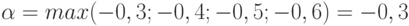
$\alpha=max(-0,3; -0,4; -0,5; -0,6)= - 0,3$

Оптимальным по критерию Вальда является проект А.

Для определения критерия Сэвиджа нужно выбрать в матрице рисков проект, для которого в случае реализации пессимистического сценария риск будет минимальным:

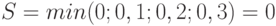
Оптимальным по критерию Сэвиджа является проект А.

Рассчитаем критерий Гурвица:

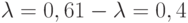
$\lambda=0,6\\1-\lambda=0,4$

В каждой строке матрицы доходности минимальная доходность соответствует пессимистическому сценарию, а максимальная – оптимистическому.

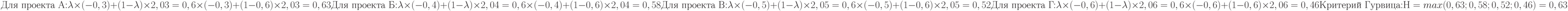
$\text{Для проекта А:}\\ \lambda\times (-0,3)+(1-\lambda)\times 2,03= 0,6\times (-0,3)+(1-0,6) \times 2,03=0,63\\ \text{Для проекта Б:}\\ \lambda\times (-0,4)+(1-\lambda) \times 2,04= 0,6\times (-0,4)+(1-0,6) \times 2,04=0,58\\ \text{Для проекта В:}\\ \lambda\times (-0,5)+(1-\lambda)\times 2,05= 0,6\times (-0,5)+(1-0,6) \times 2,05=0,52\\ \text{Для проекта Г:}\\ \lambda\times (-0,6)+(1-\lambda)\times 2,06= 0,6\times (-0,6)+(1-0,6) \times 2,06=0,46\\ \text{Критерий Гурвица:}\\ Н=max(0,63; 0,58; 0,52; 0,46)=0,63\\$

Оптимальным по критерию Гурвица является проект А.

Чтобы рассчитать критерий Байеса, нужно составить новую матрицу, умножив каждый элемент матрицы доходности на вероятность наступления соответствующего сценария ( таблица 13.5 таблица 13.6):

Таблица 13.5. Составление матрицы для расчета критерия Байеса
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
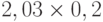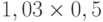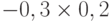Проект А	$2,03 \times 0,2$	$1,03 \times 0,5$	$-0,3 \times 0,2$	$1,01 \times 0,1$
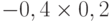Проект Б	$2,04 \times 0,2$	$1,04 \times 0,5$	$-0,4 \times 0,2$	$1,02 \times 0,1$
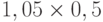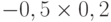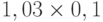Проект В	$2,05 \times 0,2$	$1,05 \times 0,5$	$-0,5 \times 0,2$	$1,03 \times 0,1$
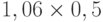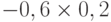Проект Г	$2,06 \times 0,2$	$1,06 \times 0,5$	$-0,6 \times 0,2$	$1,04 \times 0,1$

Рассчитав значения элементов, получим:

Таблица 13.6. Матрица для расчета критерия Байеса
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
Проект А	0,41	0,52	-0,06	0,10
Проект Б	0,41	0,52	-0,08	0,10
Проект В	0,41	0,53	-0,10	0,12
Проект Г	0,41	0,53	-0,12	0,13

Определяем сумму по строкам матрицы.

Проект А:

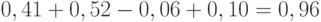
Проект Б:

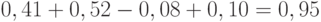
Проект В:

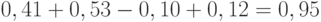
Проект Г:

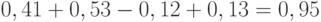
Критерий Байеса:

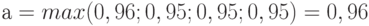
Оптимальным по критерию Байеса является проект А.

Для расчета критерия Лапласа также нужно составить дополнительную матрицу. Принцип ее составления остается таким же, как при расчете критерия Байеса, но вероятности наступления сценария принимаются равными, то есть по 0,25 ( таблица 13.7 таблица 13.8).

Таблица 13.7. Составление матрицы для расчета критерия Лапласа
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
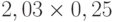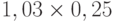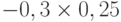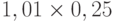Проект А	$2,03 \times 0,25$	$1,03 \times 0,25$	$-0,3 \times 0,25$	$1,01 \times 0,25$
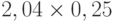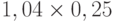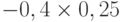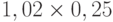Проект Б	$2,04 \times 0,25$	$1,04 \times 0,25$	$-0,4 \times 0,25$	$1,02 \times 0,25$
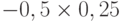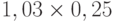Проект В	$2,05 \times 0,25$	$1,05 \times 0,25$	$-0,5 \times 0,25$	$1,03 \times 0,25$
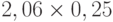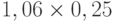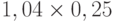Проект Г	$2,06 \times 0,25$	$1,06 \times 0,25$	$-0,6 \times 0,25$	$1,04 \times 0,25$

Рассчитав значения элементов, получим:

Таблица 13.8. Матрица для расчета критерия Лапласа
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
Проект А	0,51	0,26	-0,08	0,25
Проект Б	0,51	0,26	-0,10	0,26
Проект В	0,51	0,26	-0,13	0,29
Проект Г	0,52	0,27	-0,15	0,33

Далее определяем суммы по строкам матрицы.

$\text{Проект А: }0,51+0,26-0,08+0,25=0,94\\ \text{Проект Б: } 0,51+0,26-0,10+0,26=0,93\\ \text{Проект В: }0,51+0,26-0,13+0,29=0,94\\ \text{Проект Г: }0,52+0,27-0,15+0,33=0,96\\ \text{Критерий Лапласа: }l=max(0,94; 0,93; 0,94; 0,96)=0,96$

Оптимальным по критерию Лапласа является проект Г.

Краткие итоги:

Хозяйственная деятельность связана с постоянным выбором вариантов инвестирования.
Для выбора оптимального варианта инвестирования рассчитываются критерии Вальда, Сэвиджа, Гурвица, Байеса и Лапласа.
Для расчета критериев необходимо составление матрицы доходности и матрицы рисков.
Критерии Вальда и Сэвиджа олицетворяют позицию "крайнего пессимизма", но критерий Вальда ориентируется на доходность, а критерий Сэвиджа — на риск.
Для расчета критерия Гурвица используется коэффициент пессимизма.
Критерии Байеса и Лапласа указывают на тот проект, для которого математическое ожидание доходности максимально.

Упражнения:

Охарактеризуйте проблему принятия инвестиционного решения в условиях неопределенности.
Перечислите основные критерии выбора оптимального решения в условиях неопределенности.
Приведите формулы для расчета критериев Вальда, Сэвиджа, Гурвица, Байеса, Лапласа.

Дана матрица доходности. Составить матрицу рисков:

вариант 1
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
Проект А	2,9	2	1	2
Проект Б	3,8	3	2	2,3
Проект В	4,6	4	3	2,7
Проект Г	3,1	3,1	0,5	2,9

вариант 2
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
Проект А	1,9	1	1	1
Проект Б	1,8	1	1	1,1
Проект В	4,6	4	1	1,7
Проект Г	1,1	1,1	0,5	1,9

Рассчитать критерии Вальда, Сэвиджа, Гурвица, Байеса, Лапласа, используя матрицы доходности и рисков из предыдущего задания (упраженение 4).

Темы для курсовых работ, рефератов, эссе:

Проблема выбора оптимального варианта инвестирования в современной экономике.
Экономико-математические методы оценки риска инвестиционного проекта.

Дальше >>

Управление инвестиционным проектом

Принятие оптимального инвестиционного решения в условиях риска и неопределенности

Краткие итоги:

Упражнения:

Темы для курсовых работ, рефератов, эссе:

Вопросы и ответы

Студенты

Авторизоваться

Управление инвестиционным проектом

Принятие оптимального инвестиционного решения в условиях риска и неопределенности

Краткие итоги:

Упражнения:

Темы для курсовых работ, рефератов, эссе:

Вопросы и ответы

Студенты