|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Квадратичное сравнение
Мы ограничим наше обсуждение только квадратичными уравнениями, в которых a2 = 1 и a1 = 0. Тогда рассмотрение будет касаться уравнений следующей формы:
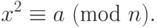
Квадратичное сравнение с модулем в виде простого числа
Мы сначала рассматриваем случай, в котором модуль является простым числом. Другими словами, мы хотим найти решения уравнения формы  , в котором p является простым числом и a — целое число, такое, что p и a — взаимно простые. Может быть доказано, что этот тип уравнения либо не имеет никакого решения, либо имеет только два неконгруэнтных решения.
, в котором p является простым числом и a — целое число, такое, что p и a — взаимно простые. Может быть доказано, что этот тип уравнения либо не имеет никакого решения, либо имеет только два неконгруэнтных решения.
Пример 13.1
Уравнение  имеет два решения:
имеет два решения: 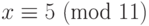 и
и 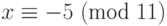 . Но заметим, что
. Но заметим, что  , так что фактически эти два решения 5 и 6. Также обратите внимание, что эти два решения неконгруэнтны (несравнимы).
, так что фактически эти два решения 5 и 6. Также обратите внимание, что эти два решения неконгруэнтны (несравнимы).
Пример 13.2
Уравнение  не имеет решения. Не может быть найдено ни одного целого числа x, такого, что квадрат равен 2 mod 11.
не имеет решения. Не может быть найдено ни одного целого числа x, такого, что квадрат равен 2 mod 11.
Квадратичные вычеты и невычет
В уравнении 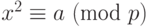 . a называется квадратичным вычетом (QR), если уравнение имеет два решения; a называется квадратичным невычетом (QNR), если уравнение не имеет решений. Может быть доказано, что в ZP* с p – 1 элементами (p – 1)/2 элементов — квадратичные вычеты и (p – 1)/2 являются квадратичными невычетами.
. a называется квадратичным вычетом (QR), если уравнение имеет два решения; a называется квадратичным невычетом (QNR), если уравнение не имеет решений. Может быть доказано, что в ZP* с p – 1 элементами (p – 1)/2 элементов — квадратичные вычеты и (p – 1)/2 являются квадратичными невычетами.
Пример 13.3
Есть 10 элементов в Z11*. Пять из них – квадратичные вычеты, и пять — невычеты. Другими словами, Z11* может быть разделен на два отдельных множества, QR и QNR, как это показано на рис. 13.1.
Критерий Эйлера
Как мы можем проверить, является ли целое число QR по модулю p? Критерий Эйлера дает признаки:
a. Если 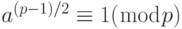 — квадратичный вычет по модулю p.
— квадратичный вычет по модулю p.
b. Если  — квадратичный невычет по модулю p.
— квадратичный невычет по модулю p.
Пример 13.4
Для того чтобы узнать, является ли 14 или 16 QR в Z11*, сделаем следующие вычисления:
14(23-1)/2 mod 23 1411 mod 23 -> 22 mod 23 -> –1 mod 23 невычет 16(23-1)/2 mod 23 1611 mod 23 -> 1 mod 23 вычет
Решение квадратичного сравнения с модулем в виде простого числа
Хотя критерий Эйлера позволяет нам определить, является ли целое число a QR или QNR в Zp*, он не может найти решение  . Чтобы найти решение этого квадратного уравнения, мы заметим, что простое число может быть представлено либо как p = 4k + 1, либо как p = 4 к + 3, в котором k является положительным целым числом. Решение квадратного уравнения — очень сложное в первом случае и более простое во втором. Мы обсудим только второй случай, который мы будем использовать в лекциях 14-15, когда будем рассматривать криптографическую систему Рабина.
. Чтобы найти решение этого квадратного уравнения, мы заметим, что простое число может быть представлено либо как p = 4k + 1, либо как p = 4 к + 3, в котором k является положительным целым числом. Решение квадратного уравнения — очень сложное в первом случае и более простое во втором. Мы обсудим только второй случай, который мы будем использовать в лекциях 14-15, когда будем рассматривать криптографическую систему Рабина.
Специальный случай: p = 4 К + 3, если p находится в форме 4 К + 3 (то есть p = 3 mod 4 ) и a есть QR в Zp*, то
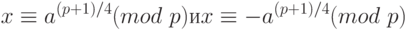
Пример 13.5
Решите следующие квадратные уравнения:
a. 
b. 
c. 
Решения
a. В первом уравнении 3 - QR в Z23, решение - 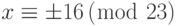 . Другими словами,
. Другими словами,  .
.
b.Во втором уравнении 2 - QNR в Z11. Нет решения для 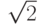 в Z11.
в Z11.
c. В третьем уравнении 7 - QR в Z19, решение -  . Другими словами
. Другими словами  .
.
Квадратичное сравнение по составному модулю
Квадратичное сравнение по составному модулю может быть приведено к решению системы сравнений по модулю в виде простого числа. Другими словами, мы можем анализировать 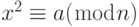 , если имеем разложение n на множители. Теперь мы можем решить каждое анализируемое уравнение (если оно разрешимо) и найти k пар ответов для x, как показано на рис. 13.2.
, если имеем разложение n на множители. Теперь мы можем решить каждое анализируемое уравнение (если оно разрешимо) и найти k пар ответов для x, как показано на рис. 13.2.
Из k пар ответов мы можем составить 2 системы уравнений, которые могут быть решены с использованием китайской теоремы об остатках, чтобы найти 2 значения для x. В криптографии обычно n выбирают так, чтобы 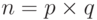 , — это означает k = 2, и мы имеем в целом только четыре ответа.
, — это означает k = 2, и мы имеем в целом только четыре ответа.
Пример 13.6
Предположим, что 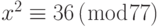 . Мы знаем, что
. Мы знаем, что 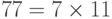 . Мы можем написать
. Мы можем написать

Обратите внимание, что мы выбрали 3 и 7, чтобы иметь форму 4k + 3 — так, чтобы мы могли решить уравнения, основываясь на предыдущих рассуждениях. Из этих уравнений мы имеем квадратичные вычеты в собственном множестве. Ответы 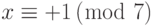 ,
, 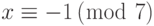 ,
, 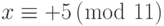 и
и  . Теперь мы можем из них составить четыре системы уравнений:
. Теперь мы можем из них составить четыре системы уравнений:
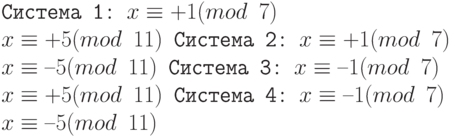
Ответы : 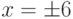 и
и 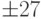 .
.
Сложность
Как сложно решить квадратичное сравнение по составному модулю? Главная задача — это разложение модуля на множители. Другими словами, сложность решения квадратичного сравнения по составному модулю — такая же, как и разложения на множители составного целого числа. Как мы видели раньше, если n очень большое, то разложение на множители неосуществимо.