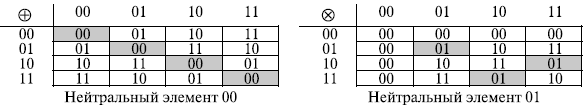|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Поля
Поля GF(2n)
В криптографии мы часто должны использовать четыре операции (сложение, вычитание, умножение и деление). Другими словами, мы должны использовать поля. Однако когда мы работаем с компьютерами, положительные целые числа сохраняются в компьютере как n -битовые слова, в которых n является обычно 8, 16, 32, 64, и так далее. Это означает, что диапазон целых чисел — 0 до 2n – 1. Модуль — 2n. Так что возможны два варианта, если мы хотим использовать поле.
1. Мы можем задействовать GF(p) с множеством Zp, где p — наибольшее простое число, меньшее, чем 2n. Но эта схема неэффективна, потому что мы не можем использовать целые числа от p до 2n- 1. Например, если n = 4, то наибольшее простое число, меньшее, чем 24, — это 13. Это означает, что мы не можем использовать целые числа 13, 14 и 15. Если n = 8, наибольшее простое число, меньшее, чем 28, — это 251, так что мы не можем использовать 251, 252, 253, 254 и 255.
2. Мы можем работать в GF(2n) и использовать множество 2n элементов. Элементы в этом множестве — n -битовые слова. Например, если n = 3, множество равно:
{000,001,010,011, 100,101,110,111}Однако мы не можем интерпретировать каждый элемент как целое число от 0 до 7, потому что не могут быть применены обычные четыре операции (модуль 2n — не простое число). Мы должны определить множество слов по 2 бита и две новых операции, которые удовлетворяют свойствам, определенным для поля.
Пример 6.1
Определим GF(22) поле, в котором множество имеет четыре слова по 2 бита: {00, 01, 10, 11}. Мы можем переопределить сложение и умножение для этого поля таким образом, чтобы все свойства этих операций были удовлетворены, как это показано на рис. 6.1.
Каждое слово — аддитивная инверсия себя. Каждое слово (кроме 00 ) имеет мультипликативную инверсию. Мультипликативные обратные пары — ( 01,01 ) и ( 10, 11 ). Сложение и умножение определено в терминах полиномиалов.
Полиномы
Хотя мы можем непосредственно определить правила для операций сложения и умножения слов из двух бит, которые удовлетворяют свойства в GF(2n), проще работать с полиномиальным степени n – 1 побитным представлением слов. Полиномиальное выражение степени n – 1 имеет форму
f(x) = an-1xn-1 + an-2xn-2 + …… + a1x1 + a0x0
где xi назван термином " i -тый элемент", а ai называется коэффициентом i - того элемента. Хотя мы знаем полиномы в алгебре, но при представлении n -битовых слов полиномами необходимо следовать некоторым правилам:
а. степень x определяет позицию бита в n -битовых слов. Это означает, что крайний левый бит находится в нулевой позиции (связан с x0 ), самый правый бит находится в позиции n–l (связан с xn-l );
b. коэффициенты сомножителей определяют значение битов. Каждый бит принимает только значение 0 или 1, поэтому наши полиномиальные коэффициенты могут иметь значение 0 или 1.
Пример 6.2
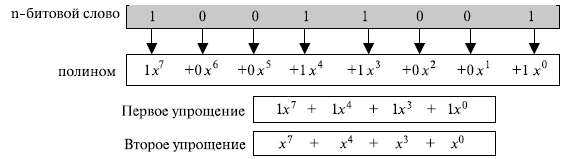
Использование полиномов для предоставления слова из 8 бит (10011001) показано на рис. 6.2.
Заметим, что элемент полностью пропущен, если его коэффициент равен 0, и пропущен только коэффициент, если это 1. Также заметим, что элемент x0 равен 1.
Пример 6.3
Чтобы найти слово на 8 битов, связанное с полиномом X5+ X2 + X, мы сначала восстановим пропущенные сомножители. Мы имеем n = 8, это означает полином степени 7. Расширенный полином имеет вид
0X7 + 0X6 + 1X5 + 0X4 + 0X3 + 1X2 + 1X1 + 0X0
Он связан со словом на 8 битов 00100110.
Операции
Обратите внимание, что любая операция на полиномах фактически включает две операции: операции И коэффициентов двух полиномов. Другими словами, мы должны определить два поля: одно для коэффициентов и одно для полиномов. Коэффициенты равны 0 или 1 ; для этой цели мы можем использовать GF(2) -поле. Мы уже говорили о таком поле (см. пример 6.1). Для полиномов нам нужно поле GF(2n), которое мы коротко обсудим ниже.
Модуль
Перед определением операций на полиномах мы должны поговорить о полиномах-модулях. Сложение двух полиномов никогда не создает полином, выходящий из множества. Однако умножение двух полиномов может создать полином со степенью большей, чем n – 1. Это означает, что мы должны делить результат на модуль и сохранять только остаток, как мы сделали в модульной арифметике. Для множеств полиномов в GF(2n) группа полиномов степени n определена как модуль. Модуль в этом случае действует как полиномиальное простое число. Это означает, что никакие полиномы множества не могут делить этот полином. Простое полиномиальное число не может быть разложено в полиномы со степенью меньшей, чем n. Такие полиномы называются неприводимые полиномы. Таблица 6.1 показывает примеры полиномов 1-5 степеней.
Для каждого значения степени часто есть более чем один неразлагаемый полином, — это означает, что когда мы определяем наш GF(2n), мы должны объявить, какой неприводимый полином мы используем как модуль.