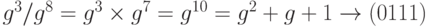|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Поля
Использование генератора
Иногда проще определить элементы поля GF(2n), используя генератор. В этом поле с неприводимым полиномом f(x) и элементом поля a нужно удовлетворить отношение f(а) = 0. В частности, если g — генератор поля, то f(g)=0. Тогда можно доказать, что элементы поля могут быть сгенерированы как
{0, g,g, g2,.... gn}, где N = 2n – 2
 |
000 (0) | 001 (1) | 010 (x) | 011 (x+1) | 100 (x2) | 101 (x2+1) | 110 (x2 + x) | 111 (x2+x+1) |
|---|---|---|---|---|---|---|---|---|
| 000 (0) | 000 (0) | 001 (1) | 010 (x) | 011 (x+1) | 100 (x2) | 101 (x2+1) | 110 (x2 + x) | 111 (x2+x+1) |
| 001 (1) | 001 (1) | 000 (0) | 011 (x+1) | 010 (x2) | 101 (x2+1) | 100 (x2+x) | 111 (x2+x+1) | 110 (x2 + x) |
| 010 (x) | 010 (x) | 011 (x+1) | 000 (0) | 001 (1) | 110 (x2 + x) | 111 (x2+x+1) | 100 (x2+x) | 101 (x2+1) |
| 011 (x+1) | 011 (x+1) | 010 (x) | 001 (1) | 000 (0) | 111 (x2+x+1) | 110 (x2 + x) | 101 (x2+1) | 100 (x2) |
| 100 (x2) | 100 (x2) | 101 (x2+1) | 110 (x2 + x) | 111 (x2+x+1) | 000 (0) | 001 (1) | 010 (x) | 011 (x+1) |
| 101 (x2+1) | 101 (x2+1) | 100 (x2) | 111 (x2+x+1) | 110 (x2 + x) | 001 (1) | 000 (0) | 011 (x+1) | 010 (x) |
| 110 (x2 + x) | 110 (x2 + x) | 111 (x2+x+1) | 100 (x2) | 101 (x2+1) | 010 (x) | 011 (x+1) | 000 (0) | 001 (1) |
| 111 (x2+x+1) | 111 (x2+x+1) | 110 (x2 + x) | 101 (x2+1) | 100 (x2) | 011 (x+1) | 010 (x) | 001 (1) | 000 (0) |
 |
000 (0) | 001 (1) | 010 (x) | 011 (x+1) | 100 (x2) | 101 (x2+1) | 110 (x2 + x) | 111 (x2+x+1) |
|---|---|---|---|---|---|---|---|---|
| 000 (0) | 000 (0) | 000 (0) | 000 (0) | 000 (0) | 000 (0) | 000 (0) | 000 (0) | 000 (0) |
| 001 (1) | 000 (0) | 001 (1) | 010 (x) | 011 (x+1) | 100 (x2) | 101 (x2+1) | 110 (x2 + x) | 111 (x2+x+1) |
| 010 (x) | 000 (0) | 010 (x) | 100 (x) | 110 (x2 + x) | 101 (x2+1) | 111 (x2+x+1) | 001 (1) | 011 (x+1) |
| 011 (x+1) | 000 (0) | 011 (x+1) | 110 (x2 + x) | 101 (x2+1) | 001 (1) | 010 (x) | 111 (x2+x+1) | 100 (x2) |
| 100 (x2) | 000 (0) | 100 (x2) | 101 (x2+1) | 001 (1) | 111 (x2+x+1) | 011 (x+1) | 010 (x) | 110 (x2 + x) |
| 101 (x2+1) | 000 (0) | 101 (x2+1) | 111 (x2+x+1) | 010 (x) | 011 (x+1) | 110 (x2 + x) | 100 (x2) | 001 (1) |
| 110 (x2 + x) | 000 (0) | 110 (x2 + x) | 001 (1) | 111 (x2+x+1) | 010 (x) | 100 (x2) | 011 (x+1) | 101 (x2+1) |
| 111 (x2+x+1) | 000 (0) | 111 (x2+x+1) | 011 (x+1) | 100 (x2) | 110 (x2 + x) | 001 (1) | 101 (x2+1) | 010 (x) |
Пример 6.11
Для генерирования элементов поля GF(24) используйте полином f(x) = x4 + x +1.
Решение
Элементы 0, g0, g 1, g2 и g3 могут быть сгенерированы достаточно просто, потому что в 4 -битовом поле они представлены 0, x0, x 1, x2 и x3 (не требуется деления на полином). Элементы от g4 до g14, которые представляют g4 до g14 от x4 до x14, нужно разделить на неприводимый полином. Для такого деления можно использовать полином f(g) = g4 + g +1 = 0. Применив это отношение, мы имеем g4 = –g–1. поскольку сложение полей и вычитание полей — та же самая операция, g4 = g + 1. Мы используем это отношение, чтобы найти значение всех элементов в виде 4 -битовых слов:
0 = 0 = 0 = 0 -> 0=(0000) g0 = g1 = g1 -> g1 = (0010) g2 = g2 = g2 -> g2 = (0100) g3 = g3 = g3 -> g3 = (1000) g4 = g4 = g + 1 -> g4 = (0011) g5 = g(g + 1) = g2 + g -> g5 = (0110) g6 = g(g2 + g) = g3 + g2 -> g6 = (1100) g7 = g(g3 + g) = g3 + g + 1 -> g7 = (1011) g8 = g(g3 + g + 1) = g2 + 1 -> g8= (0101) g9 = g(g2 + 1) = g3 + g -> g9 = (1010) g10 = g(g3 + g) = g2 + g + 1 -> g10 = (0111) g11 = g(g2 + g + 1) = g3 + g2 + g -> g11 = (1110) g12 = g(g3 + g2 + g) = g3 + g2 + g + 1 -> g12 = (1111) g13 = g(g3 + g2 + g + 1) = g3 + g2 + 1 -> g13 = (1101) g14 = g(g3 + g2 + 1) = g3 + 1 -> g14 = (1001)
Главная идея состоит в том, что вычисление элементов поля от g4 до g14 сводится к использованию соотношения g4 = g +1 и предыдущих вычислений. Например,
g12 = g(g11) =g(g3 + g2 + g) = g4 + g3 + g2 = g3 + g2 + g + 1
После сокращения можно просто преобразовать степени в n -битовое слово. Скажем, g3 + 1 эквивалентно 1001, потому что присутствуют элементы со степенью 0 и 3. Заметим, что элементы с одинаковой степенью при таком процессе вычисления отменяют друг друга. Например, g2 + g2 = 0.
Инверсии
Нахождение инверсий при использовании приведенного выше метода представления достаточно просто.
Аддитивные инверсии
Аддитивная инверсия каждого элемента — элемент непосредственно, потому что сложение и вычитание в этом поле — одна и та же операция, g3 = g3.
Мультипликативные инверсии
Найти мультипликативную инверсию каждого элемента также очень просто. Например, может найти мультипликативную инверсию элемента g3, как показано ниже:
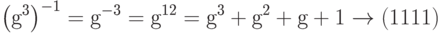
Заметим, что в этом случае степень рассчитывается по модулю 2n – 1, 24 – 1 = 15.
Поэтому –3 mod 15 = 12 mod 15.
Можно легко доказать, что g3 и g12 есть инверсные (обратные числа), потому что g3 g12 = g15 = g0 = 1.
Сложение и вычитание
Сложение и вычитание — это одинаковые операции. Промежуточные результаты могут быть упрощены, как проиллюстрировано в следующем примере.
Пример 6.12
Этот пример показывает результаты операций сложения и вычитания:
a. 
b. 
Умножение и деление
Умножение есть сложение степени по модулю 2n – 1. Деление — это умножение, которое использует мультипликативную инверсию.
Пример 6.13
Ниже показаны операции умножения и деления:
а. 
б.