Организационный инструментарий менеджмента

4.2. Сетевые графики

Сетевые графики (сетевые) модели являются мощным и гибким организационным инструментом менеджмента. Они позволяют осуществлять календарное планирование работ, оптимизацию использования ресурсов, сокращать продолжительность выполнения работ в зависимости от их стоимости или же увеличивать продолжительность исходя из бюджетных ограничений, организовывать оперативный менеджмент в ходе реализации деятельности. Сетевые графики занимают важнейшее место в современном проектном менеджменте.

Сетевой график представляет собой ориентированный граф (геометрическую фигуру, состоящую из вершин и направленных стрелок), изображающий все необходимые для достижения цели операции в их технологической взаимосвязи.

Основными понятиями сетевой модели являются:

• работа;
• событие;
• путь.

Работа - это трудовой процесс, требующий затрат времени и ресурсов. В модели работа изображается в виде сплошной стрелки (дуги графа), над которой стоит цифра, показывающая ее продолжительность. Работа идентифицируется номерами начального и конечного события. Иногда в более сложных сетевых моделях допускается нанесение (сверху или снизу от стрелки) и других условных изображений, таких как наименование работы, ее стоимость, объем, исполнителя, продолжительности, количества ресурсов. С другой стороны, иногда используются модели без каких-либо числовых показателей и обозначений. Такая сеть называется структурной сетевой моделью, или топологией.

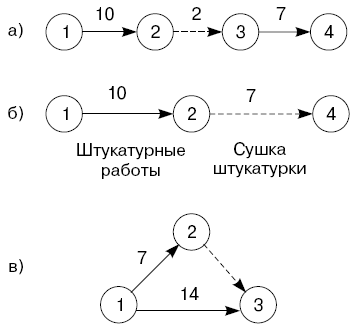
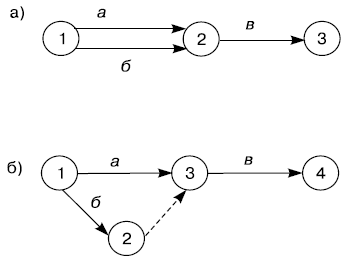
Рис. 4.1. Изображение на сетевом графике: а - работы и ожидания; б - технологического ожидания; в - зависимости событий

В понятие "работа" включается "процесс ожидания", т.е. процесс, не требующий затрат труда, но требующий затрат времени. Обычно ожидание изображают в виде пунктирной стрелки, над которой указывают продолжительность ожидания ( рис. 4.1 а, б).

Понятие работы учитывает "зависимость" между двумя или несколькими событиями, не требующую затрат времени, ресурсов, но показывающую логическую связь работ, например, что начало одной или нескольких работ зависит от результатов другой работы. На графике зависимость (или как часто ее не совсем правильно называют "фиктивная работа") показывается в виде пунктирной стрелки без указания времени.

Зависимость используется в сетевых графиках не только как технологическая или организационная связь, но и как элемент, необходимый для выполнения определенных правил построения сетевых графиков.

Событие - это результат выполнения одной или нескольких работ, позволяющий начинать другую работу. В сетевых моделях событие изображается, как правило, в виде кружка.

События не являются процессами и не имеют длительности, т.е. совершаются мгновенно. Поэтому каждое событие, включаемое в график, должно быть полно, точно и всесторонне определено (с точки зрения логической связи работ), его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.

Событие, стоящее в начале сетевого графика, в которое не входит ни одной работы, называется исходным событием. Событие, стоящее в конце сетевого графика, из которого не выходит ни одной работы, называется завершающим событием.

События делятся на простые и сложные. Простые события - это те, в которые входит одна работа. Сложные события - это те, в которых соединяются две или более работ.

Рис. 4.2. Изображение события на сетевом графике

Событие может являться частным результатом отдельной работы или же суммарным результатом нескольких работ. Событие может совершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только после того, как произойдет это событие. Отсюда двойственный характер событий (кроме исходного и завершающего): для всех непосредственно предшествующих событию работ оно является конечным, а для всех непосредственно следующих за ним - начальным ( рис. 4.2).

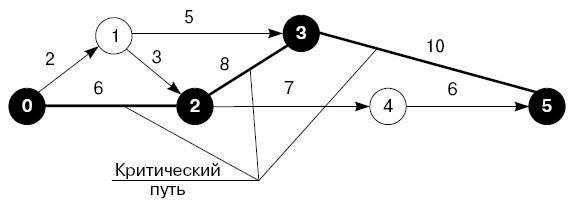
Путь - это непрерывная последовательность стрелок, начиная от исходного события сетевой модели и заканчивая завершающим. Длина пути определяется продолжительностью работ, лежащих на этом пути.

При сравнении продолжительности путей выявляется путь, длина которого (суммарная продолжительность работ на этом пути) имеет наибольшую величину по сравнению с длиной любого другого пути. Такой путь называется критическим. Критический путь определяет общую продолжительность работ. Пример выявления критического пути изображен на рис. 4.3. Изображенный на рисунке сетевой график имеет пять путей.

Рис. 4.3. Графическое обозначение пути на сетевом графике

При контроле работ, выполняемых по сетевому графику, главное внимание концентрируется на работах критического пути, так как именно от них зависит выполнение всех работ в установленный срок. Совершенно естественно, что для сокращения общей продолжительности работ надо искать возможности ускорения работ, лежащих на критическом пути.

Работы, лежащие на критическом пути, являются потенциально "узкими местами". Поэтому внимание руководителя должно сосредоточиваться именно на этих работах. А так как критический путь имеет самую большую продолжительность по сравнению с другими путями, то эти последние имеют запас времени, что дает возможность оперативно маневрировать ресурсами или снижать стоимость выполнения работ за счет увеличения их продолжительности.

Как показывает практика, чем больше работ включает сетевой график, тем меньше удельный вес работ, лежащих на критическом пути. Например, в модели со 100 работами на критическом пути будут находиться 10-12% от общего количества работ; при 1000 работ - 7-8%; при 5000 работ - 3-4%.

Правила построения сетевых моделей

Единой принятой последовательности составления сетевого графика нет. Поэтому строить графики можно по-разному - от начала и до окончания, а также и наоборот - от конца к началу. Более логичным и правильным следует признать метод построения графиков от исходного события до завершающего, т.е. слева направо, так как при таком построении четко понимается технология выполнения моделируемых работ. Этот метод получил наибольшее признание.

Поэтому в качестве первого правила последовательности отображения работ следует указать, что сетевые графики следует строить от начала к окончанию, т.е. слева направо.

Правило изображения стрелок. Стрелки, изображающие работы, ожидания или зависимости, могут иметь различный наклон и длину, но должны, как правило, идти слева направо. Стрелки в сетевом графике не должны отклоняться влево от оси ординат. И конечно, следует иметь в виду, что стрелки направляются всегда от предшествующих событий к последующим, от событий с меньшими номерами к событиям с большими номерами.

Правило пересечения стрелок. Пересечения стрелок допустимы, но чем меньше пересечений, тем график более продуман и нагляден.

Изложенные три правила можно рассматривать как предварительные. Теперь перейдем к основным правилам построения сетевых графиков.

Правило обозначения работ. В практике зачастую встречаются случаи, когда две и более работ выходят из одного и того же события, выполняются параллельно и заканчиваются одним и тем же событием.

Например, одновременно начинается проектирование двух вариантов конструкции новой машины. После их разработки проводится сопоставление и выбор лучшего варианта.

Но правильное изображение этих работ на сетевом графике не должно выводить две работы из одного события и завершать их одним тем же событием. При таком изображении обе работы получают одно и то же обозначение, а это недопустимо, так как при расчете сети невозможно будет определить параметры этих работ, да и всего сетевого графика ( рис. 4.4 а).

В сетевом графике между двумя смежными событиями может проходить только одна стрелка. Обычно для распараллеливания работ вводят дополнительное событие, что показано на рис. 4.4 б.

Рис. 4.4. Изображение на сетевом графике параллельных работ: а) неправильное; б) правильное

Правило расчленения и запараллеливания работ. Во многих процессах позволяется начинать следующую работу, не ожидая полного окончания предшествующей. В этом случае производится "расчленение" предшествующей работы.

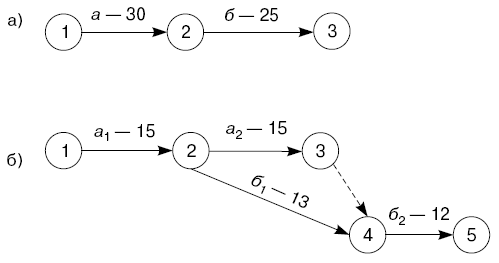
Рис. 4.5. Построение сетевого графика: а) последовательные работы; б) расчленение и запараллеливание работ

На графике вводится дополнительное событие в том месте предшествующей работы, где может начаться новая. Пример этого приведен на рис. 4.5. Предстоящая работа предполагает необходимость корректировать рабочие чертежи (работа "а", продолжительность 30 дней) и изготовить испытательный стенд (работа "б", продолжительность 25 дней). Если эти работы изобразить последовательно, то общая продолжительность составит 55 дней, как это изображено на рис. 4.5 а, между работами. После составления сетевого графика и анализа взаимосвязи предполагается, что работу "б" можно начать после выполнения половины работы "а", т.е. через 15 дней. Закончить работу "б" можно только после полного окончания работы "а". Исходя из этого можно построить новый сетевой график, изображенный на рис. 4.5 б. Из него видно, что общая продолжительность работ теперь составляет 42 дня, т.е. мы получили выигрыш во времени на 13 дней.

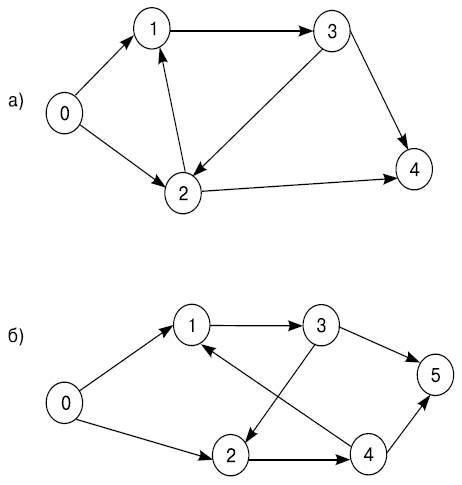
Правило запрещения замкнутых контуров (циклов или петель). При построении сети недопустимо строить замкнутые контуры, т.е. пути, в которых некоторые события соединяются сами с собой. Нельзя допустить, чтобы в сети возник случай, когда один и тот же путь ведет к тому же событию, из которого он первоначально вышел. Различные случаи замкнутых контуров изображены на рис. 4.6 а, б.

Рис. 4.6. Запрещенные замкнутые контуры: а) петля (1-3-2-1); б) «восьмерка» (1-3-2-4-1)

Если такое замыкание произошло, то это означает, что имеются ошибки в технологии или в составлении графика.

Правило запрещения "тупиков". В сетевом графике не должно быть тупиков - событий, из которых не выходит ни одной работы, за исключением завершающего события (в многоцелевых графиках завершающих событий несколько, но это особый случай).

Правило запрещения "хвостовых" событий. В сетевом графике не должно быть хвостовых событий, т.е. событий, в которые не входит ни одной работы, если это событие не является начальным.

Правила запрещения "тупиков" и "хвостовых" событий проиллюстрированы на рис. 4.7.

Рис. 4.7. Запрещенные события сетевого графика: а) «тупик» (4); б) «хвостовое» (1)

Правила изображения дифференцированно-зависимых работ. В практике построения сетевых графиков постоянно встречаются случаи, когда одна группа работ зависит от другой группы, а одна или несколько работ имеют дополнительные зависимости или ограничения. Обычно для решения этой проблемы вводят дополнительные события, как это показано на рис. 4.8.

Рассмотрим две группы работ - "а", "б", "в" и "г", "д", "е", изображенные на рис. 4.8 а. Представим, что существует следующая зависимость между этими группами: работа "г" зависит от работ "б" и "в", а работа "д" зависит только от работы "б".

Сам собой напрашивающийся вариант сетевой модели, объединяющий обе группы работ, приведен на рис. 4.8 б.

Но такой вариант неправильный. Так как сетевой график показывает, что работа "д" зависит как от работы "б", так и от работы "в", а это противоречит исходной моделируемой технологии.

Чтобы построить правильную сетевую модель, необходимо ввести дополнительное событие.

Правильный сетевой график показан на рис. 4.8 в. Здесь видим, что работы "г" и "д", являющиеся дифференцированно-зависимыми, имеют каждая свою зависимость от предшествующих работ.

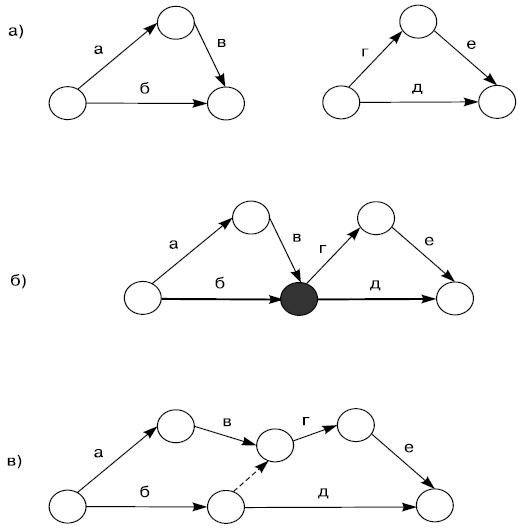
Рис. 4.8. Изображение дифференцированно-зависимых работ: а) исходная ситуация; б) неправильное построение; в) правильное построение

Правило учета непосредственных примыканий (зависимостей). В сетевом графике учитывается только непосредственное примыкание (зависимость) между работами ( рис. 4.9).

Рис. 4.9. Изображение непосредственных примыканий (зависимостей) сетевого графика

Исходя из сетевого графика на рисунке, можно сказать, что работе "г" предшествует только работа "в". Если нужно показать, например, что работе "г" предшествует также и работа "а", то это надо сделать специально вводимой зависимостью.

Правило кодирования событий сетевого графика. Для кодирования сетевых графиков необходимо руководствоваться следующими требованиями:

1. все события графика имеют самостоятельные номера;
2. кодируются события числами натурального ряда без пропусков;
3. номер последующему событию присваивается после присвоения номеров предшествующим событиям;
4. стрелка (работа) должна быть всегда направлена из события с меньшим номером в событие с большим номером.

Последовательность проставления цифр в событиях указана в самой нумерации событий и определена направленностью стрелок.

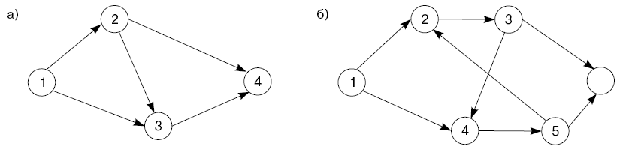
Четкая система кодирования позволяет выявить имеющиеся в сети замкнутые контуры.

Правила кодирования событий сетевого графика проиллюстрированы на рис. 4.10.

увеличить изображение
Рис. 4.10. Кодирование событий сетевого графика: а) правильное; б) неправильное (замкнутый контур)