Системы представления знаний

Нечеткая логика

При формализации знаний достаточно часто встречаются качественные знания, например, высокая температура при гриппе, слабое свечение нити накаливания, молодой дипломат и т.д. Для формального представления таких качественных знаний американский математик, профессор информатики в Университете в Беркли (Калифорния) Лофти А.Заде (Иран) предложил в 1965 году формальный аппарат нечеткой (fuzzy) логики [ 2.8 ] .

Нечеткое подмножество N множества M определяется как множество упорядоченных пар }, где - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значения в интервале [0, 1] и указывающая степень (или уровень) принадлежности элемента x подмножеству N. Таким образом, нечеткое множество N можно записать как

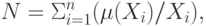
где X_i - i -е значение базовой шкалы, а знак " + " не является обозначением операции сложения, а имеет смысл объединения.

Определим лингвистическую переменную (ЛП) как переменную, значение которой определяется набором словесных характеристик некоторого свойства. Например, ЛП "возраст" может иметь значения

ЛП = МлВ, ДВ, ОВ, ЮВ, МВ, ЗВ, ПВ, СВ ,

обозначающие возраст младенческий, детский, отроческий, юношеский, молодой, зрелый, преклонный и старый, соответственно. Множество M - это шкала прожитых человеком лет [0..120]. Функция принадлежности определяет, насколько мы уверены, что данное количество прожитых лет можно отнести к данному значению ЛП. Допустим, что неким экспертом к молодому возрасту отнесены люди в возрасте 20 лет со степенью уверенности 0,8, в возрасте 25 лет со степенью уверенности 0,95, в возрасте 30 лет со степенью уверенности 0,95 и в возрасте 35 лет со степенью уверенности 0,7. Итак:

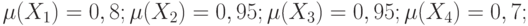
Значение ЛП=МВ можно записать:

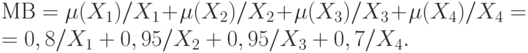
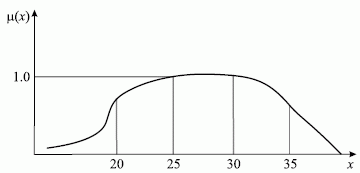
Таким образом, нечеткие множества позволяют учитывать субъективные мнения отдельных экспертов. Для большей наглядности покажем множество МВ графически при помощи функции принадлежности ( рис. 2.7).

Рис. 2.7. График функции принадлежности

Для операций с нечеткими множествами существуют различные операции, например, операция "нечеткое ИЛИ" (иначе ) задается в логике Заде [ 2.9 ] , [ 2.10 ] :

и при вероятностном подходе так:

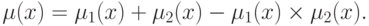
Существуют и другие операции над нечеткими числами, такие как расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел, определяемые через соответствующие операции для четких чисел с использованием принципа обобщения и т.д.

Как мы увидим в дальнейшем, нечеткие множества (другое название - мягкие вычисления) очень часто применяются в экспертных системах. Нечеткая логика применяется как удобный инструмент для управления технологическими и индустриальными процессами, для интеллектуального домашнего хозяйства и электроники развлечения, в системах обнаружения ошибок и других экспертных системах. Разработаны специальные средства нечеткого вывода, например, инструментальное средство Fuzzy CLIPS. Нечеткая логика была изобретена в Соединенных Штатах, и сейчас быстрый рост этой технологии начался в Японии, Европе и теперь снова достиг США.

Развитием этого направления является реализации в системах представления знаний НЕ-факторов: неполнота, неточность, недоопределенность, неоднозначность, некорректность и др. [ 2.11 ] .

Завершая лекцию по СПЗ, следует отметить следующее. Системы представления знаний и технологии работы со знаниями продолжают развиваться. Читатель может самостоятельно познакомиться с новым языком описания декларативных знаний (ЯОДЗ) и технологией функционально-ориентированного проектирования (ФОП-технологией) для решения информационно-сложных задач в работах [ 2.12 ] , [ 2.13 ] .

Кроме традиционных языков (LISP, PROLOG, SMALLTALK, РЕФАЛ) и инструментальных средств (LOOPS, KEE, ART) для представления знаний в настоящее время появляются новые веб-ориентированные версии ИС [ 2.14 ] . Весьма популярными стали средства на базе JAVA: системы Exsys Corvid, JESS. Язык HTML явился основой для представления знаний в среде Интернет [ 1.2 ] . С такими современными средствами, как система G2 и система CLIPS, читатель сможет познакомиться в лекциях 6 и 7.