Интеллектуальная система управления робота-станка

Основными требованиями к системам управления технологическими машинами, построенными на подвижных стержневых механизмах, являются, во-первых, обеспечение технологических режимов для выполняемой операции, точности и качества получения поверхности при ее обработке и, во-вторых, выполнение указанных требований при наличии упругих деформаций исполнительных механизмов. Это возможно только в том случае, если работает система контроля технологических параметров, геометрических размеров обрабатываемой поверхности, положения исполнительных механизмов и упругих передвижений звеньев манипуляторов перемещения инструмента и изделия. Указанные системы контроля оснащаются датчиками контроля положения звеньев механизма, упругих перемещений, режимов обработки (датчики измерения силы резания, подачи, скорости резания, износа инструмента и др.), качества обрабатываемой поверхности и ее геометрических размеров.

Система управления технологической машиной.

Система управления технологической машиной (рис. 8.2) в целом представляет сложную систему, способную решать отдельные интеллектуальные задачи. Как правило, современное производство еще далеко от того, чтобы широко применять указанные системы. Поэтому в данной лекции мы попытаемся рассмотреть только отдельные интеллектуальные задачи, решаемые системой управления станочного оборудования, построенного на подвижных стержневых механизмах. Указанные системы по своим функциональным характеристикам близки к промышленным роботам и во многом на них похожи.

Система управления, представленная на рисунке 8.3, предназначена для формирования законов управления исполнительными приводами, обработки информации систем контроля, задания траектории перемещения инструмента относительно обрабатываемой детали и обеспечения требуемых режимов обработки. Рассмотрим основные функции, выполняемые данной системой (рис. 10.1), более детально.

Рис. 10.1.

1. Описание поверхности, которую требуется получить после обработки на каждом переходе, а также после окончательной обработки. Эта информация хранится в виде массива опорных точек поверхности.
2. Формирование траектории движения инструмента. Траектория рассчитывается исходя из снимаемого припуска на каждом переходе как непрерывное перемещение подвижного трехгранника ^ДA_i в системе координат детали.
3. Сравнение программной траектории перемещения инструмента ^ДA_i с реальным его положением ^ДA_K в системе координат детали. На основе данного сравнения определяются погрешности линейных и угловых координат
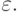
4. Определение реальных координат заготовки. Оптическая система контроля поверхности определяет реальные координаты поверхности заготовки A_Д^* в системе координат детали. Сравнивая реальные координаты A_Д^* с идеальными A_Д формируется массив распределения припуска по обрабатываемой поверхности.
5. Вторым функциональным предназначением оптической системы контроля является определение шероховатости обрабатываемой поверхности и ее распределение. В зависимости от дискретной градации уровня шероховатости формируются зоны S_i на поверхности с заданным уровнем микронеровностей R_Z.
6. Выбор информационных датчиков контроля положения. Информационные датчики q_инф. выбираются из суммарного количества датчиков q_m+q_i, определяющих перемещения в сочленениях звеньев механизма параллельной структуры. Критерием, по которому выбираются данные датчики, является минимум погрешности вычисления выходного звена при заданной погрешности датчиков.

Состав системы управления и функциональные характеристики ее элементов. В состав системы управления (рис. 10.1) входят сепаратные приводы, представляющие замкнутые по положению следящие системы по каждой управляемой координате механизма. Кроме этого, система управления в целом также представляет следящую систему, в которой осуществляется сравнение программного положения режущей кромки инструмента ^ДA_i с реальным его положением ^ДA_K в системе координат детали.

Как было отмечено в лекции 9, для описания математических преобразований используется аппарат однородных матричных преобразований. Положение подвижного трехгранника 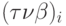, определяющего программное положение режущей кромки (рис. 10.2) в каждый момент времени, задается матрицей

где

- подматрица направляющих косинусов осей подвижного трехгранника 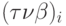, определяющего программное положение режущей кромки относительно осей координатной системы (XYZ)_Д ;

^ДR_i =[x_iy_iz_i]^T - вектор, определяющий программное положение i-й точки поверхности в системе координат (XYZ)_Д.

Соответственно, реальное положение режущей кромки определяется матрицей, аналогичной (10.1)

Рис. 10.2.

В соответствии с (10.2), рассогласование между программным ^KA_i и реальным положениями режущей кромки ^ДA_K определяется из матричного произведения

ДAi=ДAKKAi, (10.3)

из которого

KAi=(ДAK)-1ДAi. (10.4)

Рассогласование между положениями трехгранников представляется матрицей ^KA_i, структурно аналогичной матрицам (10.1) и (10.2). На основе ^KA_i формируется вектор 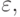элементами которого являются три элемента четвертого столбца, определяющие линейное рассогласование, и три элемента из матрицы направляющих косинусов ^KA_i, не принадлежащие одному столбцу и одной строке. Вектор является исходным для вычисления приращений управляющих обобщенных координат .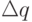

Обратное преобразование Якоби J^-1 (рис. 8.3), представляющее обратное преобразование от матрицы

связывает погрешности положения инструмента и приращения обобщенных управляемых координат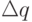

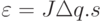( 10.5)

Система линейных уравнений (10.5) решается относительно 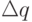любым известным методом.

Выбор добротности и корректирующих устройств, обеспечивающих устойчивость системы и требуемую точность 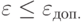, осуществляется настройкой коэффициентов усиления K (рис. 8.3). Для определения начального положения механизма q_i необходимо решать обратную задачу F^-1(q) в абсолютных координатах.

Описание сложной поверхности и планирование управления исполнительными приводами для ее воспроизведения рассматривается в лекции 11.

Дополнительные датчики при решении прямой и обратной задач кинематики.

Решение прямой и обратной задач кинематики подвижных стержневых механизмов параллельной структуры осуществляется с использованием дополнительных датчиков. Для этого датчики положения устанавливаются в сочленениях звеньев, содержащих и не содержащих исполнительные приводы. Это позволяет оперативно вычислять управление исполнительными приводами и сокращает вычислительные ресурсы. Однако при этом необходимо решать задачу выбора группы датчиков для соответствующей конфигурации механизма, которые с наибольшей точностью определяют положение его выходного звена. Например, два датчика (рис. 10.3), имеющие одинаковую погрешность определения углового положения 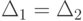с разной точностью определяют линейные перемещения в направлении оси X. Датчик D1 определяет значение X более точно, чем D2, и 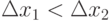. При другом положении точки i на плоскости значимость точности датчика может поменяться.

Рис. 10.3.

Манипулятор перемещения изделия специального робота-станка для обработки пера лопаток (рис. 8.1) содержит дополнительные датчики. Данный манипулятор имеет четыре управляемых двигателя D1, D2, D3, D4 для перемещения выходного звена (платформы П) по четырем координатам: двум линейным и двум угловым (рис. 10.4). Кроме датчиков контроля углов поворота двигателей q₁, q₂, q₃ и q₄, в механизме установлены датчики измерения углов взаимного положения звеньев, расположенные в сочленениях , , .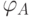

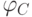Рис. 10.4.

Для определения положения платформы П относительно базовой системы координат (XYZ)₀ достаточно знать длины звеньев 1—6 ( L₁—L₆ ) и четыре угла поворота. При наличии семи датчиков контроля углового положения звеньев q₁, q₂, q₃, q₄, 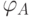, , 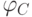требуется найти такое сочетание четырех из семи ⁴C₇ информационных углов, которое обеспечит минимальную погрешность определения координат выходного звена (XY) относительно (XYZ)₀. Решение данной задачи в общем случае рассмотрено в лекции 13.