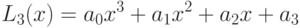НОУ ИНТУИТ | Введение в математическое моделирование. Лекция 11: Компьютерное моделирование при обработке опытных данных

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 15.03.2007 | Уровень: специалист | Доступ: свободно | ВУЗ: Донецкий национальный технический университет

Вам нравится? Нравится 69 студентам

| Поделиться |

Поддержать программу

Программирование формулы Ньютона

Для построения многочлена Ньютона по формуле (11.7) организуем циклический вычислительный процесс по 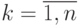$k=\overline{1,n}$ . При этом на каждом шаге поиска находим разделенные разности k -го порядка. Будем помещать разделенные разности на каждом шаге в массив Y.

Тогда рекуррентная формула (11.8) будет иметь вид:

$y_i = \frac{y_{i+1} - y_i}{x_{i+k} - x_i}\\ k=\overline{1,n};\\ i=\overline{0,n-k}.$

( 11.9)

В формуле Ньютона (11.7) используются разделенные разности k -го порядка, подсчитанные только для участков [x₀, x_0+k], т.е. разделенные разности k -го порядка для i=0. Обозначим эти разделенные разности k-го порядка как у₀. А разделенные разности, подсчитанные для I > 0, используются для расчетов разделенных разностей более высоких порядков.

Используя (11.9), свернем формулу (11.7). В результате получим

$L_n(x) = y_o + \sum \limits_{k=1}^{n}P \cdot y_0^*$

( 11.10)

где

у₀ - значение табличной функции (11.1) для x=x₀.

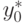y_0^* - разделенная разность k-го порядка для участка [x₀, x_0+k].

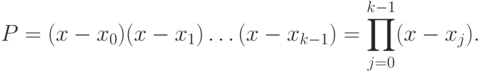
$P = (x - x_0)(x - x_1)\ldots (x - x_{k-1}) = \prod \limits_{j=0}^{k-1} (x - x_j).$

Для вычисления Р удобно использовать рекуррентную формулу P = P(x - x_k-1) внутри цикла по k.

Схема алгоритма интерполяции по Ньютону представлена на рис.11.4.

Рис. 11.4. Схема алгоритма интерполяции по Ньютону

Пример интерполяции по Ньютону

Дана табличная функция:

i	x_i	y_i
0	2	0,693147
1	3	1,098613
2	4	1,386295
3	5	1,609438

Вычислить разделенные разности 1-го, 2-го, 3-го порядков (n=3) и занести их в диагональную таблицу.

Разделенные разности первого порядка:

$f(x_0,x_1) = \frac{f(x_1) - f(x_0)}{x_1 - x_0}= \frac{1,098613 - 0,693147}{3 - 2} = 0,405466.\\ f(x_1,x_2) = \frac{f(x_2) - f(x_1)}{x_2 - x_1}= \frac{1,386295 - 1,098613}{4 - 3} = 0,287682.\\ f(x_2,x_3) = \frac{f(x_3) - f(x_2)}{x_3 - x_2}= \frac{1,609438 - 1,386295}{5 - 4} = 0,223143.$

Разделенные разности второго порядка:

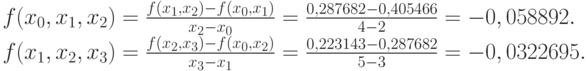
$f(x_0,x_1,x_2) = \frac{f(x_1,x_2) - f(x_0,x_1)}{x_2 - x_0}= \frac {0,287682 - 0,405466}{4 - 2} = -0,058892.\\ f(x_1,x_2,x_3) = \frac{f(x_2,x_3) - f(x_0,x_2)}{x_3 - x_1}= \frac {0,223143 - 0,287682}{5 - 3} = - 0,0322695.$

Разделенная разность третьего порядка:

$f(x_0,x_1,x_2,x_3) = \frac{f(x_1,x_3) - f(x_0,x_2)}{x_3 - x_0}= \frac {- 0,0322695 - (- 0,058892)}{5 - 2} = 0,00887416$

Таблица 11.1. Диагональная таблица разделенных разностей
i	x_i	Разделенная разность
i	x_i	0-го пор.	1-го пор.	2-го пор.	3-го пор.
0	2	0,693147
			0,405466
1	3	1,098613		-0,058892
			0,287682		0,00887416
2	4	1,386295		-0,0322695
			0,223143
3	5	1,60943

Интерполяционный многочлен Ньютона для заданной табличной функции имеет вид:

$L_3(x) = f(x_0) + (x - x_0) \cdot f(x_0,x_1) + (x-x_0)(x - x_1) \cdot f(x_0,x_1,x_2) +\\+ (x - x_0)(x - x_1)(x - x_2) \cdot f(x_0,x_1,x_2,x_3) = 0,693147 + (x - 2) \cdot 0,405466+\\ + (x-2)(x-3) \cdot (-0,058892) + (x-2)(x-3)(x-4) \cdot 0,0887416.$

Далее полученный интерполяционный многочлен Ньютона можно привести к нормальному виду

и использовать его для решения задач интерполирования или прогноза.

Дальше >>

Введение в математическое моделирование

Компьютерное моделирование при обработке опытных данных

Программирование формулы Ньютона

Пример интерполяции по Ньютону

Вопросы и ответы

Студенты

Авторизоваться

Введение в математическое моделирование

Компьютерное моделирование при обработке опытных данных

Программирование формулы Ньютона

Пример интерполяции по Ньютону

Вопросы и ответы

Студенты