|
В уравнениях движения кривошипно-шатунного механизма вместо обозначения радиуса кривошипа "r" ошибочно записан символ "?" (гамма). P.S. Может быть это слишком очевидно, но не упомянуто, что угол поворота кривошипа ? считается малым. |
Компьютерное моделирование при обработке опытных данных
Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем.
Например: зависимость числа оборотов двигателя от нагрузки, т.е. n=f(Мкр.) ; зависимость силы резания при обработке детали на металлорежущем станке от глубины резания, т.е. P=f(t), и т.д.
Из всех способов задания зависимостей наиболее удобным является аналитический способ задания зависимости в виде функции n=f(Мкр.), P=f(t), y=f(t).
Однако на практике специалист чаще всего получает зависимости между исследуемыми параметрами экспериментально. В этом случае ставится натурный эксперимент, изменяются значения параметров на входе системы, измеряются значения параметров на выходе системы. Результаты измерений заносятся в таблицу.
Таким образом, в результате проведения натурного эксперимента получаем зависимости между исследуемыми параметрами в виде таблицы, т.е. получаем, так называемую, табличную функцию.
Далее с этой табличной функцией необходимо вести научно-исследовательские расчеты. Например, необходимо проинтегрировать или продифференцировать табличную функцию и т.д.
Рассмотрим две задачи по обработке опытных данных:
Интерполирование функций
Дана табличная функция, т.е. дана таблица, в которой для некоторых дискретных значений аргумента xi, расположенных в порядке возрастания, заданы соответствующие значения функции уi:
 |
( 11.1) |
Точки с координатами (xi, yi) называются узловыми точками или узлами.
Количество узлов в табличной функции равно
N=n+1.
На графике табличная функция представляется в виде совокупности узловых точек (рис. 11.1).
Длина участка [x0, xn] равна (xn - x0).
В расчетной практике инженера часто возникают задачи найти значение функции для аргументов, которые отсутствуют в таблице. Такие задачи называются задачами интерполирования или экстраполирования.
Задача интерполирования функции (или задача интерполяции) состоит в том, чтобы найти значения yk табличной функции в любой промежуточной точке хк, расположенной внутри интервала [x0, xn], т.е.

и
![x_k \in[x_0, x_n].](/sites/default/files/tex_cache/101a8b6f2dda52713fe7b0cfd6824cd3.png)
Задача экстраполирования функции (или задача экстраполяции) состоит в том, чтобы найти значения yl табличной функции в точке хl, которая не входит в интервал [x0, xn], т.е.

Такую задачу часто называют задачей прогноза.
Обе эти задачи решаются при помощи нахождения аналитического выражения некоторой вспомогательной функции F(x), которая приближала бы заданную табличную функцию, т.е. в узловых точках принимала бы значение табличных функций

Для определенности задачи искомую функцию F(x) будем искать из класса алгебраических многочленов:
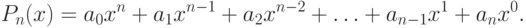 |
( 11.2) |
Этот многочлен должен пройти через все узловые точки, т.е.
 |
( 11.3) |
Поэтому степень многочлена n зависит от количества узловых точек N и равна количеству узловых точек минус один, т.е. n=N-1.
Многочлен вида (11.2), который проходит через все узловые точки табличной функции называется интерполяционным многочленом.
Интерполирование с помощью алгебраических многочленов называется параболическим интерполированием.
Таким образом, для решения задачи интерполирования прежде всего необходимо решить задачу, которую можно сформулировать следующим образом:
для функции  , заданной таблично, построить интерполяционный многочлен степени n, который проходит через все узловые точки таблицы:
, заданной таблично, построить интерполяционный многочлен степени n, который проходит через все узловые точки таблицы:

где
n -степень многочлена, равная количеству узловых точек N минус один,т.е. n=N-1.
В результате, в любой другой промежуточной точке хk, расположенной внутри отрезка [x0,xn] выполняется приближенное равенство Pn(xk) = f(xk) = yk. (рис.11.2)


