Принцип взаимосвязи
Война на истощение
Теорема 11.1 позволила нам классифицировать многие известные нам аукционы. Но в ней заложено важное ограничение: мы потребовали, чтобы в аукционе что-то платил исключительно победитель. А в реальной жизни это далеко не всегда так: мы в разделе "Теорема об эквивалентности доходности" уже приводили пример с лоббированием и получающимся в результате аукционом, в котором платят все участники. Давайте начнем подбираться к нужному обобщению принципа взаимосвязи с конкретного примера, который имеет еще и биологическую мотивацию.
В качестве этого примера мы рассмотрим так называемую войну на истощение (war of attrition). Ее можно понимать следующим образом: агенты соперничают за ресурс ценностью  , просто оставаясь в игре и терпя со временем все большие и большие убытки. Как только все агенты, кроме одного, уйдут из игры, игра закончится, и оставшийся будет объявлен победителем. Эту модель начал рассматривать упоминавшийся уже Джон Майнард Смит [45], который применил теорию игр к биологии. Модель войны на истощение — это классическая модель войны между биологическими видами за тот или иной ресурс. Виды сражаются и терпят потери, пока один из них не отступится или не вымрет полностью, после чего второй получает искомый ресурс.
, просто оставаясь в игре и терпя со временем все большие и большие убытки. Как только все агенты, кроме одного, уйдут из игры, игра закончится, и оставшийся будет объявлен победителем. Эту модель начал рассматривать упоминавшийся уже Джон Майнард Смит [45], который применил теорию игр к биологии. Модель войны на истощение — это классическая модель войны между биологическими видами за тот или иной ресурс. Виды сражаются и терпят потери, пока один из них не отступится или не вымрет полностью, после чего второй получает искомый ресурс.
Войну на истощение можно рассматривать как игру, в которой все игроки делают ставки (ставку  надо понимать как "я буду держаться, пока не понесу убытки
надо понимать как "я буду держаться, пока не понесу убытки  "), после чего выигрывает тот, у кого ставка больше, но платит он при этом вторую сверху ставку. Получается интересная форма аукциона — аукцион второй цены, в котором платят все, но победитель — не свою ставку, а вторую сверху.
"), после чего выигрывает тот, у кого ставка больше, но платит он при этом вторую сверху ставку. Получается интересная форма аукциона — аукцион второй цены, в котором платят все, но победитель — не свою ставку, а вторую сверху.
С точки зрения теории игр война на истощение — крайне интересный объект. Если не ограничивать сверху возможные ставки, у участников может возникнуть мотивация ставить больше, чем стоит объект (ведь платят они не свою ставку, а вторую). Но если этой мотивации поддадутся все игроки, то, конечно, даже победитель останется в минусе. У войны на истощение очень интересная эволюционно стабильная стратегия, суть которой такова: ставить настолько случайно, чтобы противник не смог никак предсказать последующие ставки. Мы, правда, не будем в это углубляться, а заинтересованному читателю порекомендуем [10,11,45,47].
А мы возьмемся за войну на истощение как за аукцион (как Кришна и Морган [36]). Такой вот all-pay second price auction, в котором доходы участников по вектору ставок  определяются как
определяются как
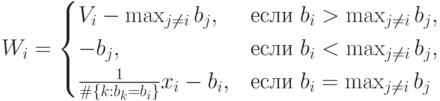
(мы будем предполагать, что в случае равенства ресурс делится поровну).
Начнем, как водится, с того, что попытаемся вывести равновесную стратегию, а затем уже докажем, что она равновесная. Предположим, что игроки следуют симметричной равновесной стратегии  , и игрок 1 получает сигнал
, и игрок 1 получает сигнал  и ставит
и ставит 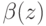 . Тогда его ожидаемый доход равен
. Тогда его ожидаемый доход равен
![W_i(z, x) = \int_{-\infty}^z\left(\mathbf E\left[\vphantom{1^2}V_1\mid X_1=x, Y_1=y\right] - \beta(y)\right)g(y|x)dy - \\ - \left(\vphantom{1^2}1 - G(z|x)\right)\beta(z) = \\ = \int_{-\infty}^z\left(\vphantom{1^2}v(x,y) - \beta(y)\right)g(y|x)dy - \left(\vphantom{1^2}1 - G(z|x)\right)\beta(z).](/sites/default/files/tex_cache/1e722a2f72251abbd2474de764fccecb.png)
Теперь максимизируем  по
по  . Это даст нам условие
. Это даст нам условие
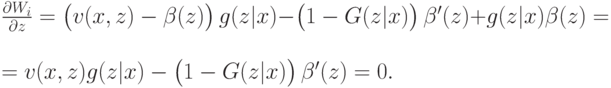
В симметричном равновесии 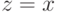 , и поэтому в равновесии условие превращается в
, и поэтому в равновесии условие превращается в

и, наконец,

если вспомнить определение доли риска  .
.
Итак, мы получили кандидата на равновесную стратегию. Осталось только доказать, что это действительно она. Это будет верно не всегда, а при дополнительном условии.
Теорема 11.2. Предположим, что для всех  функция
функция
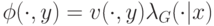
возрастает. Тогда стратегия

является симметричной равновесной стратегией для войны на истощение.
Доказательство. Доказательство будет очень похоже на кучу доказательств, которые мы уже видели. Здесь мы его еще проведем, а в 11.5 уже не будем. Итак, мы хотим доказать, что функция 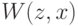 максимизируется при
максимизируется при 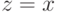 . Как мы уже знаем,
. Как мы уже знаем,

Давайте возьмем вторую часть интеграла по частям:

Но мы знаем, что
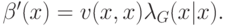
Таким образом,

Поскольку мы предположили, что  возрастает по первому аргументу, разность
возрастает по первому аргументу, разность

больше нуля для всех 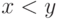 и меньше нуля для всех
и меньше нуля для всех  . Таким образом,
. Таким образом, 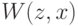 достигает максимума в точке
достигает максимума в точке 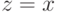 .
.
У нас получилась очень интересная стратегия. Во-первых, в нуле агент, играющий по этой стратегии, ставит ноль: мы считаем, что сигналы распределены на интервале ![[0,\omega]](/sites/default/files/tex_cache/fc0e1283428eb31676bdded9703922c5.png) ; таким образом,
; таким образом,
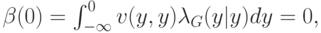
потому что на отрицательных  функция
функция  строго равна нулю; это не слишком замечательно. Но вот при росте
строго равна нулю; это не слишком замечательно. Но вот при росте  происходит интересный эффект.
происходит интересный эффект.
Теорема 11.3. В предположениях теоремы 11.2 при росте значения сигнала  значения ставки в равновесной стратегии возрастают неограниченно:
значения ставки в равновесной стратегии возрастают неограниченно:

Доказательство. Выберем такой  , для которого
, для которого  . Оценим снизу значение
. Оценим снизу значение 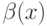 :
:
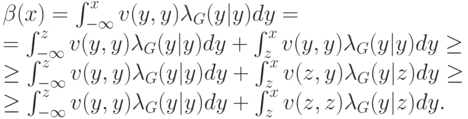
Здесь первое неравенство следует из того, что  возрастает, а второе — из того, что возрастает
возрастает, а второе — из того, что возрастает  .
.
Заметим, что для всех 
![\lambda_G(y|z) = -\frac{d}{dy}\left[\vphantom{1^2}\ln(1-G(y|z))\right],](/sites/default/files/tex_cache/d22f467c8ed6e530d848721f326f76cb.png)
и это значит, что

Теперь подставим это выражение в оценку на  :
:

Но при 
 стремится к единице, а числитель дроби к нулю при этом отнюдь не стремится. Следовательно,
стремится к единице, а числитель дроби к нулю при этом отнюдь не стремится. Следовательно,  .
.
Итак, мы подробно рассмотрели важный и интересный пример аукциона, в котором мало того что платят все, так еще и каждый рад ставить до бесконечности много, если сигнал его приближается к верхней границе (заметим, что при этом ценность лота отнюдь не стремится к бесконечности!).
В следующем параграфе мы разработаем общую технику, которая позволит нам справляться с такого рода аукционами. Это будет последний важный результат в нашем курсе.

